









试读已结束,还剩3页未读,您可下载完整版后进行离线阅读
《2015泉州五校高中毕业班摸底联考数学(文科)试卷+答案》是由用户上传到老师板报网,本为文库资料,大小为347.5 KB,总共有13页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 13页
- 347.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2015年秋季南侨中学、永春三中、永春侨中、荷山中学、南安三中高中毕业班摸底统一考试文科数学试题考生注意:1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.2.请将各题答案填在试卷后面的答题卡上.3.参考公式:锥体的侧面积:lcs底面周长侧21;柱体的侧面积:lcs底面周长侧锥体的表面积:;底面积侧表面积sss柱体的表面积:;底面积侧表面积sss2锥体的体积公式:13VSh;柱体的体积公式:V=Sh,其中S为底面面积,h为高第I卷(选择题共60分)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合|33,|1AxxBxx,则集合AB为()A.[0,3)B.[1,3)C.(1,3)D.(-3,1]2.在复平面内,复数21ii对应的点的坐标为()A.(-1,1)B.(1,1)C.(1,-1)D.(-1,-1)3.下列有关命题的说法正确的是()A.命题“,xR,均有210xx”的否定是:“xR,使得210xx”B.“3x”是“22730xx”成立的充分不必要条件C.线性回归方程axbyˆˆˆ对应的直线一定经过其样本数据点1122,,,,,,nnxyxyxy中的一个点D.若“pq”为真命题,则“pq”也为真命题4.已知,abR,且ba,则()A.22baB.1abC.lg()0abD.11()()22ab211俯视图侧视图正视图135.已知,2,3sin5,则tan4等于()A.-7B.-71C.7D.716.某四棱锥的底面为正方形,其三视图如图所示,则该四棱锥的体积等于()A.1B.2C.3D.47.已知双曲线)0,0(12222babyax的离心率为26,则此双曲线的渐近线方程为()A.2yxB.2yxC.xy22D.12yx8.函数21logfxxx的零点所在的区间为()A.0,1B.1,2C.2,3D.3,49.程序框图如图所示:如果上述程序运行的结果S=1320,那么判断框中应填入( )A.K<10? B.K≤10?C.K<9? D.K≤11?10.已知函数cos,0,2fxxx有两个不同的零点12,xx,且方程0fxmm有两个不同的实根34,xx,若把这四个数按从小到大排列构成等差数列,则实数m=( )A.B.-C.D.-11.在平面区域002xyxy内随机取一点,则所取的点恰好落在圆221xy内的概率是()A.2B.4C.8D.1612.若曲线C上存在点M,使M到平面内两点5,0A,5,0B距离之差的绝对值为8,则称曲线C为“好曲线”.以下曲线不是“好曲线”的是()A.5xy B.229xy C.221259xy D.216xy第Ⅱ卷(非选择题共90分)二.填空题(本题共4小题,每小题4分,共16分,将答案填在题后的横线上.)13.如图是甲、乙两名篮球运动员2013年赛季每场比赛得分的茎叶图,则甲、乙两人比赛得分的中位数之和为.14.已知函数()fx满足11f且(1)2()fxfx,则(1)(2)(10)fff…=15.圆心在曲线3(0)yxx上,且与直线3430xy相切的面积最小的圆的方程是_16.如右图,在直角梯形ABCD中,3,2,,//ABDCADABADDCAB,点M是梯形ABCD内或边界上的一个动点,点N是DC边的中点,则ANAM的最大值是________三.解答题:本题共6小题,满分70分。解答须写出文字说明,证明过程和演算步骤。17.(本小题满分12分)在等差数列na中,nS为其前n项和)(Nn,且243,16aS(Ⅰ)求数列na的通项公式;(Ⅱ)设11nnnaab,求数列nb的前n项和nT.18.(本小题满分12分)已知函数213sincoscos2fxxxx(Ⅰ)求函数fx的最小正周期T;(Ⅱ)把fx的图像向左平移12个单位,得到的图像对应的函数为gx,求函数gx在0,4的取值范围。19.(本小题满分12分)如图,在三棱柱111ABCABC中,1BB平面111ABC,1111ABAC,点D、F分别是棱BC、1CC上的中点,点E是1CC上的动点甲乙7126282319645312NMDCBA(Ⅰ)证明:1//AF平面ADE;(Ⅱ)证明:1AFDE;20.(本小题满分12分)某区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.(Ⅰ)完成下列22列联表,并分析能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?不常吃零食常吃零食总计不患龋齿患龋齿总计(Ⅱ)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.附:))()()(()(22dbcadcbabcadnk21.(本小题满分12分)已知椭圆22221(0)xyabab的长轴长为4,且点3(1,)2在椭圆上.(Ⅰ)求椭圆的方程;(Ⅱ)过椭圆右焦点斜率为k的直线l交椭圆于,AB两点,若0OAOB,求直线l的方程22.(本小题满分14分)已知函数122ln0fxaxaxax.(Ⅰ)当0a时,求fx的极值;(Ⅱ)当0a时,讨论fx的单调性;(Ⅲ)若对任意122,3,,1,3axx,恒有12ln32ln3mafxfx成立,求实数)(02kKP0.0100.0050.0010k6.6357.87910.828m的取值范围。2015年秋季南侨中学、永春三中、永春侨中、荷山中学、南安三中高中毕业班摸底统一考试文科数学试题答题卡班级姓名座号一.选择题:本题共12小题,每小题5分,共60分.在每小题出的四个选项中,只有一项是符合题目要求的.123456789101112CABDABCBADBB二.填空题(本题共4小题,每小题4分,共16分,把答案填在题中横线上)13.5414.102315.223(2)()92xy16.6三.解答题(本题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤).17.(本题满分12分)(Ⅰ)设等差数列的公差是d……………1分由已知条件得113,4616,adad……………2分解得11,2,ad……………2分∴21nan.……………1分(Ⅱ)由(Ⅰ)知,21nan,∴111111()(21)(21)22121nnnbaannnn……………3分1211111111(1)()()(1)2335212122121nnnTbbbnnnn……………3分18.(本题满分12分)解:(Ⅰ)213sincoscos2fxxxx=31cos21sin2222xx……………2分=31sin2cos222xx……………1分=sin26x……………2分∴最小正周期T……………1分(Ⅱ)依题意得:sin2sin21263gxxx……………2分0,4x∴52,336x……………1分∴1sin2,132x……………2分∴gx的取值范围为1,12……………1分19.(本题满分12分)(Ⅰ)证明:连结DF在三棱柱111ABCABC中,点D、F分别是棱BC、1CC上的中点1BDBF平行且等于四边形1BDFB是平行四边形………………………2分1BBDF平行且等于11BBAA平行且等于四边形1AAFD是平行四边形1//AFAD…………………………2分又1AFADEADADE平面平面1//AF平面ADE.…………………………2分(Ⅱ)证明:由1BB平面111ABC,又1AF平面111ABC,所以1BB1AF……2分在三角形111ABC中,1111ABAC,且F为11BC的中点,所以11BC1AF…………2分又1BB111BCB,所以1AF平面11BCCB.又点D、E分别是棱BC、1CC上的点,所以DE平面11BCCB,所以1AFDE.……………………………………2分20.(本题满分12分)解:(Ⅰ)由题意可得列联表:不常吃零食常吃零食总计不患龋齿60100160患龋齿140500640总计200600800注:列联表正确是3分因为828.10667.16600200640160)14010050060(80022k。注:此步正确2分所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系。注:此结论正确1分(Ⅱ)设其他工作人员为丙和丁,4人分组的所有情况有:收集数据:甲乙;甲丙;甲丁;乙丙;乙丁;丙丁;处理数据:丙丁;乙丁;乙丙;甲丁;甲丙;甲乙共有6种。………3分记事件A:工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组………1分则满足条件的情况有:甲丙收集数据,乙丁处理数据;甲丁收集数据,乙丙处理数据共计2种………1分所以2163PA。………1分21.(本题满分12分)解:(Ⅰ)由题意2a.所求椭圆方程为22214xyb.又点3(1,)2在椭圆上,可得1b.所求椭圆方程为2214xy.………4分(Ⅱ)由(Ⅰ)知224,1ab,所以3c,椭圆右焦点为(3,0).则直线AB的方程为(3)ykx.……..1分由22(3),440,ykxxy可得2222(14)831240kxkxk. ………1分由于直线AB过椭圆右焦点,可知0.……..1分设1122(,),(,)AxyBxy,则2212122283124,1414kkxxxxkk,222121212122(3)(3)[3()3]14kyykxxkxxxxk.………2分所以2221212222124114()141414kkkOAOBxxyykkk.……..1分由0OAOB,即22114014kk,可得24211,1111kk.……….1分所以直线l的方程为211(3)11yx. ………1分22.(本题满分14分)解:(1)当0a时,221121-2()2ln()=-=(0)xfxxfxxxxxx、由21-2()=0xfxx、,解得12x,可知fx在10,2上是增函数,在1,2上是减函数.∴fx的极大值为1()2ln222f,无极小值.………………4分2221112(2)1(2)()2(2)ln()=2(2)axaxfxaxaxfxaaxxxx、………………1分.①当02a时,fx在10,2和1,a上是增函数,在11,2a上是减函数;………………1分②当2a时,fx在0,上是增函数;………………1分③当2a时,fx在10,a和1,2上是增函数,在11,2a上是减函数………………1分(3)当23a时,由(2)可知fx在1,3上是增函数,∴323ln241321aaffxfxf.………………2分由12(ln3)2ln3()()mafxfx对任意的3,1,,3.221xxa恒成立,∴12max(ln3)2ln3()()mafxfx………………2分即323ln243ln23lnaaam对任意23a恒成立,即am324对任意23a恒成立,………………1分由于当23a时313324938a,∴313m.………………1分










 苏教版三年级数学下册《3.图形与几何和统计与概率》测试卷word版+(答案)
苏教版三年级数学下册《3.图形与几何和统计与概率》测试卷word版+(答案) 2010年全国统一高考数学试卷(理科)(大纲版ⅱ)+(答案解析)
2010年全国统一高考数学试卷(理科)(大纲版ⅱ)+(答案解析) 2011山东省高考(理科)数学试卷
2011山东省高考(理科)数学试卷 2016年山东省高考数学试卷(理科)word版试卷+答案解析
2016年山东省高考数学试卷(理科)word版试卷+答案解析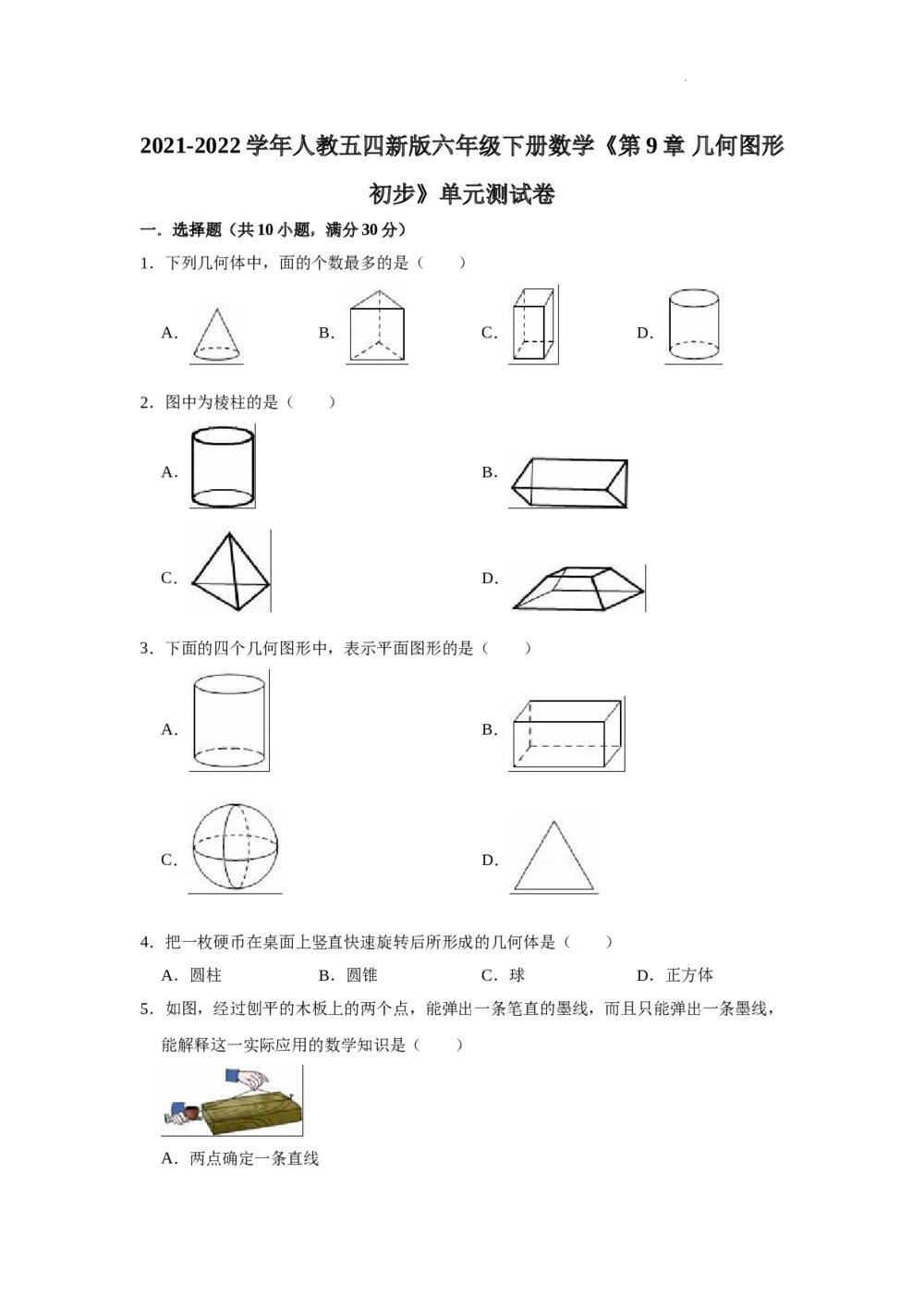 2021-2022学年人教版(五四制)六年级下册数学《第9章几何图形初步》单元测试卷+(含参考答案)
2021-2022学年人教版(五四制)六年级下册数学《第9章几何图形初步》单元测试卷+(含参考答案) 2022-2023学年人教新版七年级数学上册《第4章 几何图形初步》单元测试卷Word版+参考答案
2022-2023学年人教新版七年级数学上册《第4章 几何图形初步》单元测试卷Word版+参考答案