









试读已结束,还剩11页未读,您可下载完整版后进行离线阅读
《2008年上海高考数学(理科)真题试卷+(word解析版)》是由用户上传到老师板报网,本为文库资料,大小为794.5 KB,总共有21页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 21页
- 794.5 KB
- VIP模板
- doc
- 数字产品不支持退货
得分评卷人绝密★启用前2008年普通高等学校招生全国统一考试(上海卷)数学试卷(理工农医类)(满分150分,考试时间120分钟)考生注意1.本场考试时间120分钟,试卷共4页,满分150分,答题纸共2页.2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名,将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4.用2B铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一.填空题(本大题满分44分)本大题共有11题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.1.不等式的解集是.2.若集合、满足,则实数=_____________.3.若复数满足(是虚数单位),则=_____________.4.若函数的反函数为(),则.5.若向量、满足,,且与的夹角为,则=__________.6.函数的最大值是.7.在平面直角坐标系中,从六个点:、、、、、中任取三个,这三点能构成三角形的概率是(结果用分数表示).8.设函数是定义在上的奇函数.若当时,,则满足的的取值范围是.9.已知总体的各个体的值由小到大依次为2,3,3,7,,,12,13.7,18.3,20,且总体的中位数为.若要使该总体的方差最小,则的取值分别是得分评卷人.10.某海域内有一孤岛.岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为、短轴长为的椭圆.已知岛上甲、乙导航灯的海拔高度分别为,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上.现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为,那么船只已进入该浅水区的判别条件是.11.方程的解可视为函数的图像与函数的图像交点的横坐标.若方程的各个实根所对应的点()(=)均在直线的同侧,则实数的取值范围是.二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论是否都写在圆括号内),一律得零分.12.组合数恒等于[答]()(A).(B).(C).(D).13.给定空间中的直线及平面.条件“直线与平面内无数条直线都垂直”是“直线与平面垂直”的[答]()(A)充要条件.(B)充分非必要条件.(C)必要非充分条件.(D)既非充分又非必要条件.14.若数列是首项为1,公比为的无穷等比数列,且各项的和为,则的值是[答]()(A)1.(B)2.(C).(D).15.如图,在平面直角坐标系中,是一个与轴的正半轴、轴的正半轴分别相切于点、的定圆所围成的区域(含边界),是该得分评卷人圆的四等分点.若点、点满足且,则称优于.如果中的点满足:不存在中的其它点优于,那么所有这样的点组成的集合是劣弧[答]()(A).(B).(C).(D).三.解答题(本大题满分90分)本大题共有6题,解答下列各题必须写出必要的步骤.16.(本题满分12分)如图,在棱长为2的正方体中,的中点.求直线与平面所成角的大小(结果用反三角函数值表示).[解]ABBCCDDA得分评卷人17.(本题满分13分)如图,某住宅小区的平面图呈圆心角为的扇形.小区的两个出入口设置在点及点处,且小区里有一条平行于的小路.已知某人从沿走到用了10分钟,从沿走到用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径的长(精确到1米).[解]得分评卷人18.(本题满分15分)本题共有2个小题,第1小题满分6分,第2小题满分9分.已知双曲线,是上的任意点.(1)求证:点到双曲线的两条渐近线的距离的乘积是一个常数;(2)设点的坐标为,求的最小值.[证明](1)[解](2)得分评卷人19.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.已知函数.(1)若,求的值;(2)若对于恒成立,求实数的取值范围.[解](1)(2)得分评卷人20.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分.设是平面直角坐标系中的点,是经过原点与点的直线.记是直线与抛物线的异于原点的交点.(1)已知.求点的坐标;(2)已知点在椭圆上,.求证:点落在双曲线上;(3)已知动点满足,.若点始终落在一条关于轴对称的抛物线上,试问动点的轨迹落在哪种二次曲线上,并说明理由.[解](1)[证明](2)[解](3)得分评卷人21.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分8分.已知以为首项的数列满足:(1)当,时,求数列的通项公式;(2)当,时,试用表示数列前100项的和;(3)当(是正整数),,正整数时,求证:数列,,,成等比数列当且仅当.[解](1)(2)[证明](3)2008年全国普通高等学校招生统一考试上海数学试卷(理工农医类)答案要点及评分标准说明1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.解答一、(第1题至第11题)1..2..3..4..5..6.2.7..8..9..10..11..二、(第12题至第15题)题号12131415代号DCBD三、(第16题至第21题)16.[解]过作,交于,连接.,是直线与平面所成的角.……4分由题意,得.,.……8分,.……10分故直线与平面所成角的大小是.……12分17.[解法一]设该扇形的半径为米.连接.……2分由题意,得=500(米),=300(米),.……4分在△中,,……6分即,……9分解得(米).答:该扇形的半径的长约为445米.……13分[解法二]连接,作,交于.……2分由题意,得=500(米),=300(米),.……4分在△中,,(米),……6分.……9分在直角△中,(米),,(米).答:该扇形的半径的长约为445米.……13分18.[解](1)设是双曲线上任意一点,该双曲线的两条渐近线方程分别是和.……2分点到两条渐近线的距离分别是和,……4分它们的乘积是.点到双曲线的两条渐近线的距离的乘积是一个常数.……6分(2)设的坐标为,则……8分.……11分,……13分当时,的最小值为,即的最小值为.……15分19.[解](1)当时,;当时,.……2分由条件可知,即,解得.……6分,.……8分(2)当时,,……10分即.,.……13分,故的取值范围是.……16分20.[解](1)当时,解方程组得即点的坐标为.……3分[证明](2)由方程组得即点的坐标为.……5分是椭圆上的点,即,.因此点落在双曲线上.……8分(3)设所在抛物线的方程为,.……10分将代入方程,得,即.……12分当时,,此时点的轨迹落在抛物线上;当时,,此时点的轨迹落在圆上;当且时,,此时点的轨迹落在椭圆上;当时,,此时点的轨迹落在双曲线上.……16分21.[解](1)由题意得.……3分(2)当时,,,,,,,…,,,,………6分.……10分(3)当时,;,;,;,.,,,.综上所述,当时,数列,,,是公比为的等比数列.……13分当时,,,,.……15分由于,,,故数列,,,不是等比数列.所以,数列,,,成等比数列当且仅当.……18分1.不等式的解集是 .【答案】【解析】由.2.若集合A={x|x≤2}、B={x|x≥a}满足A∩B={2},则实数a= .【答案】【解析】由.3.若复数z满足z=i(2-z)(i是虚数单位),则z= .【答案】【解析】由.4.若函数f(x)的反函数为f-1(x)=x2(x>0),则f(4)= .【答案】【解析】令.5.若向量\\s\\up6(()、\\s\\up6(()满足|\\s\\up6(()|=1,|\\s\\up6(()|=2,且\\s\\up6(()与\\s\\up6(()的夹角为,则|\\s\\up6(()+\\s\\up6(()|= .【答案】【解析】.6.函数f(x)=sinx+sin(+x)的最大值是 .【答案】【解析】由.7.在平面直角坐标系中,从六个点:A(0,0)、B(2,0)、C(1,1)、D(0,2)、E(2,2)、F(3,3)中任取三个,这三点能构成三角形的概率是 (结果用分数表示).【答案】【解析】已知六个无共线的点生成三角形总数为:;可构成三角形的个数为:,所以所求概率为:;8.设函数f(x)是定义在R上的奇函数,若当x∈(0,+∞)时,f(x)=lgx,则满足f(x)>0的x的取值范围是 .【答案】【解析】由f(x)为奇函数得: 9.已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5,若要使该总体的方差最小,则a、b的取值分别是 .【答案】【解析】根据总体方差的定义知,只需且必须时,总体方差最小;10.某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a,短轴长为2b的椭圆,已知岛上甲、乙导航灯的海拔高度分别为h1、h2,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上,现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为θ1、θ2,那么船只已进入该浅水区的判别条件是 .【答案】【解析】依题意,;11.方程x2+x-1=0的解可视为函数y=x+的图像与函数y=的图像交点的横坐标,若x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi,)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .【答案】【解析】方程的根显然,原方程等价于,原方程的实根是曲线与曲线的交点的横坐标;而曲线是由曲线向上或向下平移个单位而得到的。若交点(xi,)(i=1,2,…,k)均在直线y=x的同侧,因直线y=x与交点为:;所以结合图象可得: ;12.组合数C(n>r≥1,n、r∈Z)恒等于() A.C B.(n+1)(r+1)CC.nrCD.C【答案】【解析】由.13.给定空间中的直线l及平面,条件“直线l与平面内无数条直线都垂直”是“直线l与平面垂直”的()条件A.充要B.充分非必要C.必要非充分D.既非充分又非必要【答案】【解析】直线与平面内的无数条平行直线垂直,但该直线未必与平面垂直,即充分性不成立;14.若数列{an}是首项为1,公比为a-的无穷等比数列,且{an}各项的和为a,则a的值是() A.1B.2C.D.【答案】【解析】由.15.如图,在平面直角坐标系中,是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、P’(x’,y’)满足x≤x’且y≥y’,则称P优于P’,如果中的点Q满足:不存在中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧() A.ABB.BCC.CDD.DA【答案】【解析】依题意,在点Q组成的集合中任取一点,过该点分别作平行于两坐标轴的直线,构成的左上方区域(权且称为“第二象限”)与点Q组成的集合无公共元素,这样点Q组成的集合才为所求.检验得:D.DA xyO·BAC··D·










 新北师大版小学一年级下册数学第一单元精品试卷有答案
新北师大版小学一年级下册数学第一单元精品试卷有答案 2020年高考江苏省数学试卷(原卷word版)
2020年高考江苏省数学试卷(原卷word版) 高中数学《3·4向量在立体几何中的应用》测试卷word版+(含参考答案)
高中数学《3·4向量在立体几何中的应用》测试卷word版+(含参考答案)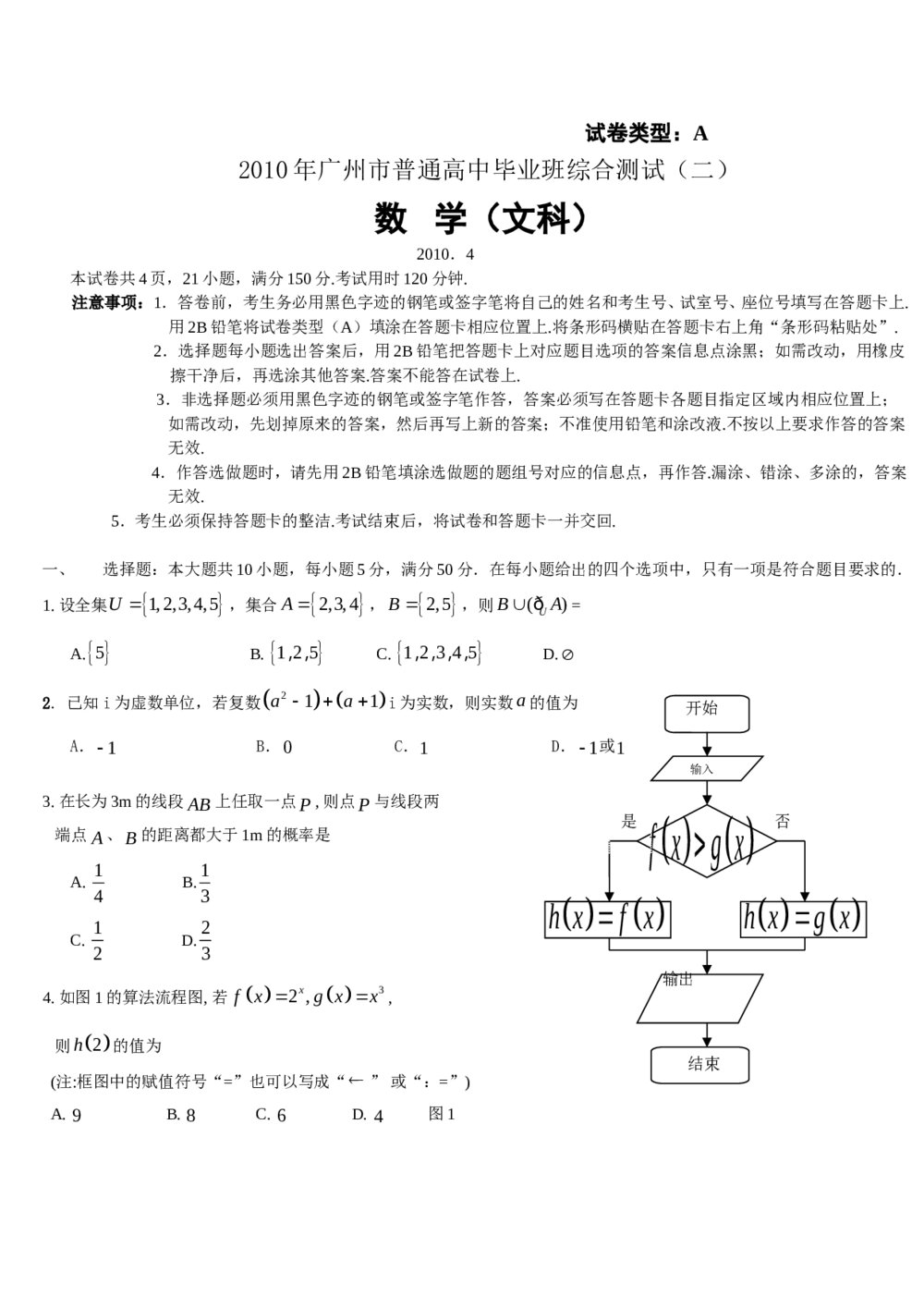 广州市高三二模数学(文科)试题+参考答案
广州市高三二模数学(文科)试题+参考答案 2011年高考一轮课时训练(理)5.2同角三角函数的基本关系及诱导公式+参考答案(通用版)
2011年高考一轮课时训练(理)5.2同角三角函数的基本关系及诱导公式+参考答案(通用版) 2019年高考理科数学试题试卷(天津卷)+参考答案
2019年高考理科数学试题试卷(天津卷)+参考答案