









试读已结束,还剩23页未读,您可下载完整版后进行离线阅读
《高中数学《3·4向量在立体几何中的应用》测试卷word版+(含参考答案)》是由用户上传到老师板报网,本为文库资料,大小为4.32 MB,总共有33页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 33页
- 4.32 MB
- VIP模板
- doc
- 数字产品不支持退货
3.4向量在立体几何中的应用测试卷一、单选题1.设为直线的一个方向向量,为平面的一个法向量,则“”是“”的( )A.充分非必要条件B.必要非充分条件C.充要条件D.非充分非必要条件2.若点,在直线l上,则直线l的一个方向向量为( )A.B.C.D.3.如图,在四棱锥中,底面是矩形,,为棱的中点,且,,若点到平面的距离为,则实数的值为( )A.B.C.D.4.若平面的法向量为,直线l的方向向量为,直线l与平面的夹角为,则下列关系式成立的是( )A.B.C.D.5.已知点,,则直线的一个方向向量可以为( )A.B.C.D.6.在正方体中,,分别为,的中点,则( )A.平面B.异面直线与所成的角为30°C.平面平面D.平面平面7.在棱长为2的正方体中,M,N两点在线段上运动,且,给出下列结论:①在M,N两点的运动过程中,⊥平面;②在平面上存在一点P,使得平面;③棱锥的体积为定值;④以点D为球心作半径为的球面,则球面被正方体表面所截得的所有弧长和为.其中正确结论的序号是( )A.①②③B.①③④C.②④D.②③④8.如图,在棱长为2的正方体中,M,N分别是棱,的中点,点P在线段CM上运动,给出下列四个结论错误的是( )A.平面CMN截正方体ABCD—所得的截面图形是五边形B.直线到平面CMN的距离是;C.存在点P,使得D.△面积的最小值是.二、多选题9.在棱长为的正方体中,则( )A.平面B.直线平面所成角为45°C.棱锥的体积是正方体体积的D.点到平面的距离为10.如图,在棱长为1的正方体中,O为面的中心,E、F分别为BC和的中点,则( )A.平面B.平面与平面相交C.点О到直线的距离为D.点O到平面的距离为11.给出下列命题,其中正确的命题是( )A.若直线的方向向量为,平面的法向量为,则直线B.若对空间中任意一点,有,则四点共面C.两个非零向量与任何一个向量都不能构成空间的一个基底,则这两个向量共线D.已知向量,,则在上的投影向量为12.已知空间中三点,,,则下列结论正确的有( )A.与共线且同向的单位向量是B.C.与夹角的余弦值是D.平面的一个法向量是三、填空题13.已知是直线的一个方向向量,是平面的一个单位法向量,且,则向量的坐标为______.14.已知平面的法向量为,直线l的方向向量为,且,则实数_________.15.在棱柱中,底面为棱长为1的正三角形,侧棱底面,点在棱上,且,则与平面所成的角的正弦值为__________.16.在如图所示的试验装置中,四边形框架为正方形,为矩形,且,且它们所在的平面互相垂直,为对角线上的一个定点,且,活动弹子在正方形对角线上移动,当取最小值时,活动弹子到直线的距离为___________.四、解答题17.已知为直线l的方向向量,为平面的法向量,且,判断直线l与平面的位置关系是平行还是垂直.(1),;(2),.18.如图,在空间直角坐标系中有长方体,且,,,求直线与平面所成角的正弦值.19.如图,在棱柱中,侧面为正方形,,,点在线段上,平面.(1)求证:为的中点;(2)求二面角的大小;(3)在线段上是否存在点,使得直线与平面所成的角为,若存在,求出的值;若不存在,请说明理由.20.如图,正方形ABCD所在平面外一点P满足PB⊥平面ABCD,且AB=3,PB=4.(1)求点A到平面PCD的距离;(2)线段BP上是否存在点E,使得DE⊥平面PAC,若存在,求出该点位置,若不存在,则说明理由.21.如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,,PD⊥底面ABCD,,E是PC的中点,F是PB上的点,且.(1)证明:PD//平面AEF;(2)求二面角的正弦值;(3)求棱锥A-BEF的体积.22.如图①所示,长方形中,,,点是边靠近点的三等分点,将△沿翻折到△,连接,,得到图②的四棱锥.(1)求四棱锥的体积的最大值;(2)设的大小为,若,求平面和平面夹角余弦值的最小值.参考答案1.B【分析】利用空间向量与立体几何的关系即可得到二者的逻辑关系,进而可得“”是“”的必要非充分条件.【详解】为直线的一个方向向量,为平面的一个法向量,则由,可得或,则“”不是“”的充分条件;由,可得,则“”是“”的必要条件.则“”是“”的必要非充分条件.故选:B2.A【分析】由方向向量的概念求解,【详解】由,l的方向向量与平行,只有选项A满足题意,故选:A3.A【分析】先证明平面,以点为原点,,的方向分别为,轴的正方向,建立的空间直角坐标系,利用点到面的距离可求解.【详解】解:由题意得:因为,为中点所以又,与交于点A,平面,平面所以平面以点为原点,,的方向分别为,轴的正方向,建立如图所示的空间直角坐标系,则,,,,故,所以所以又,,设平面的法向量,则令,则,,所以.点到平面的距离为,解得或(舍)故选:A.4.D【分析】由线面角的向量求法判断【详解】由题意得,故选:D5.C【分析】利用空间向量中直线的方向向量的坐标运算求解即可.【详解】解:由题意得:,则直线的方向向量为逐项分析即可知只有C符合要求.故选:C6.D【分析】A项反证法可得;B项由平移法计算异面直线所成角;C项由面面平行的判断和性质可得结果;D项建立空间直角坐标系可得结果.【详解】对于选项A,假设面,则,这与已知与不垂直相矛盾,所以假设不成立.故选项A错误;对于选项B,连接,,因为,所以为异面直线与所成的角或补角,又因为△为等边三角形,所以,故选项B错误;对于选项C,因为,,由面面平行的判定定理可得平面平面,而平面与平面相交,所以平面与平面也相交,故选项C错误;对于选项D,以为坐标原点,,,所在的直线分别为,,轴,建立空间直角坐标系,如图所示,设正方体的棱长为1,则,,,,可得,,,设平面的法向量为,则,可取,则,,即,设平面的法向量为,则,可取,则,,可得平面的一个法向量为,由,所以,即平面平面,故选项D正确.故选:D.7.D【分析】①建立空间直角坐标系,写出点的坐标,当点移动到点时,由于,故与不垂直,所以①错误;②证明出线面平行,从而平面上存在一点P,使得平面;③作出辅助线,利用求出体积为定值;④得到球面被正方体表面所截得的弧为个半径为的圆弧,求出弧长和.【详解】以D为坐标原点,DA所在直线为x轴,DC所在直线为y轴,所在直线为z轴,建立空间直角坐标系,如图1,对于①,当点移动到点时,此时,则,因为,所以与不垂直,所以①错误;对于②,平面与平面为同一个平面,而,所以当点在上时,总有平面,从而有平面,所以②正确;如图3,连接,交于点O,则⊥,故为三角形的高,且,所以,又⊥平面,故,所以③正确;,以点D为球心作半径为的球面,球面被正方体表面所截得的弧为以为圆心,个半径为的圆弧,弧长和为,所以④正确,故选:D.8.D【分析】作出截面图形判断A;由已知可推得平面,先求出以及的面积,利用等积法可判断B;以A点为坐标原点,建立空间直角坐标系,求出相关点的坐标,然后求得利用坐标法可判断C、D.【详解】如图1,直线与、的延长线分别交于,连接分别交于,连接,图1则五边形即为所得的截面图形,故A正确;由题可知,平面,平面,∴平面,故点到平面的距离即为直线到平面的距离,图2设点到平面的距离为h,由正方体的棱长为2可得,,,则,,所以,∴,因为,则,∴由,则,所以,所以直线到平面的距离是,故B正确;如图3,建立空间直角坐标系,则,,,,则.图3设,,∴,又,,,∴,,,假设存在点,使得,∴,整理得,∴(舍去)或,故存在点,使得,故C正确;由上知,所以点在的射影为,∴点到的距离为:,∴当时,,∴故面积的最小值是,故D错误.故选:D.9.AC【分析】建立空间直角坐标系,借助空间向量解决角度距离问题.【详解】正方体中,以为坐标原点,分别以为轴,轴,轴正方向,建立如图所示的空间直角坐标系,则有,.,,,,,得,,由平面,,∴平面,A选项正确;,,设平面的一个法向量,则有,令,得,,则,,所以直线平面所成角不是45°,B选项错误;为边长为的等边三角形,,点到平面的距离,棱锥的体积,而棱长为的正方体的体积为,所以棱锥的体积是正方体体积的,C选项正确;,,设平面的一个法向量,则有,令,得,,则,,点到平面的距离为,故D选项错误.故选:AC10.BC【分析】建系,利用空间向量处理线、面关系以及距离问题.【详解】如图,以为坐标原点建立空间直角坐标系,则有:,设平面的法向量为,由,则,令,则,则,设平面的法向量为,由,则,令,则,则,对A:∵,则,即与不共线,∴不与平面垂直,A错误;对B:∵,则与不共线,∴平面与平面相交,B正确;对C:∵,则,即为锐角,∴,故点О到直线的距离为,C正确;对D:点O到平面的距离为,D错误.故选:BC.11.CD【分析】选项A,因为,直线的方向向量与平面的法向量垂直,直线可能在平面内,也可能与平面平行;选项B,根据空间向量四点共面条件即可判断B;选项C,根据平面向量基底的定义可判断C;选项D,根据投影向量的公式即可判断D.【详解】选项A,由已知直线的方向向量为,平面的法向量为,所以,所以,所以直线或,故A错误;选项B,因为,,根据空间向量四点共面条件可知,四点不共面,故B错误;选项C,三个不共面的向量可以成为空间的一个基底,两个非零向量与任何一个向量都不能构成空间的一个基底,则这两个向量共线,故C正确;选项D,由,,在上的投影向量为,故D正确.故选:CD.12.ABC【分析】首先求出,根据求出与共线且同向的单位向量;验证,可判断B项正误;计算,可判断C项;求出平面的一个法向量,即可判断D项正误.【详解】由已知得,,,.与共线且同向的单位向量是,A项正确;,所以,B项正确;与夹角的余弦值是,C项正确;设平面的一个法向量是,则,即,取,则是平面的一个法向量.设,显然与不共线,所以D项错误.故选:ABC.13.或.【分析】根据线面关系确定与共线的关系,再根据单位向量即可求解.【详解】根据是直线的一个方向向量,,是平面的一个单位法向量,所以与共线,且是单位向量,所以或故答案为:或.14.【分析】根据直线与平面垂直可得直线l的方向向量与平面的法向量平行,利用两向量平行的充要条件即可求解.【详解】因为平面的法向量为,直线l的方向向量为,且,所以,则存在实数使得,也即,解得:,,故答案为:.15.【分析】建立空间直角坐标系,利用空间向量法计算可得.【详解】解:取的中点,连接,过点作,依题意可得,底面,所以底面,如图建立空间直角坐标系,则,,所以,又平面的法向量可以为,设与平面所成的角为,所以,与平面所成的角的正弦值为.故答案为:16.【分析】根据给定条件建立以直线BA,BE,BC分别为x轴,y轴,z轴的空间直角坐标系,利用空间向量即可计算作答.【详解】因为正方形,则,而平面平面,平面平面,于是得平面,又为矩形,即,以射线BA,BE,BC分别为x,y,z轴的非负半轴建立空间直角坐标系,如图,则,因点在上,且,则,又在线段上移动,则有,于是得点,,,因此,当时,取最小值,此时,点,则,,而,则有,,因此,点M到直线BF的距离,所以活动弹子到直线的距离为.故答案为:17.(1)平行(2)垂直【分析】(1)由直线方向向量与平面的法向量垂直,得线面平行;(2)由直线方向向量与平面的法向量平行,得线面垂直.(1),,又,所以.(2),即,所以.18.【分析】求出平面的法向量,用空间向量求解线面角的正弦值.【详解】,,,,,,设平面的法向量为,则,解得:,令得:,则,设直线与平面夹角为,则故直线与平面所成角的正弦值为19.(1)详见解析;(2);(3)存在,或.【分析】(1)设,根据线面平行的性质可得,进而即得;(2)取的中点,根据线面垂直的判定定理可得平面,然后利用坐标法利用面面角的向量求法即得;(3)设,利用线面角的向量求法结合条件即得.【详解】(1)设,连接,因为侧面为正方形,所以为的中点,因为平面,平面,平面平面,所以,又为的中点,所以为的中点;(2)因为,所以,又平面,平面,所以平面,取的中点,则,由平面,平面,可得,又平面,平面,所以平面,如图以为原点建立空间直角坐标系,则,所以,设平面的法向量为,则,令,则,又平面的法向量可取,所以,所以二面角的大小为;(3)假设在线段上存在点,使得直线与平面所成的角为,设,因为,所以,,又,所以,又平面的一个法向量为,所以,整理可得,解得或,所以在线段上存在点,使得直线与平面所成的角为,的值为或.20.(1);(2)不存在,理由见解析.【分析】(1)利用等积法,根据线面垂直,面面垂直的判定及性质结合条件即得;(2)利用坐标法,设,结合条件可得,进而即得.【详解】(1)由题意,,由PB⊥平面ABCD,PB⊂平面PBC,可得平面PBC⊥平面ABCD,而DC⊥BC,且平面平面,平面ABCD,∴DC⊥平面PBC,平面PBC,可得DC⊥PC,∵CD=3,PC=,∴,设A到平面PCD的距离为h,则,即h=,∴点A到平面PCD的距离为;(2)以B为坐标原点,分别以BC、BA、BP所在直线为x、y、z轴建立空间直角坐标系,则D(3,3,0),C(3,0,0),P(0,0,4),设,则,,若DE⊥平面PAC,则,解得,不合题意,故线段BP上不存在点E,使得DE⊥平面PAC.21.(1)证明见详解(2)(3)【分析】(1)建系,利用空间向量证明线面关系;(2)利用空间向量求二面角;(3)先根据空间向量求点到平面的距离,再求棱锥的体积.【详解】(1)连接,由题意可知:为等边三角形,取的中点,连接,则,∵,则,如图,以为坐标原点建立空间直角坐标系,则,可得,设平面的法向量,则,令,则,即,∵,且平面,∴平面.(2)由(1)可得:,设平面的法向量为,则,令,则,即,设平面的法向量为,则,令,则,即,可得,设二面角为,则可得,故二面角的正弦值.(3)由(2)可得:,即为等腰直角三角形,∵点到平面的距离,∴棱锥A-BEF的体积.22.(1)(2)平面和平面夹角余弦值的最小值为【分析】(1)作出辅助线,得到当平面平面时,点到平面的距离最大,四棱锥的体积取得最大值,求出,从而得到体积最大值;(3)作出辅助线,得到为的平面角,即,建立空间直角坐标系,用含的关系式表达出平面和平面的法向量,利用空间向量夹角余弦公式及,得到,结合的取值范围求出余弦值的最小值.【详解】(1)解:取的中点,连接,因为,则,当平面平面时,点到平面的距离最大,四棱锥的体积取得最大值,此时平面,且,底面为梯形,面积为,则四棱锥的体积最大值为;(2)解:连接,因为,所以,所以为的平面角,即,过点作平面,以为坐标原点,分别以,,所在直线为轴,轴,轴,建立如图所示的空间直角坐标系,则,,,过作于点,由题意得平面,设,,,所以,所以,所以,设平面的法向量为,则,令,则,设平面的法向量为,因为,则,令,可得:,设两平面夹角为,则,令,所以,则所以,所以当时,有最小值,所以平面和平面夹角余弦值的最小值为.【点睛】关键点点睛:利用二面角的平面角来表示折叠过程中形成的动点的横、纵、竖坐标,从而减少题中的变量,并且求解平面与平面夹角的余弦值时,两个平面法向量都含参数的正弦或余弦值,利用空间向量的坐标运算求解时,还需应用与的关系进行变形处理,从而使得只含或者的式子,转换成单变量的函数关系从而可以利用函数思想求解的最值,属于较难题目.展开内容










![六年级数学奥数《第五讲[1]几何-立体部分》教师版PPT课件](https://img.banbaow.com/uploadfile/2023/0601/80d687a3965e58674594f/0.jpg) 六年级数学奥数《第五讲[1]几何-立体部分》教师版PPT课件
六年级数学奥数《第五讲[1]几何-立体部分》教师版PPT课件 2011海淀区高三二模数学期末练习试卷(理科)+答案
2011海淀区高三二模数学期末练习试卷(理科)+答案 2019年上海高考数学真题试卷+(答案解析word版)
2019年上海高考数学真题试卷+(答案解析word版)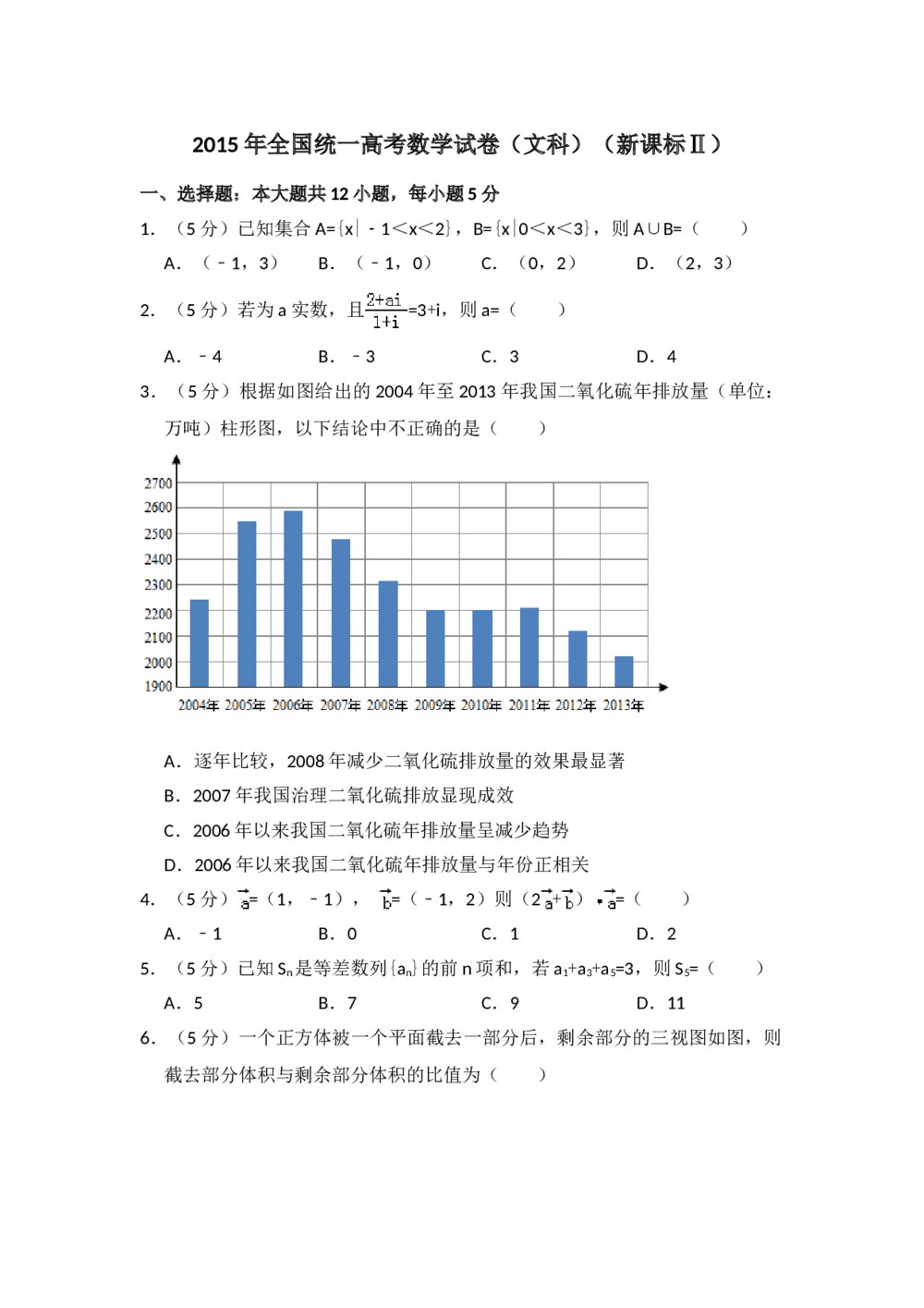 2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析
2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析 人教版小学数学六年级上期末阶段检测(4)+参考答案
人教版小学数学六年级上期末阶段检测(4)+参考答案 人教版数学二年级下册《归类达标测试卷3·几何与统计推理》试题word版+(答案)
人教版数学二年级下册《归类达标测试卷3·几何与统计推理》试题word版+(答案)