









试读已结束,还剩1页未读,您可下载完整版后进行离线阅读
《2012年广东省高考(文科)数学B卷+答案解析》是由用户上传到老师板报网,本为文库资料,大小为456.5 KB,总共有11页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 11页
- 456.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2012年普通高等学校招生全国统一考试(广东卷)B数学(文科)解析【试卷总评】一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1设i为虚数单位,则复数34ii=A-4-3iB-4+3iC4+3iD4-3i2设集合U={1,2,3,4,5,6},M={1,3,5}则UCMA{2,4,6}B{1,3,5}C{1,2,4}D.U3若向量AB=(1,2),BC=(3,4),则AC=A(4,6)B(-4,-6)C(-2,-2)D(2,2)【答案】A【解析】因为AC=AB+BC=(4,6),所以选A.【考点定位】本题考查平面向量的坐标运算(加法),属基础题.4下列函数为偶函数的是Ay=sinxBy=3xCy=xeDy=ln21x【答案】D【解析】观察可得:四个选项的定义域均为R,且只有函数y=ln21x是偶函数,故选D.【考点定位】本题考查函数的性质(奇偶性),属基础题.5.已知变量x,y满足约束条件1110xyxyx,则z=x+2y的最小值为A.3B.1C.-5D.-66.在△ABC中,若∠A=60°,∠B=45°,BC=32,则AC=A.43B.23C.3D.327.某几何体的三视图如图1所示,它的体积为A.72πB.48πC.30πD.24π8.在平面直角坐标系xOy中,直线3x+4y-5=0与圆x²+y²=4相交于A、B两点,则弦AB的长等于A.33B.23C.3D.1【答案】B【解析】因为弦心距为1d,所以弦AB的长等于24123,故选B.【考点定位】本题考查直线与圆相交的位置关系,属中档题.9.执行如图2所示的程序框图,若输入n的值为6,则输出s的值为A.105B.16C.15D.110.对任意两个非零的平面向量α和β,定义.若两个非零的平面向量a和b,满足a与b的夹角,且ab和ba都在集合中,则ab=A.52B.32C.1D.12二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。(一)必做题(11~13题)11.函数的定义域为__________。【答案】[1,0)(0,)【解析】要使函数有意义,须满足10x且0x,解得定义域为[1,0)(0,).【考点定位】本题考查函数的定义域,属容易题.12.若等比数列{an}满足a2a4=,则【答案】14【解析】因为是等比数列,所以21524312aaaaa,所以2135aaa=14.【考点定位】本题考查等比数列的性质,属容易题.13.由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为__________。(从小到大排列)【答案】1,2,2,3【解析】由题意知:x2+x3=4,x1+x4=4,容易得答案.【考点定位】本题考查平均数与中位数及标准差的求解.(二)选做题(14-15题,考生只能从中选做一题)14,(坐标系与参数方程选做题)在平面直角坐标系xOy中,曲线C1和C2的参数方程分别为和,则曲线C1与C2的交点坐标为_______。15.(几何证明选讲选做题)如图3所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA,若AD=m,AC=n,则AB=_________。【答案】mn【解析】由弦切角定理知:∠PBA=∠ACB,又因为∠PBA=∠DBA,所以∠DBA=∠ACB,所以ABDACB,mABABn,解得AB=mn.【考点定位】本题考查三角形相似与弦切角定理.三、解答题:本大题共6小题,满分80分。解答须写出文字说明、证明过程和演算步骤。16.(本小题满分12分)已知函数,x∈R,且.(1)求A的值;(2)设,,,求cos(α+β)的值.17.(本小题满分13分)某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].(1)求图中a的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.18.(本小题满分13分)如图5所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△PAD边上的高.(1)证明:PH⊥平面ABCD;(2)若PH=1,AD=2,FC=1,求三棱锥E-BCF的体积;(3)证明:EF⊥平面PAB.【解析】(1)证明:因为PH为△PAD边上的高,所以PH⊥AD,又因为AB⊥平面PAD,PH平面PAD,所以AB⊥PH,又因为PHAD=H,所以PH⊥平面ABCD;(2)因为E是PB的中点,所以点E到平面BCF的距离d等于点P到平面ABCD距离的一半,即d=12,又因为BCFS12ADCF=22,所以三棱锥E-BCF的体积为212;19.(本小题满分14分)设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N﹡.(1)求a1的值;(2)求数列{an}的通项公式.20.(本小题满分14分)在平面直角坐标系xoy中,已知椭圆C1:22221(0)xyabab的左焦点为F1(-1,0),且点P(0,1)在C1上。(1)求椭圆C1的方程;(2)设直线l同时与椭圆C1和抛物线C2:24yx相切,求直线l的方程.【解析】(1)由题意知:1c,1b,所以22a,故椭圆C1的方程为2212xy.0,整理得:2221mk②,解①②得:22m,即22,2mk或21.(本小题满分14分)设0<a<1,集合(1)求集合D(用区间表示)(2)求函数在D内的极值点.当113a时,集合B=,所以集合D=AB;当13a时,集合B=|1xx,此时集合D=|01xxx且.










 高中高二学科数学《微积分基本定理》测试卷(word版)
高中高二学科数学《微积分基本定理》测试卷(word版) 《广东卷》理科综高考题试卷
《广东卷》理科综高考题试卷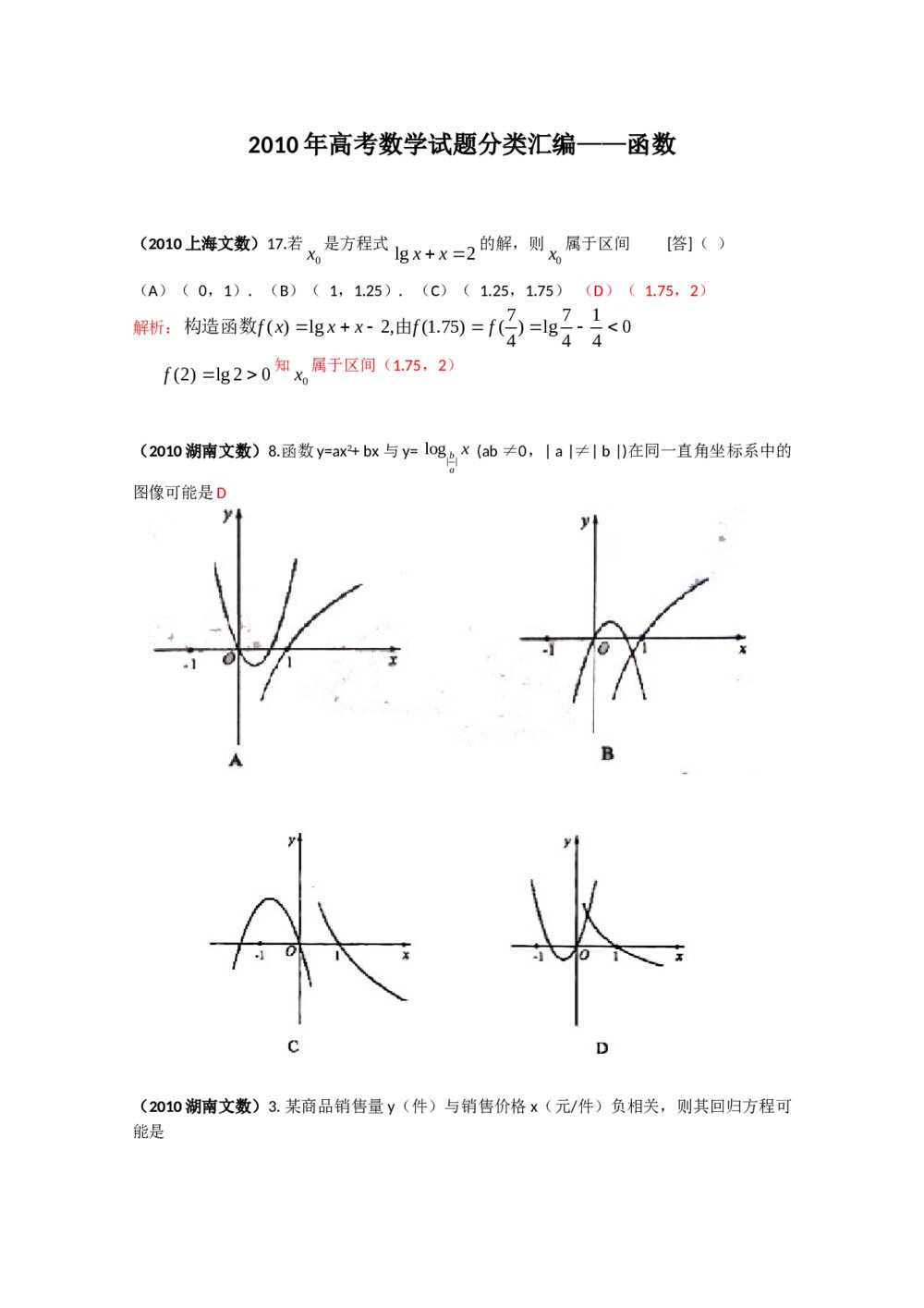 2010年高考数学试题分类汇编--函数+(答案解析)
2010年高考数学试题分类汇编--函数+(答案解析) 2014年天津高考文科数学试题试卷word版+(参考含答案)
2014年天津高考文科数学试题试卷word版+(参考含答案) 高考文科数学二轮专题复习题《数学思想方法和常用的解题技》
高考文科数学二轮专题复习题《数学思想方法和常用的解题技》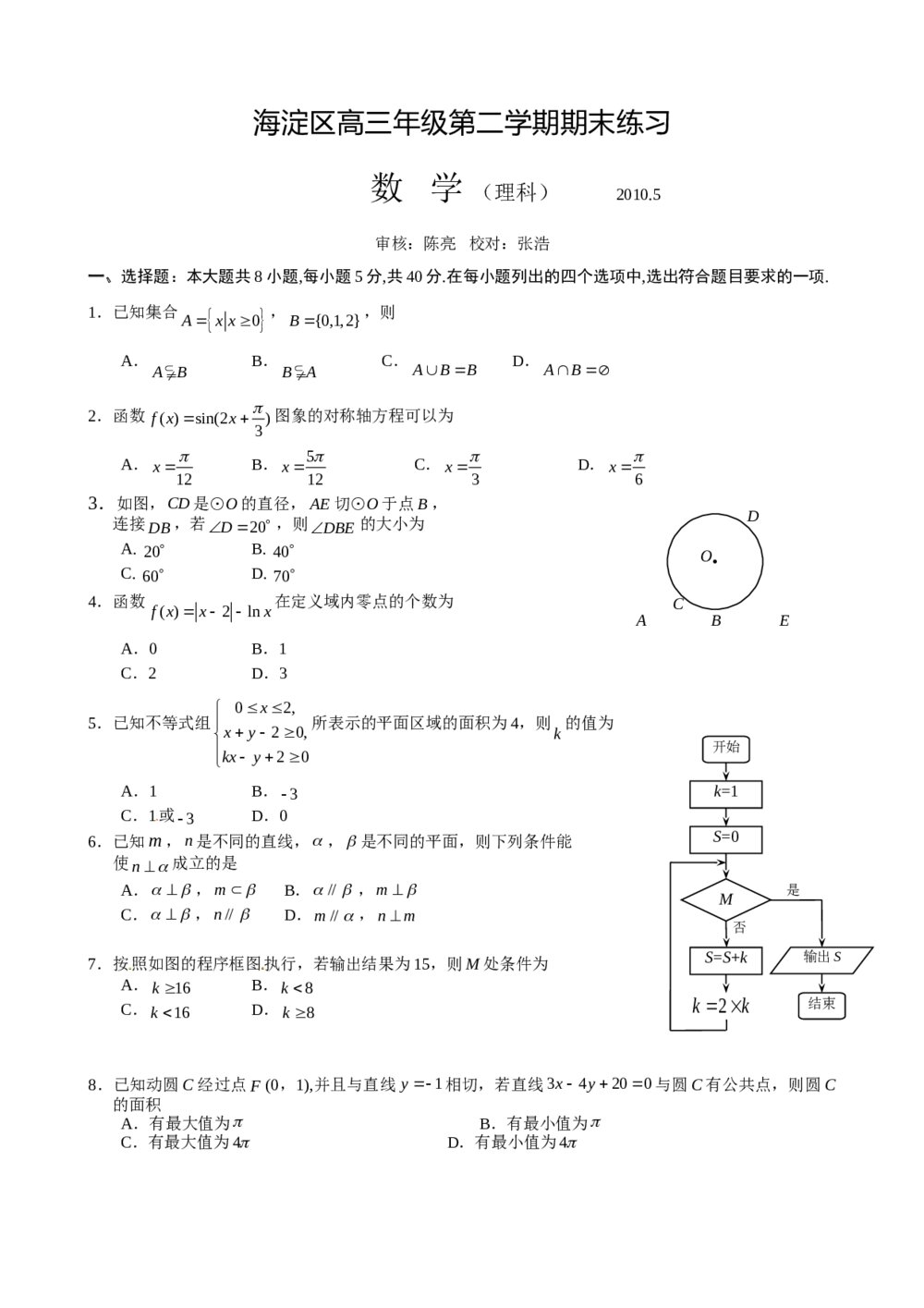 海淀区高三二模数学(理科)试题试卷+参考答案word版
海淀区高三二模数学(理科)试题试卷+参考答案word版