









试读已结束,还剩3页未读,您可下载完整版后进行离线阅读
《2017年高考数学知识方法专题11《数学方法第48练 整体策略与换元法》》是由用户上传到老师板报网,本为文库资料,大小为154 KB,总共有13页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 13页
- 154 KB
- VIP模板
- doc
- 数字产品不支持退货
第48练 整体策略与换元法[题型分析·高考展望] 整体思想是指把研究对象的某一部分(或全部)看成一个整体,通过观察与分析,找出整体与局部的联系,从而在客观上寻求解决问题的新途径.换元法又称辅助元素法、变量代换法,通过引进新的变量,可以把分散的条件联系起来,隐含的条件显露出来;或者把条件与结论联系起来;或者变为熟悉的形式,把复杂的计算和推证简化.高考必会题型题型一 整体策略例1 (1)计算(1----…-)×(++++…+)-(1-----…--)×(+++…+);(2)解方程(x2+5x+1)(x2+5x+7)=7.解 (1)设+++…+=t,则原式=(1-t)(t+)-(1-t-)t=t+-t2-t-t+t2+t=.(2)设x2+5x=t,则原方程化为(t+1)(t+7)=7,∴t2+8t=0,解得t=0或t=-8,当t=0时,x2+5x=0,x(x+5)=0,x1=0,x2=-5;当t=-8时,x2+5x=-8,x2+5x+8=0,Δ=b2-4ac=25-4×1×8<0,此时方程无解;即原方程的解为x1=0,x2=-5.点评 整体是与局部对应的,按常规不容易求某一个(或多个)未知量时,可打破常规,根据题目的结构特征,把一组数或一个代数式看作一个整体,从而使问题得到解决.变式训练1 计算:(1---)×(+++)-(1----)×(++).解 令++=t,则原式=(1-t)(t+)-(1-t-)t=t+-t2-t-t+t2=.题型二 换元法例2 (1)已知函数f(x)=4x-2xt+t+1在区间(0,+∞)上的图象恒在x轴上方,则实数t的取值范围是________________.(2)已知点A是椭圆+=1上的一个动点,点P在线段OA的延长线上,且OA·OP=48,则点P的横坐标的最大值为________.答案 (1)(-∞,2+2) (2)10解析 (1)令m=2x(m>1),则问题转化为函数f(m)=m2-mt+t+1在区间(1,+∞)上的图象恒在x轴上方,即Δ=t2-4(t+1)<0或解得t<2+2,即实数t的取值范围是(-∞,2+2).(2)当点P的横坐标最大时,射线OA的斜率k>0,设OA:y=kx,k>0,与椭圆+=1联立解得x=,又OA·OP=xAxP+k2xAxP=48,解得xP===,令9+25k2=t>9,即k2=,则xP==×25=80≤80×=10,当且仅当t=16,即k2=时取等号,所以点P的横坐标的最大值为10.(3)已知函数f(x)=ax-ln(1+x2).①当a=时,求函数f(x)在(0,+∞)上的极值;②证明:当x>0时,ln(1+x2)g(0)=0,∴ln(1+x2)1),则f(x)的最小值为________.答案 2+2解析 f(x)=+2(x-1)+2,令x-1=t,则f(t)=+2t+2(t>0),∴f(t)≥2+2=2+2.当且仅当=2t时等号成立,故f(x)的最小值为2+2,当且仅当=2(x-1),即x=+1时等号成立.(2)已知在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足S=an.①求Sn的表达式;②设bn=,数列{bn}的前n项和为Tn,证明Tn<.①解 ∵S=an,an=Sn-Sn-1(n≥2),∴S=(Sn-Sn-1),即2Sn-1Sn=Sn-1-Sn,(*)由题意得Sn-1·Sn≠0,(*)式两边同除以Sn-1·Sn,得-=2,∴数列是首项为==1,公差为2的等差数列.∴=1+2(n-1)=2n-1,∴Sn=.②证明 ∵bn===,∴Tn=b1+b2+…+bn=[(1-)+(-)+…+(-)]==<,∴Tn<.高考题型精练1.已知长方体的表面积为11,其12条棱的长度之和为24,则这个长方体的一条对角线长为( )A.2B.C.5D.6答案 C解析 设长方体长,宽,高分别为x,y,z,由已知“长方体的表面积为11,其12条棱的长度之和为24”,得长方体所求对角线长为===5,故选C.2.设实数x,y,m,n满足x2+y2=1,m2+n2=3,那么mx+ny的最大值是______.答案 解析 设x=sinα,y=cosα,m=sinβ,n=cosβ,其中α,β∈(0°,180°),∴mx+ny=sinβsinα+cosβcosα=cos(α-β),故最大值为.3.函数y=3-4的最小值为________.答案 -8解析 由解得-2≤x≤2,所以函数的定义域为[-2,2].因为()2+()2=4,故可设(θ∈[0,]),则y=3×2sinθ-4×2cosθ=6sinθ-8cosθ=10sin(θ-φ)(φ∈(0,),cosφ=,sinφ=),因为θ∈[0,],所以θ-φ∈[-φ,-φ],所以当θ=0时,函数取得最小值10sin(-φ)=10×(-)=-8.4.已知不等式>ax+的解集是(4,b),则a=______,b=________.答案 36解析 令=t,则t>at2+,即at2-t+<0,其解集为(2,),故解得a=,b=36.5.已知y=f(x)为偶函数,当x≥0时,f(x)=-x2+2x,则满足f(f(a))=的实数a的个数为________.答案 8解析 由题意知,f(x)=其图象如图所示,令t=f(a),则t≤1,令f(t)=,解得t=1-或t=-1±,即f(a)=1-或f(a)=-1±,由数形结合得,共有8个交点.6.设f(x2+1)=loga(4-x4)(a>1),则f(x)的值域是________.答案 (-∞,loga4]解析 设x2+1=t(t≥1),∴f(t)=loga[-(t-1)2+4],∴值域为(-∞,loga4].7.已知m∈R,函数f(x)=g(x)=x2-2x+2m-1,若函数y=f(g(x))-m有6个零点,则实数m的取值范围是________.答案 (0,)解析 函数f(x)=的图象如图所示,令g(x)=t,y=f(t)与y=m的图象最多有3个交点,当有3个交点时,02m-2,①又0
展开内容










 揭阳市高考一模试题(数学理科)+参考答案
揭阳市高考一模试题(数学理科)+参考答案 考研数学真题测试卷试题解析(word版)
考研数学真题测试卷试题解析(word版)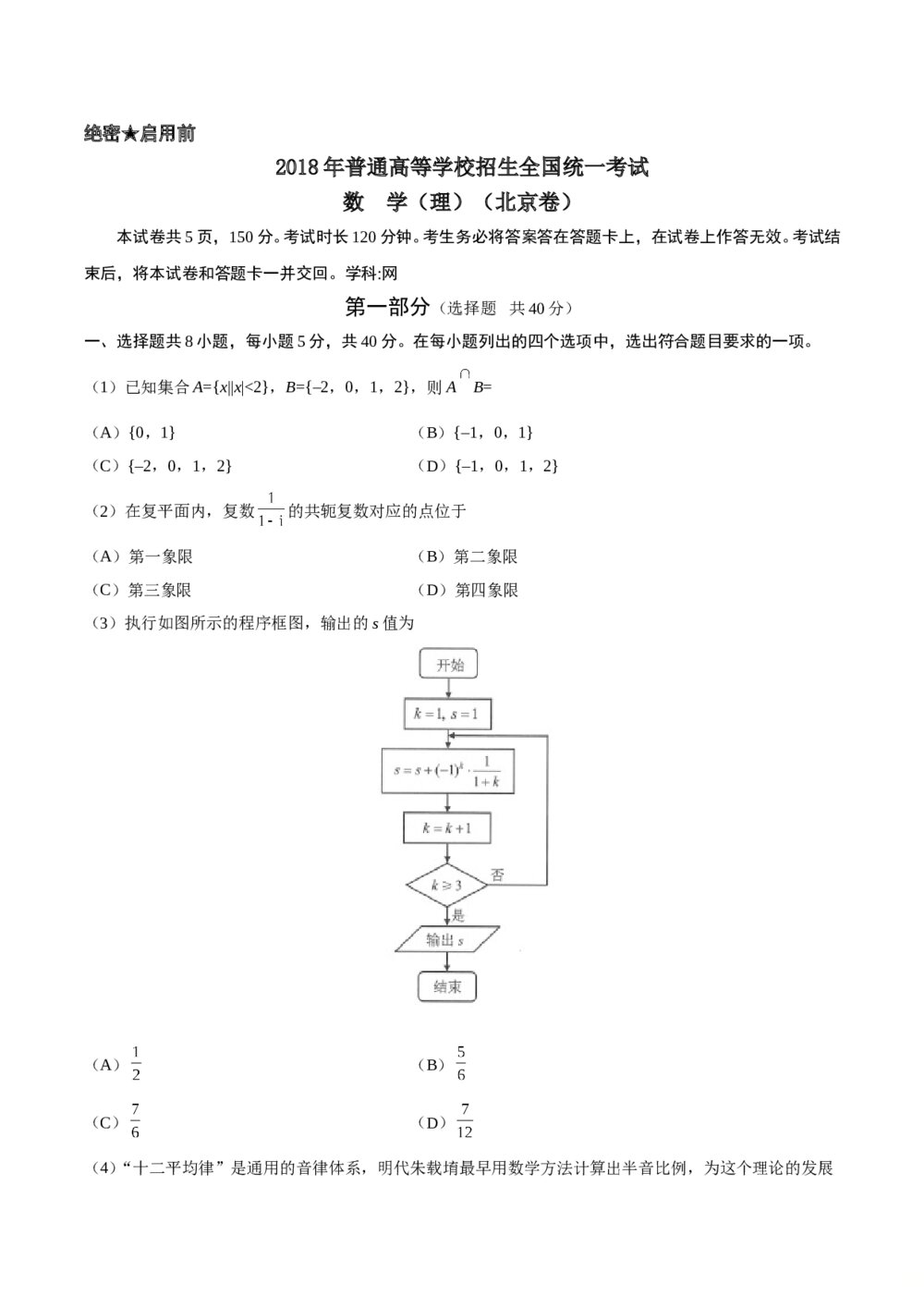 2018年北京高考数学(理科)试题试卷+参考答案
2018年北京高考数学(理科)试题试卷+参考答案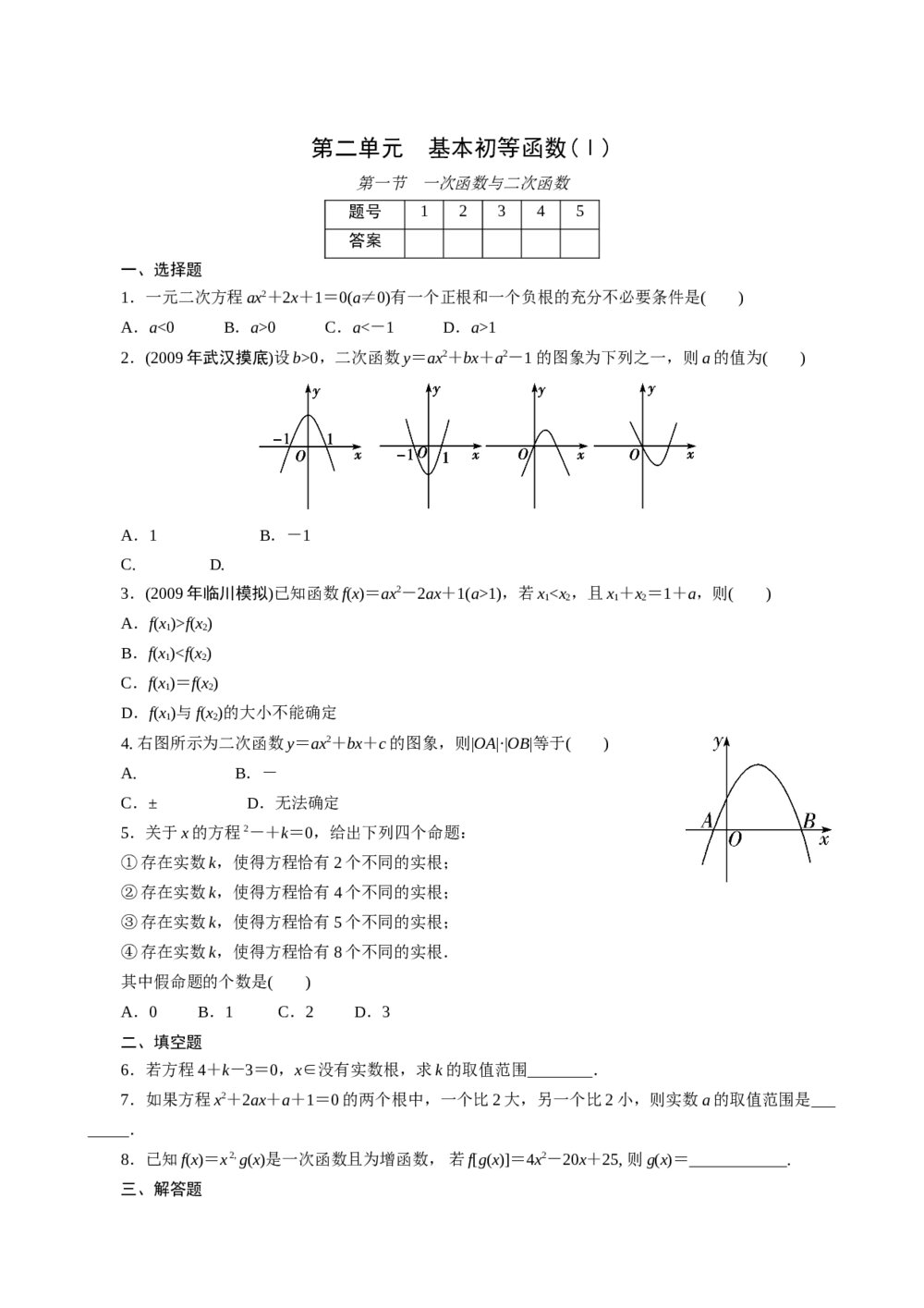 2011年高考一轮课时训练(理)3.2.1一次函数与二次函数+参考答案 (通用版)
2011年高考一轮课时训练(理)3.2.1一次函数与二次函数+参考答案 (通用版) 2020年全国统一高考数学(理科)试卷(新课标Ⅰ)(原卷版)
2020年全国统一高考数学(理科)试卷(新课标Ⅰ)(原卷版) 2015届安庆市五校高三联考数学(理科)试题+参考答案
2015届安庆市五校高三联考数学(理科)试题+参考答案