




《2017年高考理科数学三轮冲刺热点题型 压轴大题突破练(二) 直线与圆锥曲线(2)》是由用户上传到老师板报网,本为文库资料,大小为68.5 KB,总共有5页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 5页
- 68.5 KB
- VIP模板
- doc
- 数字产品不支持退货
压轴大题突破练(二) 直线与圆锥曲线(2)1.(2016·浙江)如图,设椭圆+y2=1(a>1).(1)求直线y=kx+1被椭圆截得的线段长(用a,k表示);(2)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.解 (1)设直线y=kx+1被椭圆截得的线段为AM,由得(1+a2k2)x2+2a2kx=0,故x1=0,x2=-,因此|AM|=|x1-x2|=·.(2)假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q,满足|AP|=|AQ|.记直线AP,AQ的斜率分别为k1,k2,且k1,k2>0,k1≠k2.由(1)知,|AP|=,|AQ|=,故=,所以(k-k)[1+k+k+a2(2-a2)kk]=0.由于k1≠k2,k1,k2>0得1+k+k+a2(2-a2)kk=0,因此=1+a2(a2-2).①因为①式关于k1,k2的方程有解的充要条件是1+a2(a2-2)>1,所以a>.因此,任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点的充要条件为1<a≤,由e==,得00)交于A,B两点,且OA·OB=-3,其中O为坐标原点.(1)求p的值;(2)当|AM|+4|BM|最小时,求直线l的方程.解 (1)设A(x1,y1),B(x2,y2),直线l的方程为x=my+.联立消去x,得y2-2pmy-p2=0.∴y1+y2=2pm,y1y2=-p2.∵OA·OB=-3,∴x1x2+y1y2=-3.又x1x2=·=,∴-p2=-3⇒p2=4.∵p>0,∴p=2.(2)由抛物线定义,得|AM|=x1+=x1+1,|BM|=x2+=x2+1,∴|AM|+4|BM|=x1+4x2+5≥2+5=9,当且仅当x1=4x2时取等号.将x1=4x2代入x1x2==1,得x2=(负值舍去).将x2=代入y2=4x,得y2=±,即点B.将点B代入x=my+1,得m=±.∴直线l的方程为x=±y+1,即4x±y-4=0.3.已知动点S(x,y)到直线l:x=2的距离是它到点T(,0)的距离的倍.(1)求动点S的轨迹C的方程;(2)设轨迹C上一动点P满足:OP=λOM+2μON,其中M,N是轨迹C上的点,直线OM与ON的斜率之积为-,若Q(λ,μ)为一动点,E1(-,0),E2(,0)为两定点,求|QE1|+|QE2|的值.解 (1)点S(x,y)到直线x=2的距离,是到点T(,0)的距离的倍,则|x-2|=,化简得+=1.所以轨迹C的方程为+=1.(2)设P(x,y),M(x1,y1),N(x2,y2),则OP=λOM+2μON,即x=λx1+2μx2,y=λy1+2μy2,因为点P,M,N在椭圆+=1上,所以x+2y=4,x+2y=4,x2+2y2=4,故x2+2y2=λ2(x+2y)+4μ2(x+2y)+4λμ(x1x2+2y1y2)=4λ2+16μ2+4λμ(x1x2+2y1y2)=4,设kOM,kON分别为直线OM,ON的斜率,由题意知,kOM·kON==-,因此x1x2+2y1y2=0,所以λ2+4μ2=1,所以点Q是椭圆λ2+4μ2=1上的点,而E1,E2恰为该椭圆的左,右焦点,所以由椭圆的定义可得,|QE1|+|QE2|=2.4.已知曲线C上任意一点P到两定点F1(-1,0)与F2(1,0)的距离之和为4.(1)求曲线C的方程;(2)设曲线C与x轴负半轴交点为A,过点M(-4,0)作斜率为k的直线l交曲线C于B、C两点(B在M、C之间),N为BC中点.①证明:k·kON为定值;②是否存在实数k,使得F1N⊥AC?如果存在,求直线l的方程,如果不存在,请说明理由.(1)解 由已知可得:曲线C是以两定点F1(-1,0)和F2(1,0)为焦点,长轴长为4的椭圆,所以a=2,c=1⇒b==,故曲线C的方程为+=1.(2)证明 设过点M的直线l的方程为y=k(x+4),设B(x1,y1),C(x2,y2)(x2>x1).①联立方程组得(4k2+3)x2+32k2x+64k2-12=0,则故xN==,yN=k(xN+4)=.所以kON=-,所以k·kON=-为定值.②解 若F1N⊥AC,则kAC·kF1N=-1,因为F1(-1,0),kF1N==,因为A(-2,0),kAC=,故·=-1,代入y2=k(x2+4)得x2=-2-8k2,y2=2k-8k3,而x2≥-2,故只能k=0,显然不成立,所以这样的直线不存在.展开内容





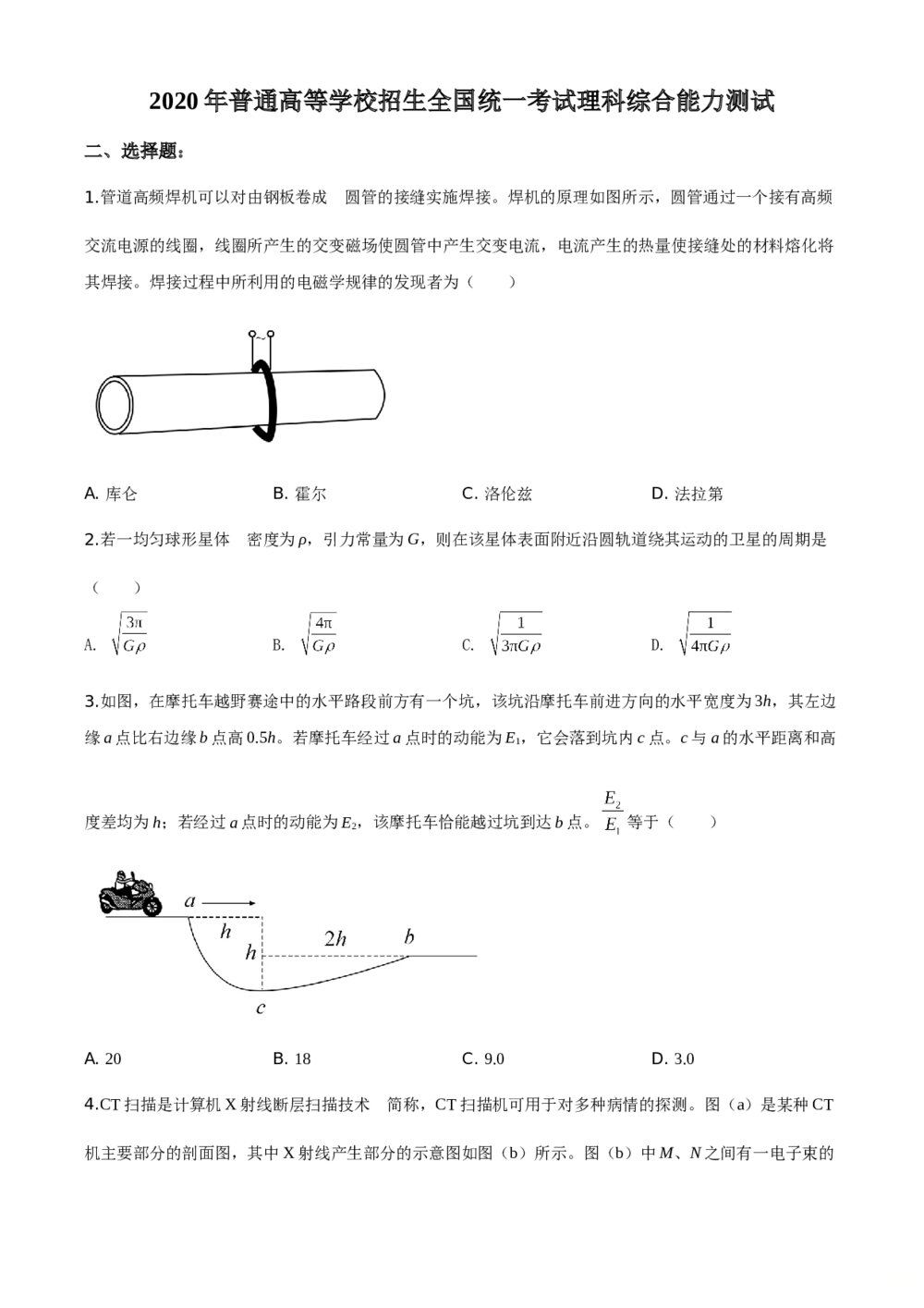 2020年高考全国卷Ⅱ理综能力综合测试试卷(原卷版)
2020年高考全国卷Ⅱ理综能力综合测试试卷(原卷版) 2011海淀高三年级第二学期数学(理科)期中试题练习+答案
2011海淀高三年级第二学期数学(理科)期中试题练习+答案 2011昌平区高三二模(文科)数学试卷+答案
2011昌平区高三二模(文科)数学试卷+答案 2011年高考一轮课时训练(理)11.1.4空间图形的垂直关系+参考答案(通用版)
2011年高考一轮课时训练(理)11.1.4空间图形的垂直关系+参考答案(通用版) 2017年全国统一高考数学试卷(理科)(新课标ⅰ)+参考答案解析
2017年全国统一高考数学试卷(理科)(新课标ⅰ)+参考答案解析 北京市石景山区高三一模数学文科+参考答案
北京市石景山区高三一模数学文科+参考答案