



《2011年高考一轮课时训练(理)11.1.4空间图形的垂直关系+参考答案(通用版)》是由用户上传到老师板报网,本为文库资料,大小为131.5 KB,总共有4页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 4页
- 131.5 KB
- VIP模板
- doc
- 数字产品不支持退货
第四节 空间图形的垂直关系题号12345答案一、选择题1.(2008年安徽卷)已知m、n是两条不同直线,α、β、γ是三个不同平面,下列命题中正确的是( )A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n2.(2009年浙江卷)设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )A.若l⊥α,α⊥β,则l⊂βB.若l∥α,α∥β,则l⊂βC.若l⊥α,α∥β,则l⊥βD.若l∥α,α⊥β,则l⊥β3.(2009年广东卷)给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( )A.①和②B.②和③C.③和④D.②和④4.关于直线m、n与平面α与β,有下列四个命题:①若m∥α,n∥β且α∥β,则m∥n;②若m⊥α,n⊥β且α⊥β,则m⊥n;③若m⊥α,n∥β且α∥β,则m⊥n;④若m∥α,n⊥β且α⊥β,则m∥n;其中真命题的序号是( )A.①② B.③④C.①④ D.②③5.已知两条直线m、n,两个平面α、β,给出下面四个命题①m∥n,m⊥α⇒n⊥α ②α∥β,m⊂α,n⊂β⇒m∥n③m∥n,m∥α⇒n∥α ④α∥β,m∥n,m⊥α⇒n⊥β其中正确命题的序号是( )A.①③ B.②④C.①④ D.②③二、填空题6.下列命题中,设α、β、γ为不同平面,a、b为不同直线,下列命题是真命题的有________.①a⊥α,a⊥β⇒α∥β.②a⊥α,a∥b⇒b⊥α.③α⊥β,a⊂α,b⊂β⇒a⊥b.④a⊥α,a⊥b⇒b∥α.7.设三棱锥P-ABC的顶点P在平面ABC上的射影是H,给出以下命题:①若PA⊥BC,PB⊥AC,则H是△ABC的垂心②若PA、PB、PC两两互相垂直,则H是△ABC的垂心③若∠ABC=90°,H是AC的中点,则PA=PB=PC④若PA=PB=PC,则H是△ABC的外心其中正确命题的命题是________.8.(2009年浙江)如下图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是_____________.三、解答题9.如右图所示,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=.(1)求证:PA⊥平面ABCD;(2)求四棱锥P-ABCD的体积.10.如右图,A、B、C、D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴运动.(1)当平面ADB⊥平面ABC时,求CD;(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.参考答案1.解析:m、n均为直线,其中m、n平行α,m、n可以相交也可以异面,故A不正确;m⊥α,n⊥α则同垂直于一个平面的两条直线平行;故选D.答案:D2.解析:对于A、B、D均可能出现l∥β,而对于C是正确的.答案:C3.D4.D5.解析:用线面垂直的性质和面面平行的性质可判断①④正确,②中m,n可以平行或异面;③中n可以在α内.答案:C6.①②7.①②③④8.解析:此题的破解可采用二个极端位置法,即对于F位于DC的中点时,t=1,随着F点到C点时,因CB⊥AB,CB⊥DK,∴CB⊥平面ADB,即有CB⊥BD,对于CD=2,BC=1,∴BD=,又AD=1,AB=2,因此有AD⊥BD,则有t=,因此t的取值范围是.答案:9.解析:(1)证明:因为四棱锥P-ABCD的底面是边长为1的正方形,PA=1,PD=,所以PD2=PA2+AD2,所以PA⊥AD.又PA⊥CD,AD∩CD=D,所以PA⊥平面ABCD.(2)四棱锥P-ABCD的底面积为1,因为PA⊥平面ABCD,所以四棱锥P-ABCD的高为1,所以四棱锥P-ABCD的体积为.10.解析:(1)取AB的中点E,连结DE,CE,因为ADB是等边三角形,所以DE⊥AB.当平面ADB⊥平面ABC时,因为平面ADB∩平面ABC=AB,所以DE⊥平面ABC,可知DE⊥CE,由已知可得DE=,EC=1,在Rt△DEC中,CD==2.(2)当△ADB以AB为轴转动时,总有AB⊥CD.证明:①当D在平面ABC内时,因为AC=BC,AD=BD,所以C,D都在线段AB的垂直平分线上,即AB⊥CD.②当D不在平面ABC内时,由(1)知AB⊥DE.又因AC=BC,所以AB⊥CE.又DE,CE为相交直线,所以AB⊥平面CDE,由CD⊂平面CDE,得AB⊥CD.综上所述,总有AB⊥CD.




 一年级数学上册期中试卷(word版)
一年级数学上册期中试卷(word版) (北京卷)高考数学理科试题word版
(北京卷)高考数学理科试题word版 北京市西城区2011年高三一模试卷数学(理科)+参考答案
北京市西城区2011年高三一模试卷数学(理科)+参考答案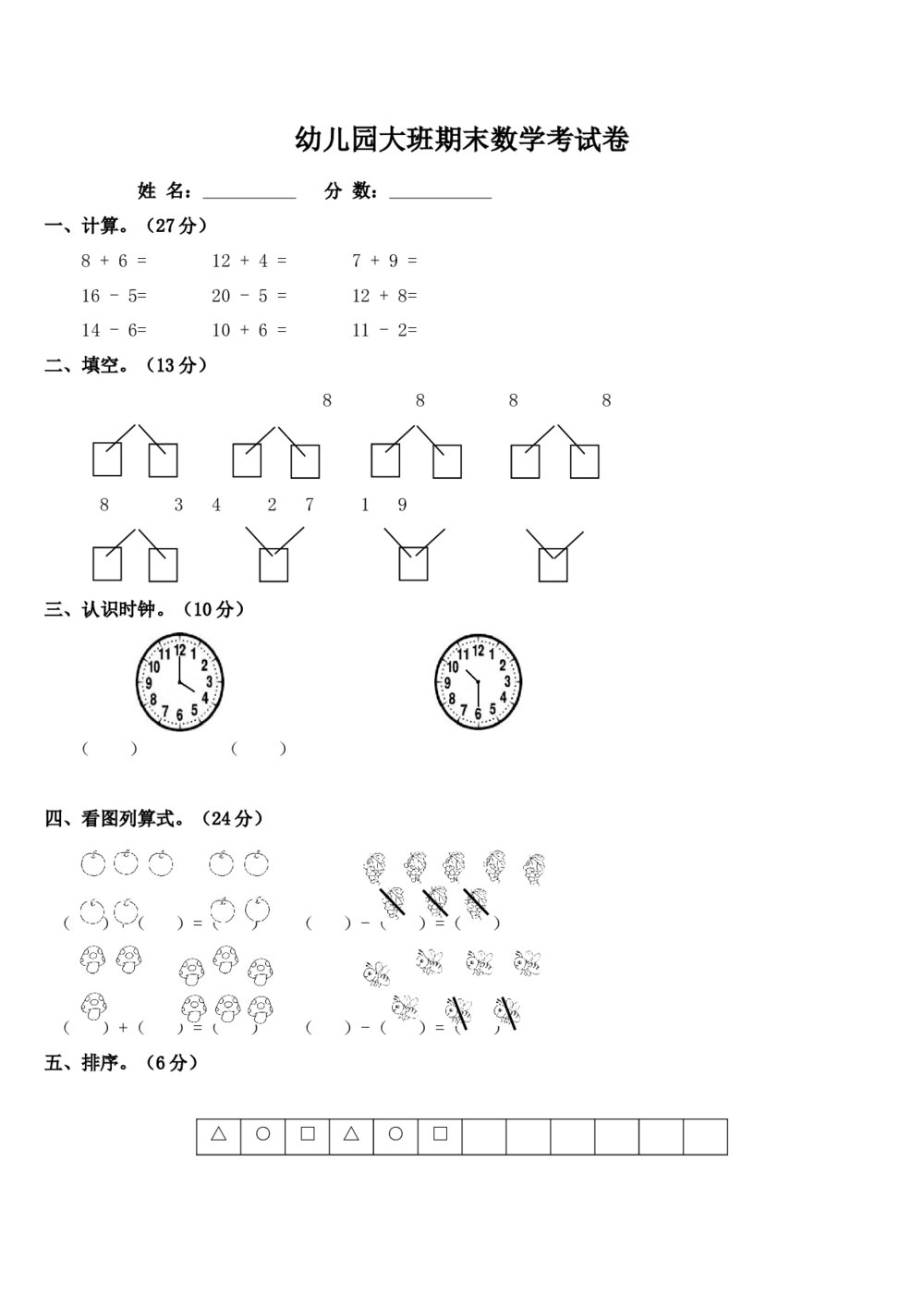 幼儿园大班期末数学考试卷(word版)
幼儿园大班期末数学考试卷(word版) 六年级下册数学期末考试试卷+参考答案
六年级下册数学期末考试试卷+参考答案 2021年全国统一高考数学试卷(文科)(新课标ⅰ)
2021年全国统一高考数学试卷(文科)(新课标ⅰ)