









试读已结束,还剩2页未读,您可下载完整版后进行离线阅读
《北京市西城区2011年高三一模试卷数学(理科)+参考答案》是由用户上传到老师板报网,本为文库资料,大小为466.5 KB,总共有12页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 12页
- 466.5 KB
- VIP模板
- doc
- 数字产品不支持退货
开始是否i输出结束2iSS1ii①1,1Si北京市西城区2011年高三一模试卷数学(理科)2011.4一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{5}AxxZ,{20}Bxx,则AB等于(A)(2,5)(B)[2,5)(C){2,3,4}(D){3,4,5}2.下列给出的函数中,既不是奇函数也不是偶函数的是(A)2xy(B)2yxx(C)2yx(D)3yx3.设3log2a,3log4b,5.0c,则(A)abc(B)bca(C)cab(D)bac4.设向量(1,sin)a,(3sin,1)b,且//ab,则cos2等于(A)3(B)3(C)3(D)35.阅读右侧程序框图,为使输出的数据为31,则①处应填的数字为(A)4(B)5(C)6(D)76.已知函数①xxycossin,②xxycossin22,则下列结论正确的是(A)两个函数的图象均关于点(,0)4成中心对称(B)两个函数的图象均关于直线4x成中心对称(C)两个函数在区间(,)44上都是单调递增函数(D)两个函数的最小正周期相同7.已知曲线1:(0)Cyxx及两点11(,0)Ax和22(,0)Ax,其中210xx.过1A,2A分别作x轴的垂线,交曲线C于1B,2B两点,直线12BB与x轴交于点33(,0)Ax,那么(A)312,,2xxx成等差数列(B)312,,2xxx成等比数列(C)132,,xxx成等差数列(D)132,,xxx成等比数列8.如图,四面体OABC的三条棱OCOBOA,,两两垂直,2OBOA,3OC,D为四面体OABC外一点.给出下列命题.①不存在点D,使四面体ABCD有三个面是直角三角形②不存在点D,使四面体ABCD是正三棱锥③存在点D,使CD与AB垂直并且相等④存在无数个点D,使点O在四面体ABCD的外接球面上其中真命题的序号是(A)①②(B)②③(C)③(D)③④二、填空题:本大题共6小题,每小题5分,共30分.9.在复平面内,复数2i1i对应的点到原点的距离为_____.10.如图,从圆O外一点P引圆O的切线PA和割线PBC,已知22PA,4PC,圆心O到BC的距离为3,则圆O的半径为_____.11.已知椭圆:Ccos,()2sinxyR经过点1(,)2m,则m______,离心率e______.12.一个棱锥的三视图如图所示,则这个棱锥的体积为_____.13.某展室有9个展台,现有3件展品需要展出,要求每件展品独自占用1个展台,并且3件展品所选用的展台既不在两端又不相邻,则不同的展出方法有______种;如果进一步要求3件展品所选用的展台之间间隔不超过两个展位,则不同的展出方法有____种.14.已知数列{}na的各项均为正整数,对于,3,2,1n,有1135,2nnnnnnkkaaaaaa为奇数为偶数.其中为使为奇数的正整数,,当111a时,100a______;若存在*mN,当nm且na为奇数时,na恒为常数p,则p的值为______.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)PABCO•OABDC正(主)视图俯视图侧(左)视图344333设ABC中的内角A,B,C所对的边长分别为a,b,c,且54cosB,2b.(Ⅰ)当35a时,求角A的度数;(Ⅱ)求ABC面积的最大值.16.(本小题满分13分)甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为11,,23p.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14.(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;(Ⅱ)求p的值;(Ⅲ)设甲、乙、丙三人中破译出密码的人数为X,求X的分布列和数学期望EX.17.(本小题满分13分)如图,ABCD是边长为3的正方形,DE平面ABCD,DEAF//,AFDE3,BE与平面ABCD所成角为060.(Ⅰ)求证:AC平面BDE;(Ⅱ)求二面角DBEF的余弦值;(Ⅲ)设点M是线段BD上一个动点,试确定点M的位置,使得//AM平面BEF,并证明你的结论.18.(本小题满分14分)已知函数2(1)()axfxx,其中0a.(Ⅰ)求函数()fx的单调区间;(Ⅱ)若直线10xy是曲线()yfx的切线,求实数a的值;(Ⅲ)设2()ln()gxxxxfx,求()gx在区间[1,e]上的最大值.(其中e为自然对数的底数)ABCDFE19.(本小题满分14分)已知抛物线22(0)ypxp的焦点为F,过F的直线交y轴正半轴于点P,交抛物线于,AB两点,其中点A在第一象限.(Ⅰ)求证:以线段FA为直径的圆与y轴相切;(Ⅱ)若1FAAP,2BFFA,1211[,]42,求2的取值范围.20.(本小题满分13分)定义),,,(21naaa12231||||||nnaaaaaa为有限项数列{}na的波动强度.(Ⅰ)当(1)nna时,求12100(,,,)aaa;(Ⅱ)若数列,,,abcd满足()()0abbc,求证:(,,,)(,,,)abcdacbd;(Ⅲ)设{}na各项均不相等,且交换数列{}na中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列{}na一定是递增数列或递减数列.北京市西城区2011年高三一模试卷参考答案及评分标准数学(理科)2011.4一、选择题:本大题共8小题,每小题5分,共40分.题号12345678答案CBADBCAD二、填空题:本大题共6小题,每小题5分,共30分.9.210.211.415,3212.1213.60,4814.62;1或5注:11题,13题,14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分)解:(Ⅰ)因为54cosB,所以53sinB.……………………2分因为35a,2b,由正弦定理BbAasinsin可得21sinA.…………………4分因为ba,所以A是锐角,所以o30A.……………………6分(Ⅱ)因为ABC的面积acBacS103sin21,……………………7分所以当ac最大时,ABC的面积最大.因为Baccabcos2222,所以acca58422.……………………9分因为222acac,所以8245acac,……………………11分所以10ac,(当10ac时等号成立)……………………12分所以ABC面积的最大值为3.……………………13分16.(本小题满分13分)解:记“甲、乙、丙三人各自破译出密码”分别为事件321,,AAA,依题意有12311(),(),(),23PAPAPAp且321,,AAA相互独立.(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为121()PAA1221233.…………………3分(Ⅱ)设“三人中只有甲破译出密码”为事件B,则有()PB123()PAAA=121(1)233pp,…………………5分所以1134p,14p.……………………7分(Ⅲ)X的所有可能取值为3,2,1,0.……………………8分所以1(0)4PX,(1)PXP123()AAAP123()AAAP123()AAA111312111423423424,(2)PXP123()AAAP123()AAAP123()AAA11312111112342342344,(3)PX=P123()AAA=111123424.……………………11分X分布列为:X0123P14112414124……………………12分所以,1111113()012342442412EX.……………………13分17.(本小题满分13分)(Ⅰ)证明:因为DE平面ABCD,所以ACDE.……………………2分因为ABCD是正方形,所以BDAC,从而AC平面BDE.……………………4分(Ⅱ)解:因为DEDCDA,,两两垂直,所以建立空间直角坐标系xyzD如图所示.因为BE与平面ABCD所成角为060,即60DBE,………………5分所以3DBED.由3AD可知36DE,6AF.………………6分则(3,0,0)A,(3,0,6)F,(0,0,36)E,(3,3,0)B,(0,3,0)C,所以(0,3,6)BF,(3,0,26)EF,………………7分设平面BEF的法向量为n(,,)xyz,则00BFEFnn,即3603260yzxz,令6z,则n(4,2,6).…………………8分因为AC平面BDE,所以CA为平面BDE的法向量,(3,3,0)CA,所以613cos,133226CACACAnnn.…………………9分因为二面角为锐角,所以二面角DBEF的余弦值为1313.………………yBCAEzDFxyBCAEzDFxM10分(Ⅲ)解:点M是线段BD上一个动点,设(,,0)Mtt.则(3,,0)AMtt,因为//AM平面BEF,所以AMn0,…………………11分即4(3)20tt,解得2t.…………………12分此时,点M坐标为(2,2,0),13BMBD,符合题意.…………………13分18.(本小题满分14分)解:(Ⅰ)3(2)()axfxx,(0x),……………3分在区间(,0)和(2,)上,()0fx;在区间(0,2)上,()0fx.所以,()fx的单调递减区间是(,0)和(2,),单调递增区间是(0,2).………4分(Ⅱ)设切点坐标为00(,)xy,则002000030(1)10(2)1axyxxyaxx……………7分(1个方程1分)解得01x,1a.……………8分(Ⅲ)()gxln(1)xxax,则()ln1gxxa,…………………9分解()0gx,得1eax,所以,在区间1(0,e)a上,()gx为递减函数,在区间1(e,)a上,()gx为递增函数.……………10分当1e1a,即01a时,在区间[1,e]上,()gx为递增函数,所以()gx最大值为(e)eegaa.………………11分当1eea,即2a时,在区间[1,e]上,()gx为递减函数,所以()gx最大值为(1)0g.………………12分当11










 (安徽卷)高考理科数学(解析版)
(安徽卷)高考理科数学(解析版)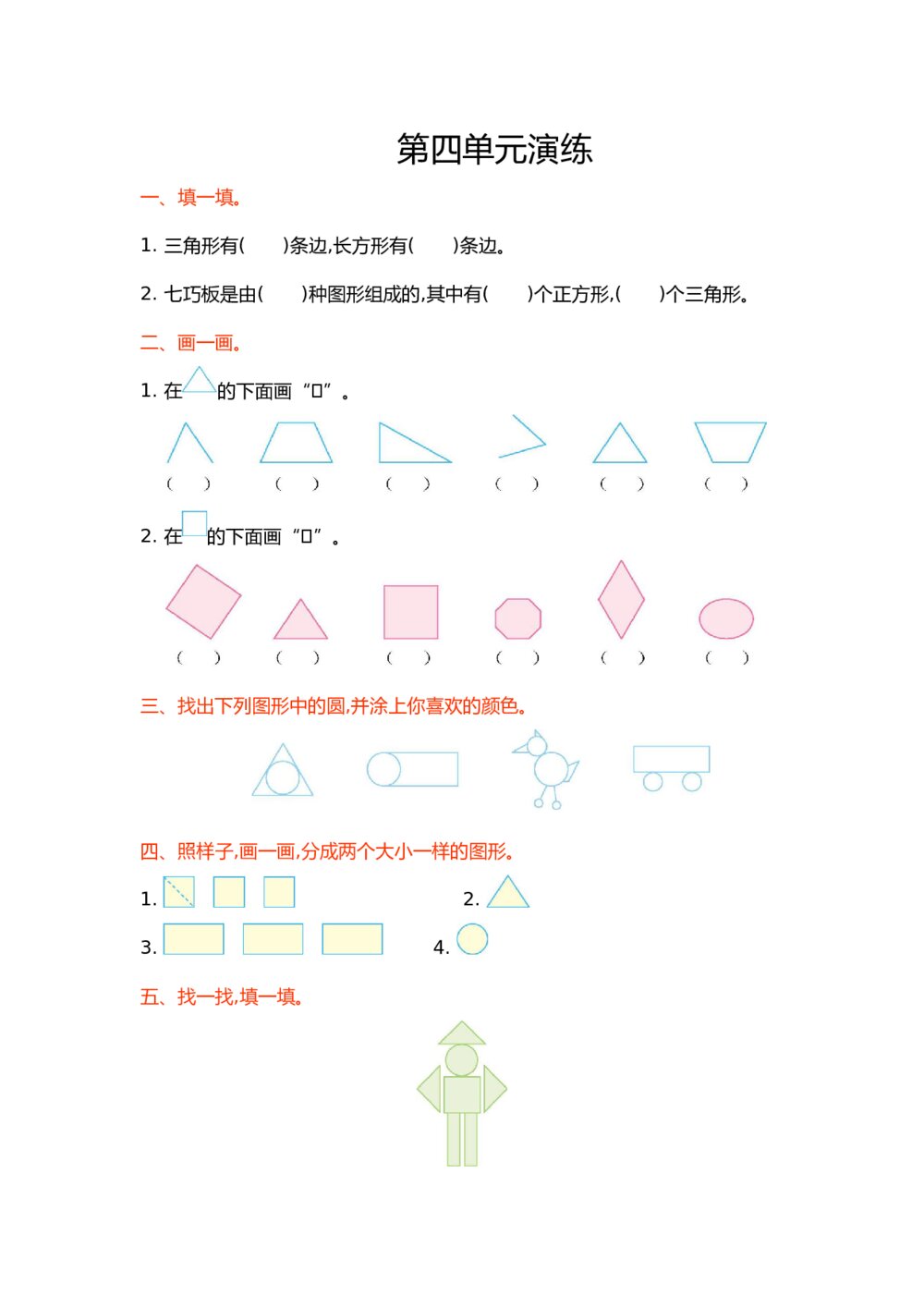 新北师大版小学一年级下册数学第四单元优秀检测试卷有答案
新北师大版小学一年级下册数学第四单元优秀检测试卷有答案 2020年全国统一高考数学(文科)试卷(新课标Ⅲ)+(答案解析版)
2020年全国统一高考数学(文科)试卷(新课标Ⅲ)+(答案解析版) 2011年高考一轮课时训练(理)4.3定积分的概念,微积分基本定理及简单应用+答案解析 (通用版).DOC
2011年高考一轮课时训练(理)4.3定积分的概念,微积分基本定理及简单应用+答案解析 (通用版).DOC 2011北京东城区高三二模数学试题试卷+答案(理科)
2011北京东城区高三二模数学试题试卷+答案(理科)![六年级数学奥数《第四讲[1]几何-平面部分》教师版](https://img.banbaow.com/uploadfile/2023/0531/0d3efc87daa1f139531e7/0.jpg) 六年级数学奥数《第四讲[1]几何-平面部分》教师版
六年级数学奥数《第四讲[1]几何-平面部分》教师版