


《2011年高考一轮课时训练(理)4.1导数的概念及其运算+参考答案(通用版)》是由用户上传到老师板报网,本为文库资料,大小为121 KB,总共有3页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 3页
- 121 KB
- VIP模板
- doc
- 数字产品不支持退货
第四章 导数及其应用第一节 导数的概念及其运算题号12345答案一、选择题1.如果质点A按规律s=2t3运动,则在t=3s时的瞬时加速度为( )A.18 B.24 C.36 D.542.(2008年辽宁卷)设P为曲线C:y=x2+2x+3上的点,且曲线C在点P处切线倾斜角的取值范围为,则点P横坐标的取值范围为( )A.B.C.D.3.设f0(x)=sinx,f1(x)=f′0(x),f2(x)=f′1(x),…,fn+1(x)=f′n(x)(n∈N),则f2009(x)=( )A.sinxB.-sinxC.cosxD.-cosx4.(2009年江门模拟)曲线y=ex在点(2,e2)处的切线与坐标轴所围三角形的面积为( )A.e2B.2e2C.e2D.5.(2009年江西卷)若存在过点(1,0)的直线与曲线y=x3和y=ax2+x-9都相切,则a等于( )A.-1或-B.-1或C.-或-D.-或7二、填空题6.(2009年桂林模拟)半径为r的圆的面积S(r)=πr2,周长C(r)=2πr,若将r看作(0,+∞)上的变量,则(πr2)′=2πr①,①式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于①的式子:_______________________②,②式可以用语言叙为:________________________.7.已知f(x)=x2+2x·f′(1),则f′(0)=________.8.(2009年福建卷)若曲线f(x)=ax3+lnx存在垂直于y轴的切线,则实数a取值范围是________.三、解答题9.如右图所示,已知A为抛物线C:y=2x2上的点,直线l1过点A,且与抛物线C相切,直线l2:x=a交抛物线C于点B,交直线l1于点D.(1)求直线l1的方程;(2)求△ABD的面积S1.10.(2008年天津卷)已知函数f=x++b,其中a,b∈R.(1)若曲线y=f在点P处的切线方程为y=3x+1,求函数f的解析式;(2)讨论函数f的单调性;(3)若对于任意的a∈,不等式f≤10在上恒成立,求b的取值范围.参考答案1.C2.解析:本小题主要考查利用导数的几何意义求切线斜率问题.依题设切点P的横坐标为x0,且y′=2x0+2=tanα(α为点P处切线的倾斜角),又∵α∈,∴0≤2x0+2≤1,∴x0∈.答案:A3.C4.解析:y′=(ex)′=ex,曲线在点(2,e2)处的切线斜率为e2,因此切线方程为y-e2=e2(x-2),则切线与坐标轴交点为A(1,0),B(0,-e2),所以:S△AOB=×1×e2=.答案:D5.解析:设过(1,0)的直线与y=x3相切于点(x0,x),所以切线方程为y-x=3x(x-x0)即y=3xx-2x,又(1,0)在切线上,则x0=0或x0=,当x0=0时,由y=0与y=ax2+x-9相切可得a=-,当x0=时,由y=x-与y=ax2+x-9相切可得a=-1.答案:A6.解析:V球=πR3,又(πR3)′=4πR2,故②式可填(πR3)′=4πR2,用语言叙述为“球的体积函数的导数等于球的表面积函数.”答案:(πR3)′=4πR2 球的体积函数的导数等于球的表面积函数7.-48.解析:由题意可知f′(x)=2ax2+,又因为存在垂直于y轴的切线,所以2ax2+=0⇒a=-(x>0)⇒a∈(-∞,0).答案:(-∞,0)9.解析:(1)由条件知点A为直线l1与抛物线C的切点,∵y′=4x,∴直线l1的斜率k=-4,即直线l1的方程为y-2=-4(x+1), 即4x+y+2=0.(2)点A的坐标为(-1,2),由条件可求得点B的坐标为(a,2a2),点D的坐标为(a,-4a-2),∴△ABD的面积S1为S1=×|2a2-(-4a-2)|×|-1-a|=|(a+1)3|=-(a+1)3.10.解析:(1)f′(x)=1-,由导数的几何意义得f′(2)=3,于是a=-8.由切点P(2,f(2))在直线y=3x+1上可得-2+b=7,解得b=9.所以函数f(x)的解析式为f(x)=x-+9.(2)f′(x)=1-.当a≤0时,显然f′(x)>0(x≠0).这时f(x)在(-∞,0),(0,+∞)上是增函数.当a>0时,令f′(x)=0,解得x=±.当x变化时,f′(x),f(x)的变化情况如下表:x(-∞,-)-(-,0)(0,)(,+∞)f′(x)+0--0+f(x)↗极大值↘↘极小值↗所以f(x)在(-∞,-),(,+∞)内是增函数,在(-,0),(0,)内是减函数.(3)由(2)知,f(x)在上的最大值为f与f(1)的较大者,对于任意的a∈,不等式f(x)≤10在上恒成立,当且仅当,即,对任意的a∈成立.从而得b≤,所以满足条件的b的取值范围是.展开内容



 2012山东卷高考数学(理科)试卷
2012山东卷高考数学(理科)试卷 最新6年高考4年模拟试题试卷--第六章第二节数列的应用(答案解析)
最新6年高考4年模拟试题试卷--第六章第二节数列的应用(答案解析)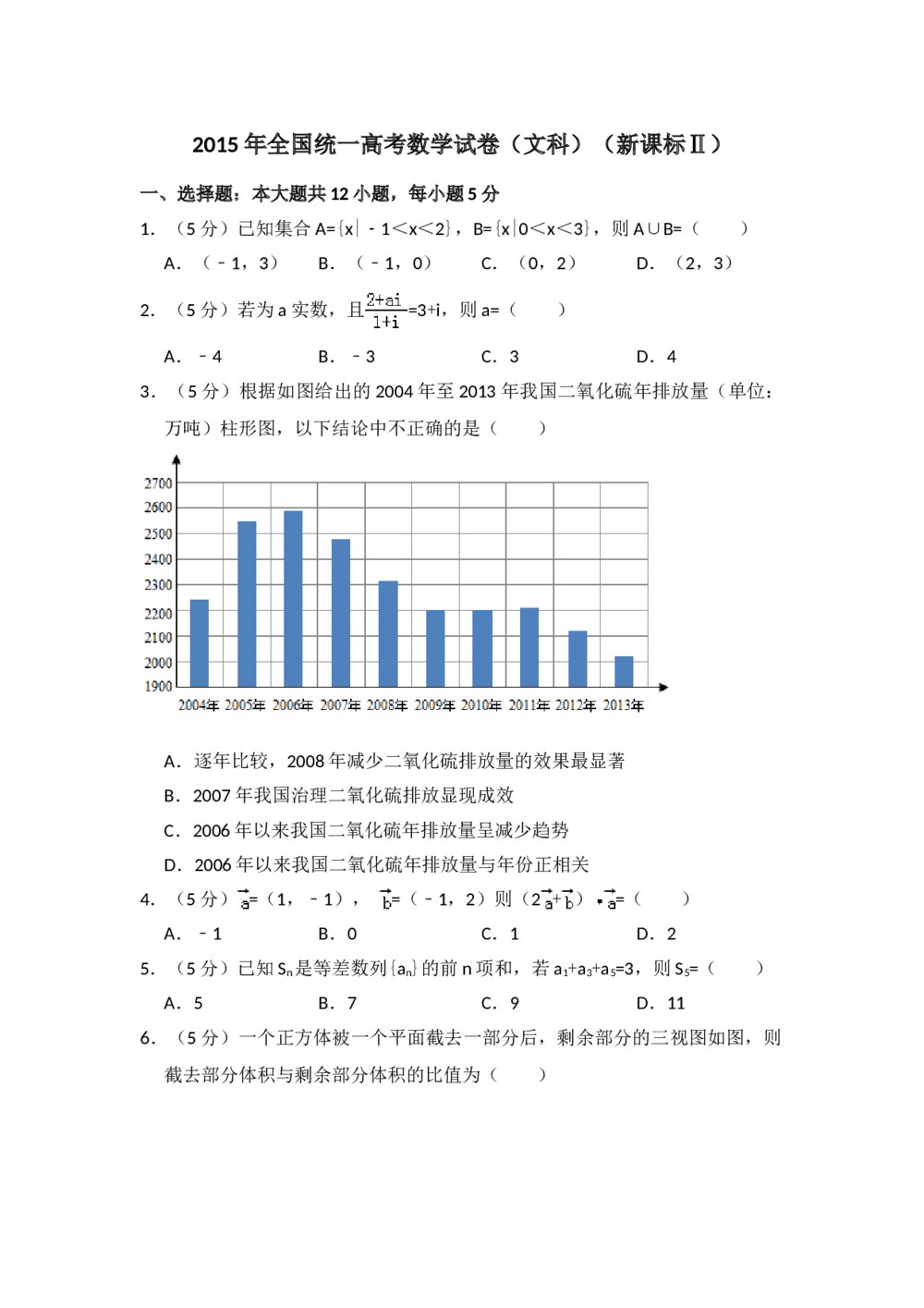 2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析
2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析 2020年全国统一高考数学(文科)试卷新课标Ⅱ)(原卷版)
2020年全国统一高考数学(文科)试卷新课标Ⅱ)(原卷版) 2016年高考(文科)数学试卷(新课标Ⅱ)+(答案)
2016年高考(文科)数学试卷(新课标Ⅱ)+(答案) 高中数学《几何概型》word学案
高中数学《几何概型》word学案