



《2011年高考一轮课时训练(理)2.3数学归纳法+答案解析(通用版).DOC》是由用户上传到老师板报网,本为文库资料,大小为121.5 KB,总共有4页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 4页
- 121.5 KB
- VIP模板
- doc
- 数字产品不支持退货
第三节数学归纳法一、选择题1.用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”,从“k到k+1”左端需增乘的代数式为( )A.2k+1 B.2(2k+1)C.D.解析:当n=1时,式子显然成立.当n=k(k∈N*,且k≥1)时,左边=(k+1)(k+2)·…·(k+k),当n=k+1时,左边=(k+1+1)(k+1+2)·…·(k+1+k)(k+1+k+1)=(k+2)(k+3)·…·(k+k)(k+1+k)(k+1+k+1)=(k+1)(k+2)·…·(k+k)=(k+1)(k+2)·…·(k+k)2(2k+1).答案:B2.记凸k边形的内角和为f(k),则f(k+1)-f(k)=( )A.B.πC.πD.2π答案:B3.如果命题P(n)对n=k成立,则它对n=k+1也成立,现已知P(n)对n=4不成立,则下列结论正确的是( )A.P(n)对n∈N*成立B.P(n)对n>4且n∈N*成立C.P(n)对n<4且n∈N*成立D.P(n)对n≤4且n∈N*不成立解析:由题意可知,P(n)对n=3不成立(否则n=4也成立),同理可推得P(n)对n=2,n=1也不成立.答案:D4.用数学归纳法证明“1+++…+<n(n∈N*,)”时,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项数是( )A.2k-1B.2k-1C.2kD.2k+1解析:左边的特点:分母逐渐增加1,末项为;由n=k,末项为,而n=k+1,末项为=,故应增加的项数为2k.答案:C5.若把正整数按下图所示的规律排序,则从2002到2004的箭头方向依次为( )答案:D二、填空题6.用数学归纳法证明-1+3-5+…+n=nn,当n=1时,左边应为________.答案:-17.已知a1=,an+1=,则a2,a3,a4,a5的值分别为________,由此猜想an=________.解析:a2====,同理a3===,a4==,a5==,猜想an=.答案:、、、 8.(2009年广东执信中学月考)观察下列式子:1+<,1++<,1+++<,…,则可归纳出____________________.解析:1+<,即1+<,1++<,即1++<,归纳为:1+++…+<(n∈N+).答案:1+++…+<(n∈N+)三、解答题9.已知y=f(x)满足f(n-1)=f(n)-lgan-1(n≥2,n∈N)且f(1)=-lga,是否存在实数α,β,使f(n)=(αn2+βn-1)·lga对任何n∈N*都成立,证明你的结论.解析:∵f(n)=f(n-1)+lgan-1,令n=2,则f(2)=f(1)+lga=-lga+lga=0.又f(1)=-lga,∴,∴.∴f(n)=lga.现证明如下:(1)当n=1时,显然成立.(2)假设n=k(k∈N*,且k≥1)时成立,即f(k)=lga,则n=k+1时,f(k+1)=f(k)+lgak=f(k)+klga=lga=lga.则当n=k+1时,等式成立.综合(1)(2)可知,存在实数α、β且α=,β=-,使f(n)=(αn2+βn-1)lga对任意n∈N+都成立.10.(2009年南昌月考)设曲线y=+bx2+cx在点处的切线斜率为k(x),且k(-1)=0.对一切实数x,不等式x≤k(x)≤(x2+1)恒成立(a≠0).(1)求k(1)的值;(2)求函数k(x)的表达式;(3)求证:++…+>.解析:(1)由x≤k(x)≤(x2+1)得1≤k(1)≤1,所以k(1)=1.(2)k(x)=y′=ax2+bx+c(a≠0),由k(1)=1,k(-1)=0得⇒a+c=,b=.又x≤k(x)≤(x2+1)恒成立,则由ax2-x+c≥0(a≠0)恒成立得⇒a=c=,同理由(-a)x2+x+-c≥0恒成立,也可得:a=c=.综上a=c=,b=,所以k(x)=x2+x+.(3)证明:法一(分析法):k(n)==⇒=.要证原不等式成立,即证++…+>.因为>=-,所以++…+>-+-+…+-=-=,所以++…+>.法二:(数学归纳法)由k(n)==⇒=.①当n=1时,左边=1,右边=,左边>右边,所以n=1,不等式成立.②假设当n=m(m∈N*,且m≥1)时,不等式成立,即++…>.当n=m+1时,左边=++…++>+=由-=>0所以++…++>即当n=m+1时,不等式也成立.综上得++…+>.展开内容




 2010年高考数学试题分类汇编--不等式+(答案解析)
2010年高考数学试题分类汇编--不等式+(答案解析) 2002年上海高考数学(理科)试卷(word版)+参考答案
2002年上海高考数学(理科)试卷(word版)+参考答案 2011年四川高考数学(理科)试卷答案解析版
2011年四川高考数学(理科)试卷答案解析版 高考文科数学二轮专题复习题:《专题4 第1讲 三视图及空间几何体的计算问题》
高考文科数学二轮专题复习题:《专题4 第1讲 三视图及空间几何体的计算问题》 2015年3月德阳市四校高三联考数学(文科)试题+参考答案
2015年3月德阳市四校高三联考数学(文科)试题+参考答案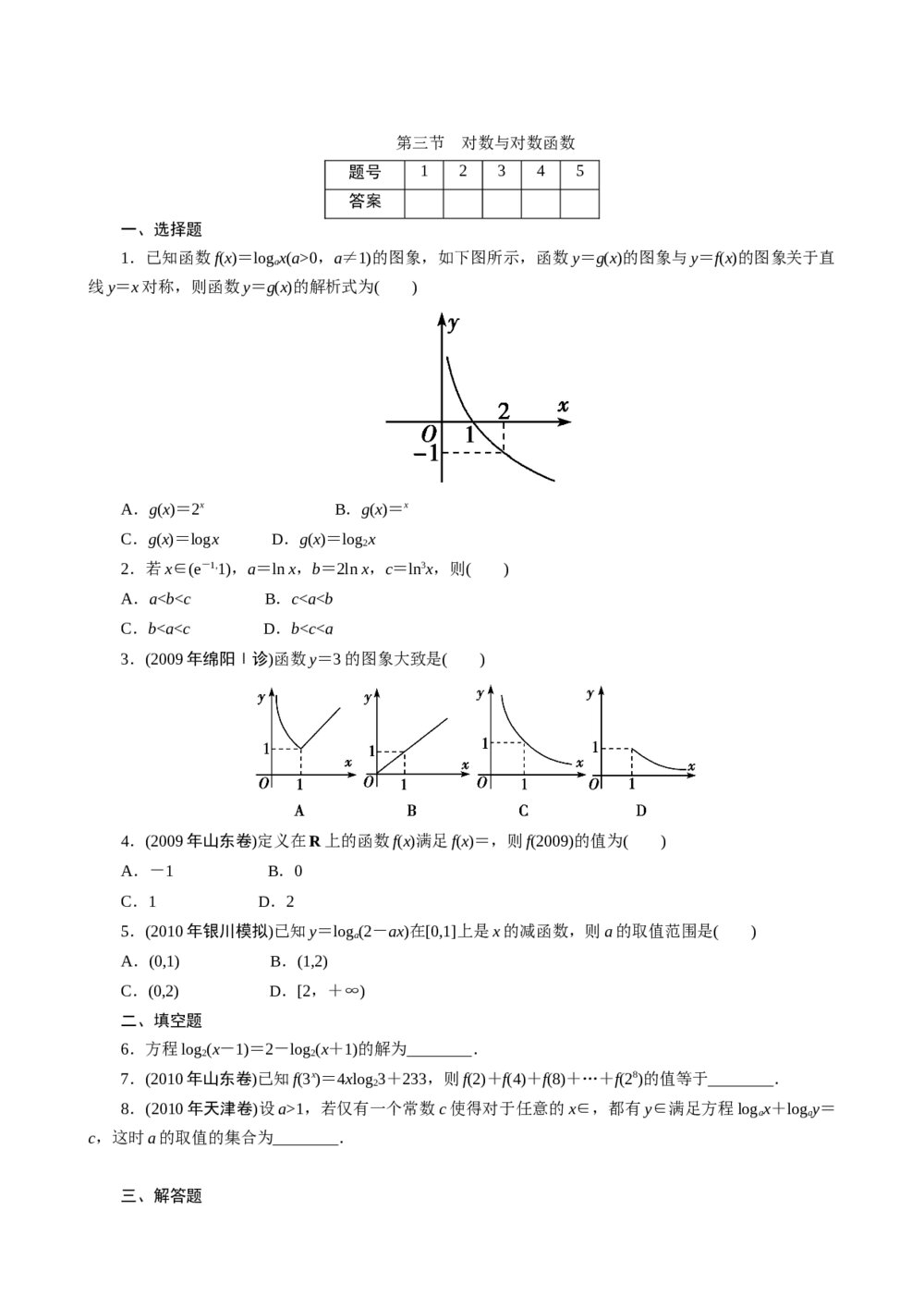 2011年高考一轮课时训练(理)3.2.3对数与对数函数+参考答案(通用版)
2011年高考一轮课时训练(理)3.2.3对数与对数函数+参考答案(通用版)