









试读已结束,还剩2页未读,您可下载完整版后进行离线阅读
《2012年普通高等学校招生全国统一考试(预测卷2) 数学(理科)试卷+参考答案》是由用户上传到老师板报网,本为文库资料,大小为528.5 KB,总共有12页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 12页
- 528.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2012年普通高等学校招生全国统一考试(预测卷2)数学(理科)试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至5页,考试结束后,将本试卷和答题卡一并交回.参考公式:球的表面积公式:S=24R,其中R表示球的半径第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题意要求的.1.已知全集},2|{},2|{,NnnxxBNnxxARUn与集合,则正确表示集合BA、关系的韦恩(Venn)图是2.在复平面内,复数21i对应的点到直线1yx的距离是A.22B.2C.2D.223.下列有关选项正确的是A.若qp为真命题,则pq为真命题.B.“5x”是“2450xx”的充分不必要条件.C.命题“若1x,则2230xx”的否命题为:“若1x,则2320xx”.D.已知命题p:Rx,使得210xx,则p:Rx,使得210xx.4.若}{na为等差数列,nS是其前n项和,且32211S,则6tana的值为A.3B.3C.3D.335.一个正三棱柱的主(正)视图是长为3,宽为2的矩形,则它的外接球的表面积等于A.16B.12C.8D.46.已知实数,xy满足153xy,则2zxy的最小值是A.10B.3C.3D.107.设2921101211(1)(21)(2)(2)(2)xxaaxaxax,32则01211aaaa的值为A.2B.C.2D.18.从5种不同的水果和4种不同的糖果中各选出3种,放入如图所示的6个不同区域(用数字表示)中拼盘,每个区域只放一种,且水果不能放在有公共边的相邻区域内,则不同的放法有A.2880种 B.2160种C.1440种 D.720种9.某程序流程框图如图所示,现执行该程序,输入下列函数,xxfxxf32cos)(,32sin)(,,34tan)(xxf则可以输出的函数是)(xf=A.xxf32sin)(B.xxf32cos)(C.xxf34tan)(D.非上述函数10.在空间中,下列四个命题①若三条直线两两相交,则这三条直线确定一个平面②若直线m与平面内的一条直线平行,则//m③若平面,且l,则过内一点P与垂直的直线垂直于平面④若直线a与直线b平行,且直线al,则bl其中正确命题的个数是A.3B.2C.1D.011.过抛物线xy42的焦点F作相互垂直的两条弦AB和CD,则||||CDAB的最小值是A.58B.16C.8D.712.设函数fx在R上的导函数为\'fx,且22\'fxxfxx,下面的不等式在R上恒成立的是A.0fxB.0fxC.fxxD.fxx第Ⅱ卷二、填空题:本大题共4小题,每小题5分,满分20分.13.已知函数为无理数,为有理数,x0x1)(xf,则关于x的不等式0)1()()]1()([2xfxfxxfxfx的解集为_______________.14.在ABC中,,120,ABCABBC则以BA,为焦点且过点C的双曲线的离心率为.13.某大学艺术系表演专业的报考人数连创新高,报名刚结束,某考生想知道这次报考该专业的人数。已知该专业考生的考号是从0001,0002,…这样从小到大顺序依次排列的,他随机了解了50个考生的考号,经计算,这50个考号的和是25025,估计2010年报考这所大学艺术表演专业的考生大约为人.12345616.现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为24a.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .三、解答题(解答应写出文字说明,证明过程或演算步骤).17.(本小题满分12分)已知函数)3sin()6sin(2)(xωxωxf(其中为正常数,Rx)的最小正周期为.(I)求的值;(II)在△ABC中,若BA,且21)()(BfAf,求ABBC.18.(本小题满分12分)今天你低碳了吗?近来,国内网站流行一种名为“碳排放计算器”的软件,人们可以由此计算出自己每天的碳排放量。例如:家居用电的碳排放量(千克)=耗电度数0.785,汽车的碳排放量(千克)=油耗公升数0.785等。东北育才中学高一某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如下:(I)如果甲、乙来自A小区,丙、丁来自B小区,求这4人中恰有2人是低碳族的概率;(II)A小区经过大力宣传,每周非低碳族中有20%的人加入到低碳族的行列.如果2周后随机地从A小区中任选25人,记表示25个人中低碳族人数,求E.19.(本小题满分12分)如图,已知点P在正方体ABCDABCD的对角线BD上,60PDA.(Ⅰ)求DP与CC所成角的大小;ABCDPABCD(Ⅱ)求DP与平面AADD所成角的大小.20.(本小题满分12分)已知函数aaxxxxfln)1(21)(2.(Ⅰ)若23a,求函数)(xf的极值;(Ⅱ)若对任意的)3,1(x,都有0)(xf成立,求a的取值范围.21.(本小题满分12分)已知两点(2,3)M,(2,3)N在椭圆)0(1:2222babyaxC上,斜率为12的直线与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为123.w(I)求椭圆C的方程;(II)若点N到直线AM,BM距离的和为62,试判断MAB的形状.请考生在(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.22.(本小题满分10分)选修4-1:几何证明选讲如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.(I)求AC的长;(II)求证:BE=EF.23.(本小题满分10分)选修4-4:坐标系与参数方程已知直线的参数方程是)(242222是参数ttytx,圆C的极坐标方程为)4cos(2.(I)求圆心C的直角坐标;(II)由直线上的点向圆C引切线,求切线长的最小值.24.(本小题10分)选修4-5:不等式选讲已知关于x的不等式:12mx的整数解有且仅有一个值为2.(Ⅰ)求整数m的值;(Ⅱ)在(I)的条件下,解不等式:mxx31.参考答案二、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题意要求的.1.A2.D3.B4.B5.C6.D7.C8.A9.B10.C11.B12.A二、填空题:本大题共4小题,每小题5分,共20分.13.}1{14.21315.100016.83a三、解答题(解答应写出文字说明,证明过程或演算步骤)17.解:(1)∵2)3(cos)6sin(2)3sin()6sin(2)(xωxωxωxωxf)6cos()6sin(2xωxω)32sin(xω.……………4分而)(xf的最小正周期为,为正常数,∴ω22,解之,得1.………………………6分(2)由(1)得)32sin()(xxf.若x是三角形的内角,则x0,∴35323x.令21)(xf,得21)32sin(x,∴632x或6532x,解之,得4x或127x.………………………8分由已知,BA,是△ABC的内角,BA且21)()(BfAf,∴4A,127B∴6BAC.……………10分又由正弦定理,得221226sin4sinsinsinCAABBC.………12分18.解:(I)记这4人中恰好有2人是低碳族为事件A,P(A)=100335454212151542121451512121……………4分(II)设A小区有a人,2周后非低碳族的概率258)511(221aap,……6分2周后低碳族的概率p=25172581,……………………………………8分依题意~B(25,2517),所以E=252517=17………………………………12分19解:方法一:如图,以D为原点,DA为单位长建立空间直角坐标系Dxyz.则(100)DA,,,(001)CC,,.连结BD,BD.在平面BBDD中,延长DP交BD于H.设(1)(0)DHmmm,,,由已知60DHDA,,由DHDADHDADHDA,cos||||cosDADHDADHDADH,可得2221mm.解得22m,所以22122DH,,.………4分(Ⅰ)因为220011222cos212DHCC,,所以45DHCC,.即DP与CC所成的角为45.………8分(Ⅱ)平面AADD的一个法向量是(010)DC,,.因为220110122cos212DHDC,,所以60DHDC,.可得DP与平面AADD所成的角为30.………12分方法二:如图,以D为原点,DA为单位长建立空间直角坐标系Dxyz.则(100)DA,,,(001)CC,,,)1,1,1(\'BD.设),,(zyxP则\'BDBP,),,(),1,1(zyxzyx11,则),1,1(DP,由已知,60,DADP,0242,解得22,)22,12,12(DP………4分(Ⅰ)因为22)12(222,cos\'CCDP,ABCDPABCDxyzHABCDPABCDxyzH所以45,\'CCDP.即DP与CC所成的角为45.………8分(Ⅱ)平面AADD的一个法向量是(010)DC,,.因为21)12(212,cosDCDP,所以60,DCDP.可得DP与平面AADD所成的角为30.………12分方法三:用三面角(折叠角公式)求与DPDB所成的角,再求DP长或P点坐标也可酌情给分.20.解:(I)xxxxxxf22522512,0xf,得211x,或22x,列表:x)21,0(21)2,21(2),2()(xf+0-0+)(xf极大极小函数)(xf在21x处取得极大值2ln87)21(f,函数)(xf在2x处取得极小值12ln)2(f;…………4分(II)方法1:)1(1axxxf,3,1x时,)310,2(1xx,………5分(i)当21a,即1a时,3,1x时,0xf,函数)(xf在3,1是增函数3,1x,01fxf恒成立;…………7分(ii)当3101a,即37a时,3,1x时,0xf,函数)(xf在3,1是减函数3,1x,01fxf恒成立,不合题意…………9分(iii)当31012a,即371a时,3,1x时,xf先取负,再取,最后取正,函数)(xf在3,1先递减,再递增,而01f,∴3,1x,01fxf不能恒成立;……11分综上,a的取值范围是1a.…………12分方法2:∵2121xxxx,∴aaxxxf111……6分(i)当1a时,01axf,而axxxf11不恒为0,∴函数)(xf是单调递增函数,3,1x,01fxf恒成立;………8分(ii)当1a时,令xxaxxf1)1(2,设01)1(2xax两根是)(,2121xxxx,∵2121axx,121xx,∴2110xx当x),(21xx时,0xf,xf是减函数,∴)()1()(21xffxf,而01f,∴)(0)(21xfxf…………10分若32x,∵3,1x,0xf,∴0)1()(2fxf,不可能,若32x,函数)(xf在3,1是减函数,0)1(3ff,也不可能,综上,a的取值范围是1a.…………12分方法3:41,1)1(22axxaxxf(i)当0,即13a时,函数xfy在3,1上为增函数,3,1x,01fxf恒成立;…………6分(ii)当0,即3a,或1a时,①若3a,∵3,1x,∴01)1(2xxaxxfxf在3,1增函数,3,1x,01fxf恒成立;…………8分②若1a,由0xf,得024112aax设2411,24112221aaxaax,列表:x),0(1x1x),(21xx2x),(2x)(xf+0-0+)(xf极大极小∵任意的3,1x,0xf恒成立,而01f,∴0)3(11fx,或12x,…………10分11411241122aaaaa与1a矛盾,124112aa,也与1a矛盾,以上两式都与1a矛盾,对任意的3,1x,0xf不能恒成立,综上,a的取值范围是1a.…………12分21.解:(I)设直线的方程为12yxm()mR并代入222222bxayab得:22222222()04abxmaxamab设11(,)Axy,22(,)Bxy1,21,2(,)xyR则212224maxxab,422222221abbaamxxww………2分又212121211||||||()422MANBSMNxxMNxxxx=444||21222222442abmbababaMN显然当0m时,MANBS=444||21222222442abmbababaMN=123(1)…4分由题意|MN|=6(2)222249baab(3)联立(1)、(2)、(3)解得:216a,212b即椭圆C的方程为:2211612xy(4)………6分(II)设直线MA、MB的方程分别为1(2)3ykx(5)2(2)3ykx(1,2kR)将(5)代入(4)得:222211111(1612)(9664)64192480kxkkxkk则211121641924821612kkxk211121824643kkxk………8分2211112211824612129(,)4343kkkkAkk同理:2222222222824612129(,)4343kkkkBkk2211222212122211221222121212912129434318246824624343ABkkkkyykkkkkkkxxkk………10分化简得:2212kk12kk12kk即直线MA与MB关于直线MN对称AMNBMNN到直线MA与MB距离均为32又|MN|=6AMNBMN42AMB故MAB直角三角形.…………12分22.解:(I)1,2,2PCPAPDPCPA,4PD,又2,1CEEDPC,,,CABPCACBAPACCBAPAC∽,ABACACPC,22ABPCAC,2AC…………5分(II)2ACBE,2CE,而EFBEEDCE,2212EF,BEEF.…………10分23.解:(I)sin2cos2,sin2cos22,02222yxyxC的直角坐标方程为圆,即1)22()22(22yx,)22,22(圆心直角坐标为.…………5分(II)方法1:直线上的点向圆C引切线长是6224)4(4081)242222()2222(2222ttttt,∴直线上的点向圆C引的切线长的最小值是62…………10分方法2:024yxl的普通方程为直线,圆心C到l直线距离是52|242222|,∴直线上的点向圆C引的切线长的最小值是621522…………10分24.解:(I)1|2|mx由,得2121mxm不等式的整数解为2,21221mm53m又不等式仅有一个整数解2,4m4分(II)即解不等式4|3||1|xx,.当1x时,不等式1340xxx,不等式解集为}0|{xx当13x时,不等式为134xxx,不等式解为当3x时,134xx4x,不等式解集为}4|{xx综上,不等式解为,04,10分










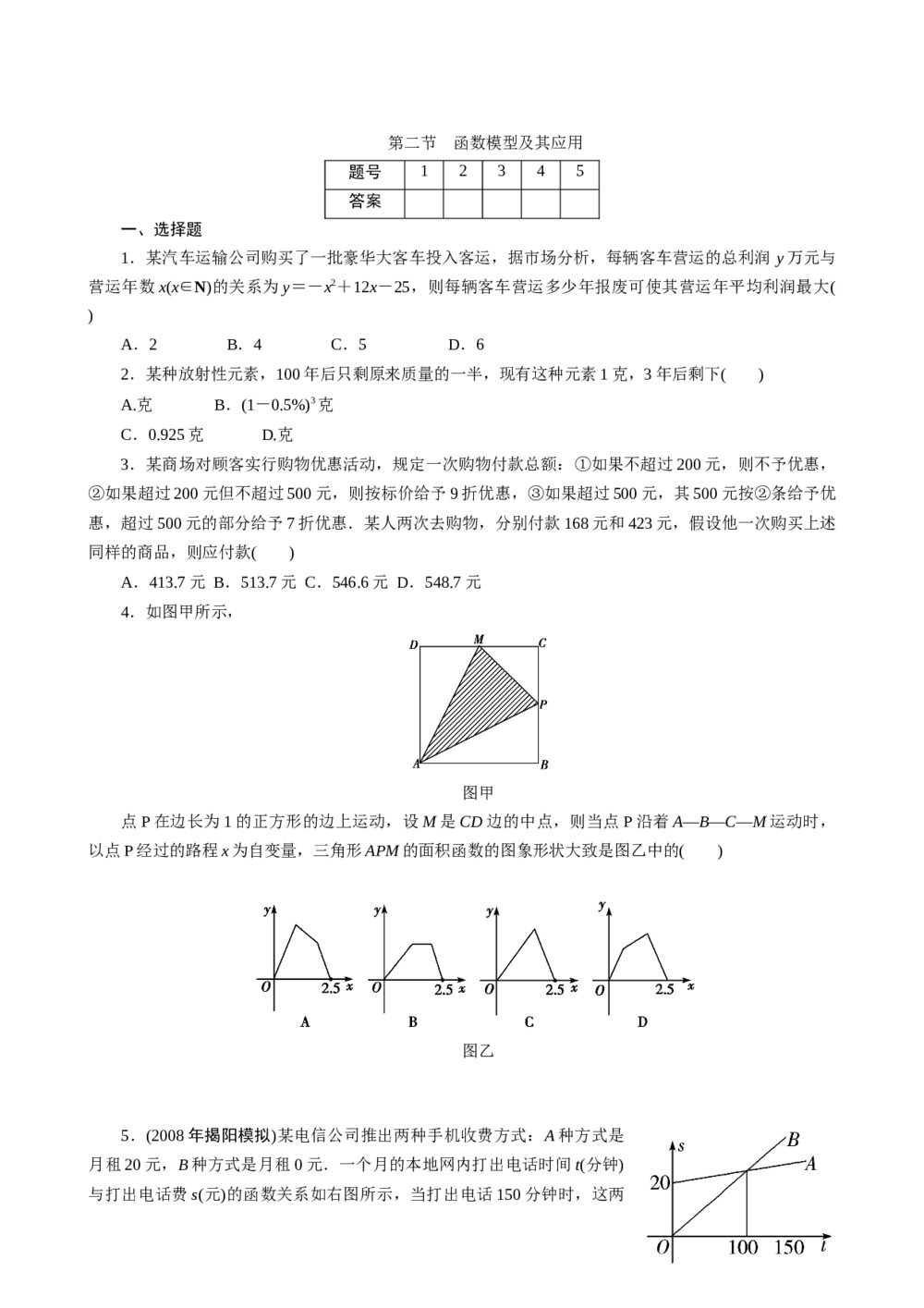 2011年高考一轮课时训练(理)3.3.2函数模型及其应用+参考答案(通用版)
2011年高考一轮课时训练(理)3.3.2函数模型及其应用+参考答案(通用版) 2021年全国统一高考数学试卷(新高考全国Ⅱ卷)
2021年全国统一高考数学试卷(新高考全国Ⅱ卷)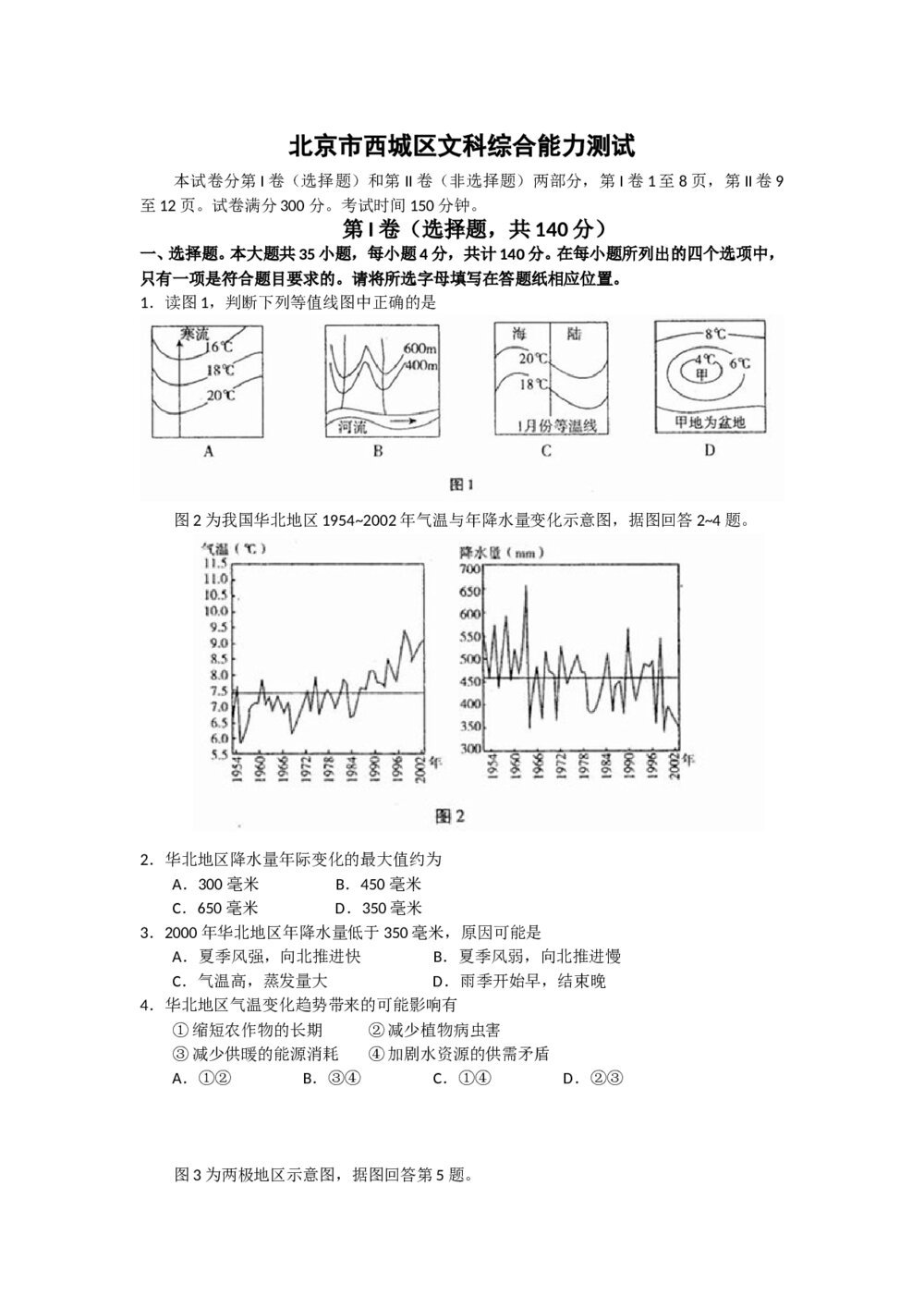 北京市西城区(文科)综合能力测试卷+参考答案
北京市西城区(文科)综合能力测试卷+参考答案 2015高三数学《文科》二轮复习《专题5 解析几何》PPT版
2015高三数学《文科》二轮复习《专题5 解析几何》PPT版 2011届高三一轮测试(文)8圆锥曲线方程+答案(通用版)
2011届高三一轮测试(文)8圆锥曲线方程+答案(通用版) 2011届高三一轮测试(理科)1集合与简易逻辑(1)(通用版)
2011届高三一轮测试(理科)1集合与简易逻辑(1)(通用版)