









《江苏省常州市常州中学2011-2012高三数学(文)最后冲刺综合练习试卷(二)》是由用户上传到老师板报网,本为文库资料,大小为277.5 KB,总共有10页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 10页
- 277.5 KB
- VIP模板
- doc
- 数字产品不支持退货
江苏省常州市常州中学2011-2012高三数学(文)最后冲刺综合练习试卷(二)一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在题中横线上.1.若复数2i1im,(Rmi是虚数单位)为纯虚数,则m=.2.若以连续掷两次骰子分别得到的点数m,n作为点P的坐标,则点P落在圆2216xy内的概率是.3.设等差数列na的前n项和为nS,若972S,则249aaa=.4.双曲线22163xy的渐近线与圆222(3)(0)xyrr相切,则r=.5.已知ABC中,3sin5A,8cos17B,则cosC=.6.某人5次下班途中所花的时间(单位:分钟)分别为m,n,5,6,4。已知这组数据的平均数为5,方差为2,则mn的值为.7.已知函数()fx满足:4x,则()fx=1()2x;当4x时()fx=(1)fx,则2(2log3)f=.8.已知函数1)32sin(4)(xxf,给定条件p:24x,条件q:2)(2mxf,若p是q的充分条件,则实数m的取值范围为.9.棱长为2的正四面体SABC中,M为SB上的动点,则AMMC的最小值为.10.以下有四种说法:(1)若pq为真,pq为假,则p与q必为一真一假;(2)若数列}{na的前n项和为*2,1NnnnSn,则*,2Nnnan;(3)若0)(0\'xf,则)(xf在0xx处取得极值;(4)若定义在R上的函数)(xf满足)1()2(xfxf,则6为函数)(xf的周期.以上四种说法,其中正确说法的序号为.11.已知椭圆C:2222byax=1(a>b>0)的左、右焦点分别为F1,F2.点M为椭圆C与直线20xy在第一象限的交点,平面上的点N满足21MFMFMN,过点(2,0)的直线l∥MN,则直线l的方程为.12.五位同学围成一圈依序循环报数,规定:①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;②若报出的数为3的倍数,则报该数的同学需拍手一次。当五位同学依序循环报数两圈时,拍手同学的总次数为.13.设函数()fxxxa,若对于任意21,xx21),,3[xx,不等式0)()(2121xxxfxf恒成立,则实数a的取值范围是.14.研究问题:“已知关于x的不等式02cbxax的解集为)2,1(,解关于x的不等式02abxcx”,有如下解法:解:由02cbxax0)1()1(2xcxba,令xy1,则)1,21(y,所以不等式02abxcx的解集为)1,21(.参考上述解法,已知关于x的不等式0cxbxaxk的解集为)3,2()1,2(,则关于x的不等式0111cxbxaxkx的解集为.二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)已知向量Rxxxxnxxm),cos32sin,(cos),sin,(cos,令nmxf)(,(1)当0,2x时,求()fx的值域;(2)已知2()23f,求2cos23的值.16.(本题满分14分)三棱柱111ABCABC中,面11BBCC面ABC,ABAC,D是BC的中点,M为1AA上一动点.(1)求证:1ADCC;(2)若1AMMA,求证:AD∥平面1MBC;(3)若面1MBC面11BBCC,求证:1AMMA.17.(本题满分16分)如图,F是椭圆12222byax(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为21.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:330xy相切.(1)求椭圆的方程:(2)过点A的直线l2与圆M交于PQ两点,且2MPMQ,求直线l2的方程.18.某地区1986年以来人口总数和居民住宅总面积分别按等比数列和等差数列逐年递增.已知1986年底人均住房面积为102m,2006年底人均住房面积为202m.据此计算:(1)1996年底人均住房面积超过142m,试给出证明;(2)若人口年平均增长率不超过3﹪,能否确保2008年底人均住房面积比2006年底有所增加?为什么?19.(本题满分16分)设数列na的前n和为nS,已知11,211,2,3,4nnaSnannn(1)求证:数列na为等差数列,并分别写出na和nS关于n的表达式;(2)设数列11nnaa的前n和为nT,证明:1154nT;(3)是否存在自然数n,使得232112009?23nSSSSnn若存在,求出的值;若不存在,请说明理由。20.(本题满分16分)已知32()2,()lnfxxaxxgxxx(1)如果函数()fx的单调递减区间为1,13,求函数()fx的解析式;(2)在(1)的条件下,求函数()yfx的图像过点P(1,1)的切线方程;(3)对一切的,0x,()22()fxgx恒成立,求实数a的取值范围.江苏省常州市常州中学2011-2012高三数学(文)最后冲刺综合练习试卷(二)参考答案:1、2;2、29;3、24;4、3;5、1385;6、6.;7、124;8、3,5;9、23;10、①④;11、220xy;12、3;13、3a;14、111(,)(,1)232题15、(1)()2sin(2)6fxx,∵0,2x,∴72666x1sin2,162x()yfx的值域为1,2;………………7分(2)221()2sinsin236363f227cos2cos2cos212sin3666914分.题16、(1)ABACBC,D为中点,ADBC1111又面BBCC面ABC,面BBCC面ABC=BC11ADBBCC面,又111CC面BBCC,1ADCC(2)延长1,CMCAPBP交于点,连结111111BPMBCAMAMAADBPADMBCCAAPDADMBC面为CP中点面为BC中点面(3)111111(1)ADBPADMBCDBCADBBCCMBCBPAD面BCP面MBC面BBCC面为中点由得面面BCP面111AAMMAAP为PC中点AC题17、(1)1,2,32ceacbca(,0),(0,3),(,0)FcBcCx设(,3),(,3)BCxcBFcc2,30,3BCBFcxcxc,BCBFM以CF为直径,M(c,0),r=2c1|3|2,12cMlcc与直线相切,22143xy椭圆方程为(2)2,22cos2MPMQPMQ01cos,1202PMQPMQ060,1PMNMN22,:(2),20lAlykxkxyk直线过点可设即222|3|21,91,41kkkkk,22:(2)4lyx题18、【解析】(1)设86年底人口总数为a,住宅总面积10a,年人口增长的公比为q(即后一年是前一年人口的q倍),年住宅总面积的公差为d,则2006年底人均住房面积为20102020adsaq,则20105(21)dqa,故1996年底人均住房面积201010101010525014adqAaqq.(2)2008年底人均住房面积2022221022221adqpaqq,2008年与2006年底人均住房面积之差2022222220120qqspq.∵0q,∴只需考虑分子2022202()222012(1110)1(1)fqqqqqq.∵1921()440()0fqqq,∴()fq单调递减.又2021.03()(1.03)21.03(11101.03)1qfqf≥≤,,∴2202011101.030.3921.032(10.03)2(1200.03)3.2,.∴()3.20.3910fq.此即表明,2008年底人均住房面积仍超过2006年底人均住房面积.题19(1)243,2nnanSnn;(2)122334111111414nnnnTaaaaaaaan,nT单调递增故11,5nTT所以1154nT(3)由22nSnn得21nsnn则2321123nnssssnn221nn21357211nn21n令212009n得1005n,所以存在满足条件的自然数1005n题20、(1)2()321fxxax由题意01232axx的解集是1,31即01232axx的两根分别是1,31将1x或31代入方程01232axx得1a,∴32()2fxxxx(2)设切点坐标是00,yxM10x.有1231102000xxxy将2020300xxxy代入上式整理得322000002420,210xxxxx即()得10x或00x.函数32()2fxxxx的图像过点P(1,1)的切线方程为02yx或1y.(3)由题意:232122lnxaxxx在,0x上恒成立即23212lnxaxxx可得xxxa2123ln设xxxxh2123ln,则22\'213121231xxxxxxh令0\'xh,得31,1xx(舍),当10x时,0\'xh;当1x时,0\'xh∴当1x时,xh取得最大值,xhmax=-2,.∴2a,即a的取值范围是,2.










 2017年高考理科数学三轮冲刺热点题型《12+4专项练4》+答案解析
2017年高考理科数学三轮冲刺热点题型《12+4专项练4》+答案解析 2020年高考真题数学统一试卷(文科)(新课标Ⅱ)(原卷版)
2020年高考真题数学统一试卷(文科)(新课标Ⅱ)(原卷版)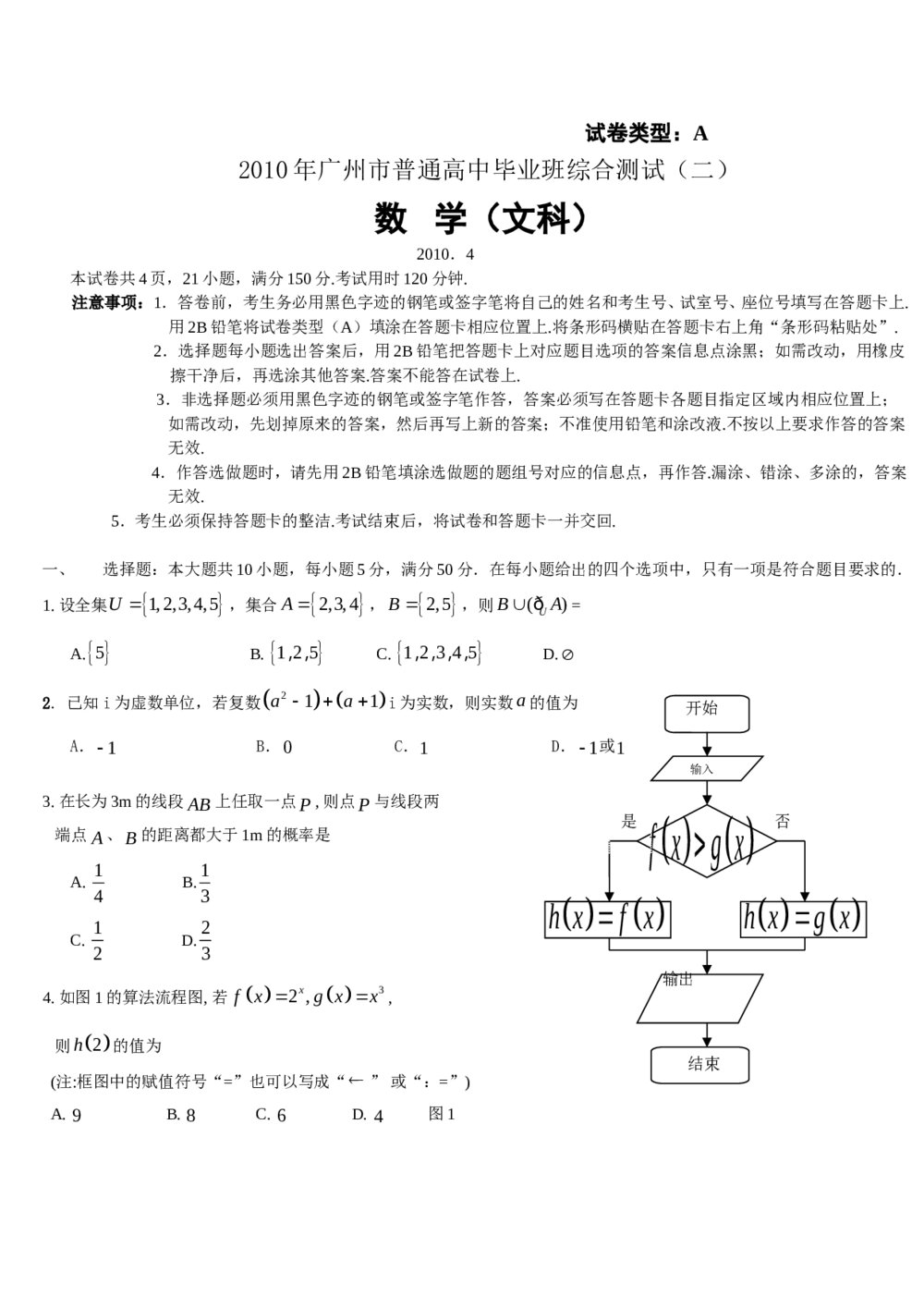 广州市高三二模数学(文科)试题+参考答案
广州市高三二模数学(文科)试题+参考答案 2011年高考一轮课时训练(理)7.4简单的线性规划问题+参考答案(通用版)
2011年高考一轮课时训练(理)7.4简单的线性规划问题+参考答案(通用版) 2020年高考海南省数学试卷(新高考全国Ⅱ卷)(解析版)
2020年高考海南省数学试卷(新高考全国Ⅱ卷)(解析版)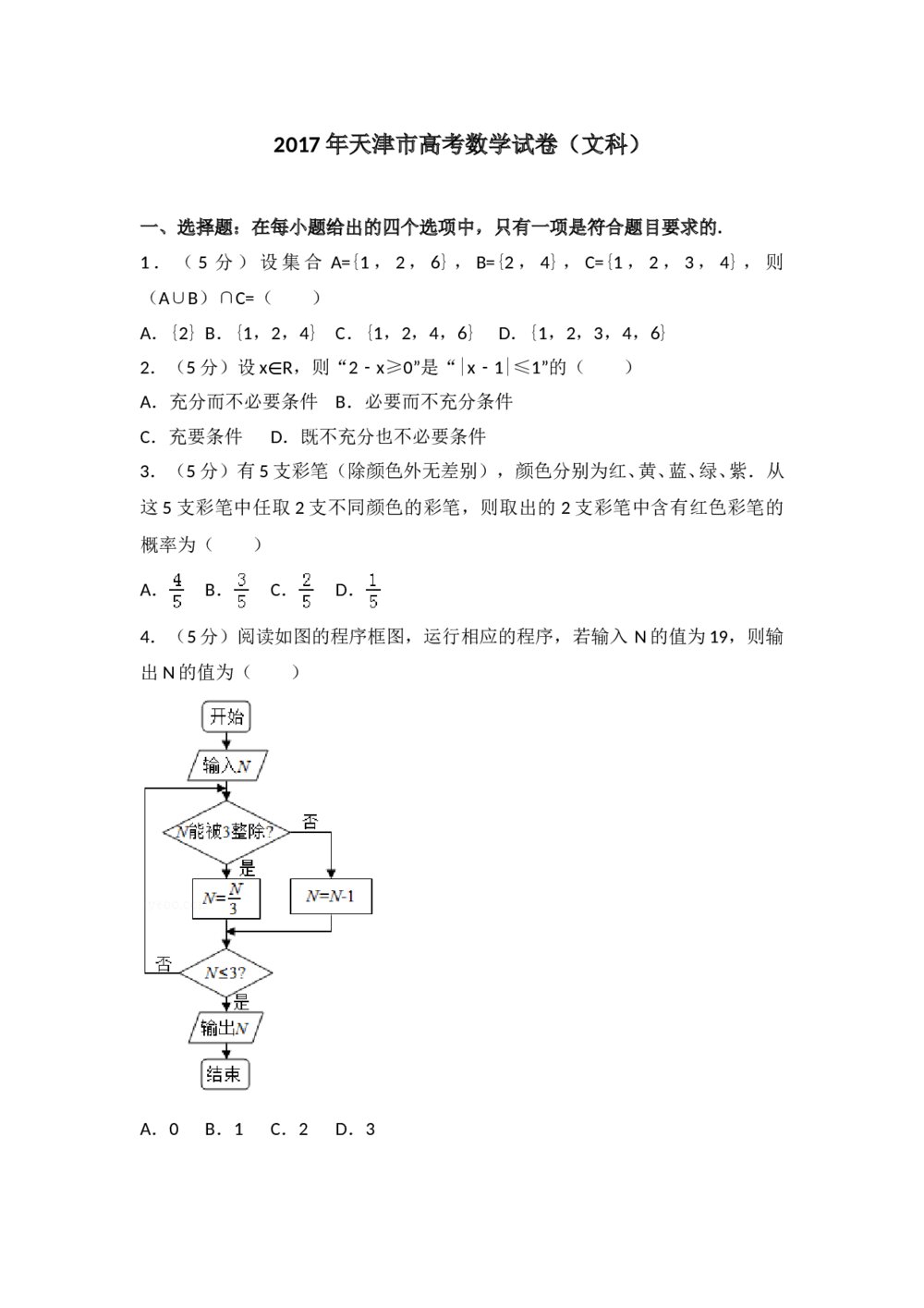 2017年天津高考数学(文科)试题试卷+参考答案(Word版)
2017年天津高考数学(文科)试题试卷+参考答案(Word版)