









《江苏省常州市常州中学2011-2012高三数学(文)最后冲刺综合练习试卷(一)》是由用户上传到老师板报网,本为文库资料,大小为282.5 KB,总共有10页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 10页
- 282.5 KB
- VIP模板
- doc
- 数字产品不支持退货
江苏省常州市常州中学2011-2012高三数学(文)最后冲刺综合练习试卷(一)一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在题中横线上.1.命题P:“对xA,都有2220xx.”则当[1,2]A时,命题P为命题(填“真”或“假”).2.在抽查某产品尺寸过程中,将其尺寸分成若干组,ba,是其中的一组,已知该组的频率为m,该组上的直方图的高为h,则ba等于.3.已知复数12312i,1i,32izzz,它们所对应的点分别为A,B,C.若OCxOAyOB,则xy的值是.4.函数sin(2)6yx为增函数的区间是 .5.设a、b分别是甲、乙各抛掷一枚骰子得到的点数.已知乙所得的点数为2,则方程20xaxb有两个不相等的实数根的概率为.6.若函数bbxxxf36)(3在)1,0(内有极小值,则实数b的取值范围是.7.有以下四个命题,其中正确命题的序号是.①“直线,ab为异面直线”的充分非必要条件是“直,ab不相交”;②“直线l⊥平面内的所有直线”的充要条件是“l”;③“直线ab”的充分非必要条件是“a垂直于b在内的射影”;④“直线a∥平面”的必要非充分条件是“直线a平行于内的一条直线”;8.椭圆12222byx的焦点为21,FF,两条准线与x轴的交点分别为,MN,若212FFMN,则该椭圆离心率取得最小值时的椭圆方程为 .9.已知点P的坐标(,)xy满足4,,1.xyyxx≤≥≥过点P的直线l与圆22:14Cxy交于A、B两点,求||AB最小值时的直线AB的方程.10.已知函数2()lg(3)fxxaxa,若对于任意的2,x,当0x时,恒有()()0fxfxxx,则实数a的取值范围是.11.路灯距地面为6m,一个身高为1.8m的人以0.8m/s的速度从路灯的正底下,沿某直线离开路灯,人影长度S(m)随人从路灯的正底下离开路灯的时间t()s的变化而变化,那么人影长度的变化速度v为(m/s).12.设函数21123()nnfxaaxaxax,1(0)2f,数列{}na满足2*(1)()nfnanN,则数列{}na的通项na等于.13.若不等式3260xax对任意xR恒成立,则实数a的取值范围是.14.设函数fx的定义域为R,若存在常数k0,使2010kfxx对一切实数x均成立,则称fx为“诚毅”函数.给出下列函数:①2fxx;②fxsinxcosx;③21xfxxx;④31xfx;其中fx是“诚毅”函数的序号为.二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)如图,已知空间四边形ABCD中,O是对角线BD的中点,2,2.CACBCDBDABAD(1)求证:COAO;(2)求证:AO平面BCD;(3)若G为ADC的重心,试在线段DO上确定一点F,使得//GFAOC平面.16.(本题满分14分)已知ABC中,角A,B,C,所对的边分别是,,abc,且22223abcab;(1)求2sin2AB;(2)若2c,求ABC面积的最大值.17.(本题满分16分)在平面直角坐标系xOy中,已知以O为圆心且面积最小的圆与直线l:(34)ymxm()mR恒有公共点T.(1)求出T点的坐标及圆O的方程;(2)圆O与x轴相交于A、B两点,圆内动点P使||PA、||PO、||PB成等比数列,求PAPB的范围;(3)设点T关于y轴的对称点为Q,直线l与圆O交于M、N两点,试求QQtanQSMNMN的最大值,并求出S取最大值时的直线l的方程.18.某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.(I)写出y与x之间的函数关系式;(II)从第几年开始,该机床开始盈利(盈利额为正值)(III)使用若干年后,对机床的处理方案有两种:(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;(2)当盈利额达到最大值时,以12万元价格处理该机床.问用哪种方案处理较为合理?请说明理由.19.(本题满分16分)已知函数1)(23cxbxxxf在区间2,上单调递增,在区间23,2上单调递减,若b是非负整数,(1)求)(xf的表达式;(2)设20m,若对任意的mmtt,2,21,不等式mtftf16)()(21恒成立,求实数m的最小值.20.(本题满分16分)已知正项数列na的首项1am,其中01m,函数()1xfxx.(1)若正项数列na满足1()(1)nnafannN且,证明1na是等差数列,并求出数列na的通项公式;(2)若正项数列na满足1()(1)nnafannN且,数列nb满足1nnabn,试证明:121nbbb.江苏省常州市常州中学2011-2012高三数学(文)最后冲刺综合练习试卷(一)参考答案:1、真;2、mh;3、5;4、5,36kk;5、23;6、;)21,0(7、②④;8、1222yx;9、3100xy;10、4,4;11、1235;12、1(1)nn;13、3,;14、③;15.证明:(1)连结OC、OA,,.BODOABADAOBD,,.BODOBCCDCOBD在AOC中,由已知可得1,3.AOCO而2,AC222,AOCOAC90,oAOC即.AOOC………5分(2),AOOCAOBD,,BDOCOAO平面BCD………8分(3)连结DG并延长交AC于H,则13DGDH,在DO上取点F,使13DFDO,连结FG、OH//DGDFFGOHDHDOOH平面AOC,FG平面AOC//GFAOC平面…14分16.解:(Ⅰ)22222233,cos224abcabcabCab21cos1cos7,sin2228ABABCABC………………6分(Ⅱ)ab,ba,cabcba2342,2322222且又2232,24,82ababababab22337cos,sin1cos1444CCC,7sin21CabSABC当且仅当22ba时,△ABC面积取最大值,最大值为7.…………14分17.解:(1)因为直线l:(34)ymxm过定点T(4,3)……… 2分由题意,要使圆O的面积最小,定点T(4,3)在圆上,所以圆O的方程为2225xy;……… 5分(2)A(-5,0),B(5,0),设00(,)Pxy,则220025xy……(1)00(5,)PAxy,00(5,)PBxy,由||,||,||PAPOPB成等比数列得,2||||||POPAPB,即222222000000(5)(5)xyxyxy,整理得:2200252xy,即2200252xy……(2)由(1)(2)得:202504y,22200025(25)22PAPBxyy,25[,0)2PAPB10分(3)tan||||costanQMQNMQNQMQNMQNMQN||||sin2MQNQMQNMQNS,……… 11分由题意,得直线l与圆O的一个交点为M(4,3),又知定点Q(4,3),直线MQl:3y,||8MQ,则当(0,5)N时MQNS有最大值32.……… 14分即tanQMQNMQN有最大值为32,此时直线l的方程为250xy.… 16分18.解:(I)依题得:2*(1)501249824098.()2xxyxxxxxN(II)解不等式2240980,:10511051xxx得*,317,3xNx故从第年开始盈利。(III)(1)989824040(2)40229812yxxxxx当且仅当982xx时,即x=7时等号成立.到2015年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.(2)2224098(10)102,10102yxxxmax当x=时,y故到2018年,盈利额达到最大值,工厂获利102+12=114万元因为盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理19.解:/2()32fxxbxc函数f(x)在区间2,上单调递增,在区间23,2上单调递减,/()1240,fxbc即412cb………………………………………3分/3()02f,328210,4bbb是非负整数,0b,………6分从而12c,所以3()121fxxx……………………8分(2)/()3(2)(2)fxxx,()fx在2,2上单调递减,在2,上单调递增02,220mm()fx在2,mm上单调递减maxmin()(2),()()fxfmfxfm…………………………………………12分依题意maxmin()()16fxfxm即23280mm423mm或402,23mm所以,m的最大值为43…………………16分20.解:(1)依题目条件有11111(1,)1nnnnnaannNaaa所以数列1na是以111am为首项,1为公差的等差数列,所以11(1)1nnam,即1(1)nmanm.……………………………4分(2)由条件可知,1,0(1)1nnnnaaannNa且1111kkaa,即1111,2,3,,,kkknaa21111,aa32111,aa1111,nnaa叠加可得1111nnaa,而1,(1,)1(1)nmamannNnm11101,1,1,2,,,11kmaknmkkm111,1,2,,,1(1)1kkabknkkkkk12111111(1)()()112231nbbbnnn,得证…………16分.展开内容










 20以内数字加减法练习(word版)
20以内数字加减法练习(word版)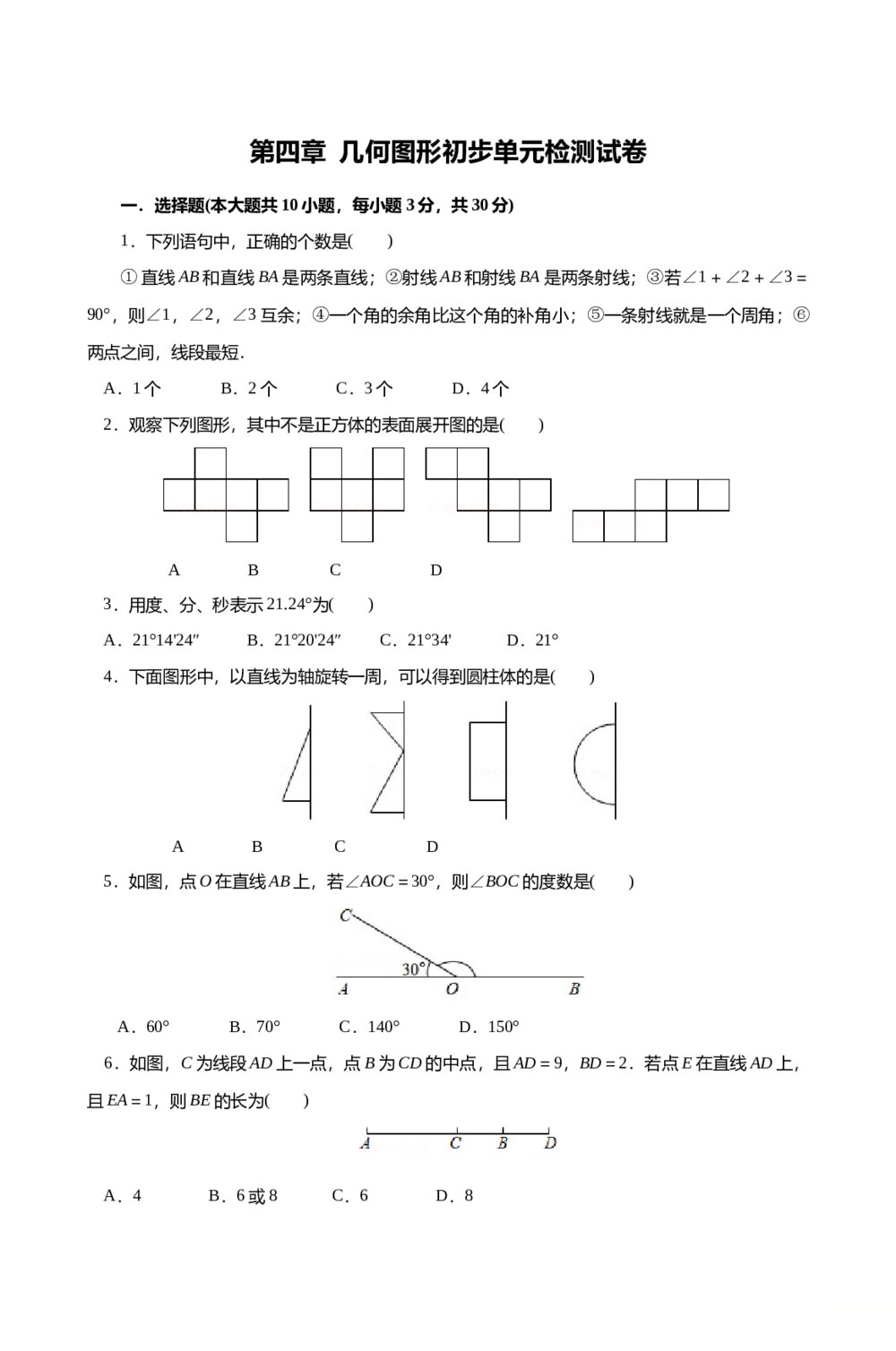 人教版七年级数学上册《第四章·几何图形初步单元检测试卷》+(含参考答案)
人教版七年级数学上册《第四章·几何图形初步单元检测试卷》+(含参考答案) 北京市石景山区高三一模数学文科+参考答案
北京市石景山区高三一模数学文科+参考答案 2011年全国统一高考数学试卷(理科)(大纲版)+(答案解析)
2011年全国统一高考数学试卷(理科)(大纲版)+(答案解析) 重庆卷2011全国高考(理科)数学试卷
重庆卷2011全国高考(理科)数学试卷 小学二年级数学应用题专项训练word
小学二年级数学应用题专项训练word