









试读已结束,还剩4页未读,您可下载完整版后进行离线阅读
《北京2012年高考数学(理科)试题试卷+答案》是由用户上传到老师板报网,本为文库资料,大小为591.5 KB,总共有14页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 14页
- 591.5 KB
- VIP模板
- doc
- 数字产品不支持退货
北京2012届高考预测试卷数学理试题第Ⅰ卷为选择题,共60分;第Ⅱ卷为非选择题共90分。满分100分,考试时间为120分钟。第Ⅰ卷(选择题,共60分)一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.1.已知集合012A,,,集合2Bxx,则AB()A.2B.012,,C.2xxD.2.已知i是虚数单位,则ii221等于()A.iB.i54C.i5354D.i3.一个几何体的三视图如图所示,则该几何体的体积为()A.12B.11C.312D.3114.若数列{}na的前n项和为nS,则下列命题:(1)若数列{}na是递增数列,则数列{}nS也是递增数列;(2)数列{}nS是递增数列的充要条件是数列{}na的各项均为正数;(3)若{}na是等差数列(公差0d),则120kSSS的充要条件是120.kaaa(4)若{}na是等比数列,则120(2,)kSSSkkN的充要条件是10.nnaa其中,正确命题的个数是()A.0个B.1个C.2个D.3个5.如图,长方形的四个顶点为)2,0(),2,4(),0,4(),0,0(CBAO,曲线xy经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是()A.125B.21C.32D.436.已知:命题p:“1a是2,0xaxx的充分必要条件”;命题q:“02,0200xxRx”.则下列命题正确的是()A.命题“p∧q”是真命题B.命题“(┐p)∧q”是真命题C.命题“p∧(┐q)”是真命题D.命题“(┐p)∧(┐q)”是真命题7.若空间三条直线a、b、c满足,//abbc,则直线ac与()A.一定平行B.一定相交C.一定是异面直线D.一定垂直8.函数xxyln的图象大致是()9.如图所示的方格纸中有定点OPQEFGH,,,,,,,则OPOQ()A.OHB.OGC.FOD.EO10.设22)1(则,3005满足约束条件,yxxyxyxyx的最大值为()A.80 B.45 C.25 D.17211.若双曲线222(0)xyaa的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α,β,且(1)mm,那么α的值是()A.21mB.2mC.21mD.22m12.若实数t满足ftt(),则称t是函数fx()的一个次不动点.设函数lnfxx()与函数exgx()(其中e为自然对数的底数)的所有次不动点之和为m,则()A.0mB.0mC.01mD.1m第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。13.431xx展开式中常数为;14.在ABC中,已知abc,,分别为A,B,C所对的边,S为ABC的面积.若向量22241pabcqS()(),,,满足//pq,则C=.15.执行如图的程序框图,那么输出S的值是;16、已知213cos,4152cos5cos,231coscoscos7778,。根据以上等式,可猜想出的一般结论是;三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知函数23sincossin2424xxfxx()()()().(Ⅰ)求fx()的最小正周期;(Ⅱ)若将fx()的图象向右平移6个单位,得到函数gx()的图象,求函数gx()在区间0[,]上的最大值和最小值.18.(本小题满分12分)在一次数学考试中,第21题和第22题为选做题.规定每位考生必须且只须在其中选做一题.设4名考生选做这两题的可能性均为12.(Ⅰ)求其中甲、乙二名学生选做同一道题的概率;(Ⅱ)设这4名考生中选做第22题的学生个数为,求的概率分布及数学期望。20419.(本小题满分12分)如图,AC是圆O的直径,点B在圆O上,30BAC,BMAC交AC于点M,EA平面ABC,//FCEA,431ACEAFC,,.(Ⅰ)证明:EMBF;(Ⅱ)求平面BEF与平面ABC所成的锐二面角的余弦值.20.(本小题满分12分)已知数列}2{1nna的前n项和96nSn.(Ⅰ)求数列{na}的通项公式;(Ⅱ)设2(3log)3nnabn,求数列{1nb}的前n项和.21.(本小题满分12分)直线l与椭圆22221(0)yxabab交于11(,)Axy,22(,)Bxy两点,已知m),(11byax,n),(22byax,若nm且椭圆的离心率32e,又椭圆经过点3(,1)2,O为坐标原点.ABCEFMO(Ⅰ)求椭圆的方程;(Ⅱ)若直线l过椭圆的焦点(0,)Fc(c为半焦距),求直线l的斜率k的值;(Ⅲ)试问:AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由。22.(本小题满分14分)已知函数ln1afxxaxR()().(Ⅰ)当92a时,如果函数gxfxk()()仅有一个零点,求实数k的取值范围;(Ⅱ)当2a时,试比较fx()与1的大小;(Ⅲ)求证:1111ln135721nn()n*N().参考答案一.选择题1、D;2、A;3、A;4、B;5、C;6、B;7、D;8、C;9、C;10、A;11、D;12、B;二.填空题13、—4;14、4;15、21;16、21coscoscos2121212nnnnn,nN。三.解答题17.解析:(Ⅰ)xxxfsin)2sin(3)(xxsincos3…………………2分)cos23sin21(2xx)3sin(2x.……………………………4分所以)(xf的最小正周期为2.………………………………………6分(Ⅱ)将)(xf的图象向右平移6个单位,得到函数)(xg的图象,3)6(sin2)6()(xxfxg)6sin(2x.…………………8分[0,]x时,]67,6[6x,…………………………………………………9分当26x,即3x时,sin()16x,)(xg取得最大值2.…………10分当766x,即x时,1sin()62x,)(xg取得最小值1.………12分18.解析:(Ⅰ)设事件A表示“甲选做第21题”,事件B表示“乙选做第21题”,则甲、乙2名学生选做同一道题的事件为“ABAB”,且事件A、B相互独立∴()()()()()PABABPAPBPAPB=11111(1)(1)22222.……………6分(Ⅱ)随机变量的可能取值为0,1,2,3,4,且~1(4,)2B.∴4444111()()(1)()(0,1,2,3,4)222kkkkPkCCk∴变量的分布表为:113110123421648416E…………………………12分19.解析:(法一)(Ⅰ)EA平面ABC,BM平面ABC,BMEA.………………………………………………………………………………1分又AC,BMAACEA,BM平面ACFE,而EM平面ACFE,EMBM.……………………………………………………………………………3分AC是圆O的直径,90ABC.又,BAC304AC,,BC,AB2321,3CMAM.EA平面ABC,EAFC//,1FC,FC平面ABCD.EAM与FCM都是等腰直角三角形.45FMCEMA.90EMF,即MFEM(也可由勾股定理证得).………………………………5分MBMMF,EM平面MBF.而BF平面MBF,EMBF.………………………………………………………………………………6分(Ⅱ)延长EF交AC于G,连BG,过C作CHBG,连结FH.由(1)知FC平面ABC,BG平面ABC,FCBG.而FCCHC,BG平面FCH.FH平面FCH,FHBG,FHC为平面BEF与平面ABC所成的二面角的平面角.……………………8分01234P116143814116HGABCEFMO在ABCRt中,30BAC,4AC,330sinABBM.由13FCGCEAGA,得2GC.3222MGBMBG.又GBMGCH~,BMCHBGGC,则13232BGBMGCCH.………………………………11分FCH是等腰直角三角形,45FHC.平面BEF与平面ABC所成的锐二面角的余弦值为22. ………………………12分(法二)(Ⅰ)同法一,得33BMAM,.………………………3分如图,以A为坐标原点,垂直于AC、AC、AE所在的直线为zyx,,轴建立空间直角坐标系.由已知条件得(0,0,0),(0,3,0),(0,0,3),(3,3,0),(0,4,1)AMEBF,(0,3,3),(3,1,1)MEBF.………4分由(0,3,3)(3,1,1)0MEBF,得BFMF,BFEM.……………6分(Ⅱ)由(1)知(3,3,3),(3,1,1)BEBF.设平面BEF的法向量为),,(zyxn,由0,0,nBEnBF得333030xyzxyz,令3x得1,2yz,3,1,2n,…………………………9分由已知EA平面ABC,所以取面ABC的法向量为(0,0,3)AE,xyzABCEFMO设平面BEF与平面ABC所成的锐二面角为,则3010232coscos,2322nAE,…………………………11分平面BEF与平面ABC所成的锐二面角的余弦值为22.……………………12分20.解析:(Ⅰ)1n时,011123,3aSa;……………………………………2分11232,26,2nnnnnnnaSSa时.………………………………………4分 23(1)3(2)2nnnan通项公式……………………………………………6分(Ⅱ)设1nnnTb的前项和为,当1n时,1211113log13,3bTb;…………………………………7分 2n时,223(3log)(1)32nnbnnn,1nb1(1)nn……………10分nT1211111132334nbbb1(1)nn=5161n……………12分21.解析:(Ⅰ)∵2222321314cabeaaab…………………2分∴2,1ab∴椭圆的方程为2214yx………………3分(Ⅱ)依题意,设l的方程为3ykx由22223(4)231014ykxkxkxyx显然0121222231,44kxxxxkk………………5分由已知nm0得:22121212124(3)(3)axxbyyxxkxkx21212(4)3()3kxxkxx222123k(k4)()3k30k4k4解得2k……………………6分(Ⅲ)①当直线AB斜率不存在时,即2121,xxyy,由已知nm0,得22221111404xyyx又11(,)Axy在椭圆上,所以221111421||,||242xxxy1121111||||||2||122Sxyyxy,三角形的面积为定值.………7分②当直线AB斜率存在时:设AB的方程为ykxt22222(4)24014ykxtkxktxtyx必须0即222244(4)(4)0ktkt得到12224ktxxk,212244txxk………………9分∵nm,∴12121212404()()0xxyyxxkxtkxt代入整理得:2224tk…………………10分2121121||1||||()4221tSABtxxxxk…………11分2222||44164142||tkttkt所以三角形的面积为定值.…………………12分22.解析:(Ⅰ)当29a时,)1(29ln)(xxxf,定义域是),0(,22)1(2)2)(12()1(291)(xxxxxxxf,令0)(xf,得21x或2x.…2分当210x或2x时,0)(xf,当221x时,0)(xf,函数)(xf在)21,0(、),2(上单调递增,在)2,21(上单调递减.……………4分)(xf的极大值是2ln3)21(f,极小值是2ln23)2(f.当0x时,)(xf;当x时,)(xf,当)(xg仅有一个零点时,k的取值范围是2ln3k或2ln23k.……………5分(Ⅱ)当2a时,12ln)(xxxf,定义域为),0(.令112ln1)()(xxxfxh,0)1(1)1(21)(222xxxxxxh,)(xh在),0(上是增函数.…………………………………7分①当1x时,0)1()(hxh,即1)(xf;②当10x时,0)1()(hxh,即1)(xf;③当1x时,0)1()(hxh,即1)(xf.…………………………………9分(Ⅲ)(法一)根据(2)的结论,当1x时,112lnxx,即11lnxxx.令kkx1,则有1211lnkkk,nknkkkk111211ln.……………12分nkkkn11ln)1ln(,1215131)1ln(nn.……………………………………14分(法二)当1n时,ln(1)ln2n.3ln2ln81,1ln23,即1n时命题成立.………………………………10分设当nk时,命题成立,即111ln(1)3521kk.1nk时,2ln(1)ln(2)ln(1)ln1knkkk1112ln35211kkk.根据(Ⅱ)的结论,当1x时,112lnxx,即11lnxxx.令21kxk,则有21ln123kkk,则有1111ln(2)352123kkk,即1nk时命题也成立.……………13分因此,由数学归纳法可知不等式成立.………………………………14分(法三)如图,根据定积分的定义,得1121171151nndxx1121.……11分)12(1212112111xdxdxxnnxyo123456n-1n…]3ln)12[ln(21)12ln(211nxn,121715131n)12151(31nndxx112131]3ln)12[ln(2131n.………………………………12分11[ln(21)ln3]ln(1)32nn223ln31[ln(21)ln(21)]62nnn,又3ln332,)12ln()12ln(2nnn,)1ln(]3ln)12[ln(2131nn.)1ln(1215131nn.…………………………………14分










 2012高考数学备考冲刺之易错点点睛系列专题《数列》学生版
2012高考数学备考冲刺之易错点点睛系列专题《数列》学生版 2011年高考一轮课时训练(理)16.2.1坐标系+参考答案(通用版)
2011年高考一轮课时训练(理)16.2.1坐标系+参考答案(通用版) 2012年江苏省高考数学一轮训练试题考点8《选修系列四》
2012年江苏省高考数学一轮训练试题考点8《选修系列四》 三年级数学期末试卷考试word
三年级数学期末试卷考试word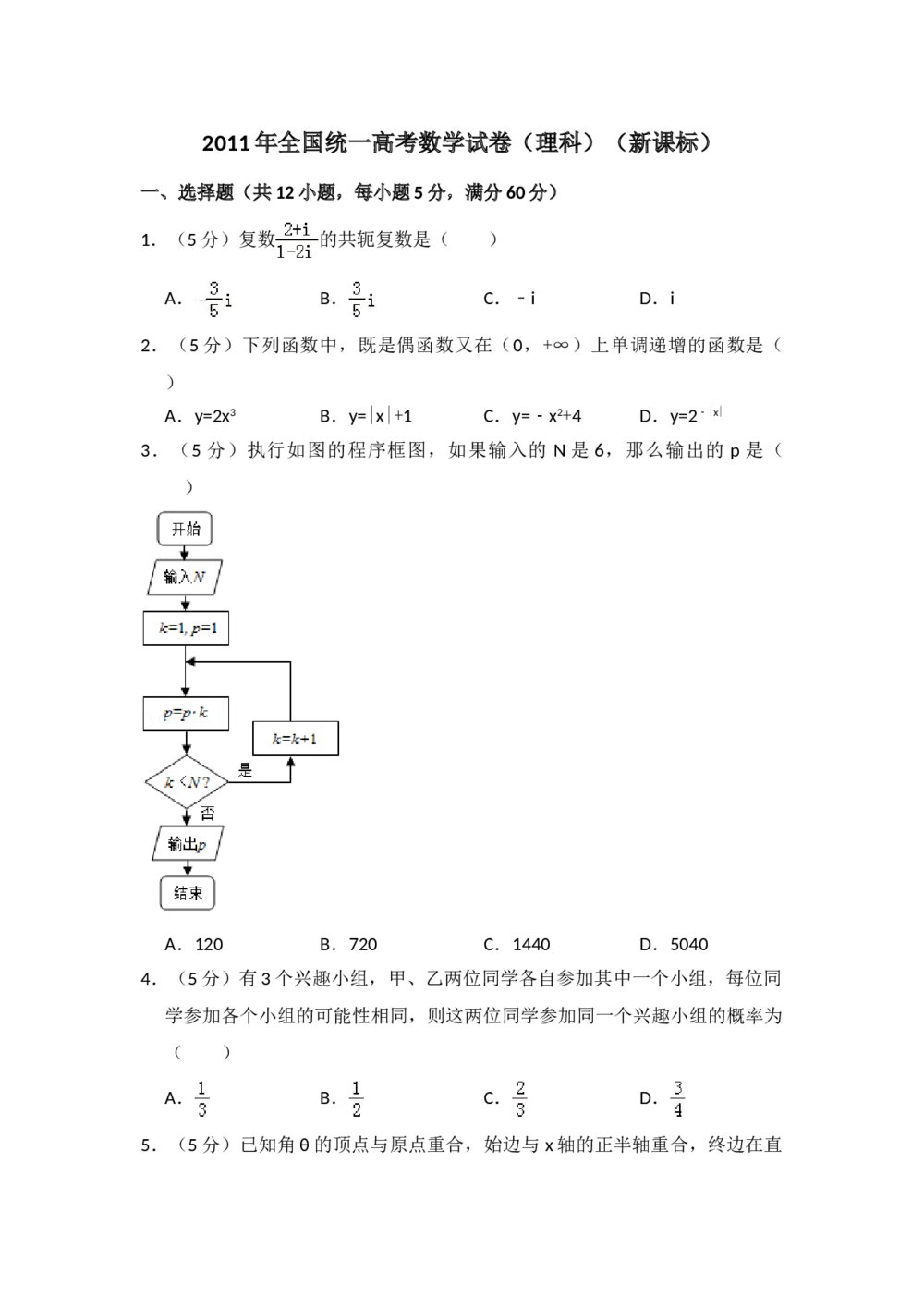 2011年全国统一高考数学试卷(理科)(新课标)+(答案解析)
2011年全国统一高考数学试卷(理科)(新课标)+(答案解析) 2012湖北卷(文科)数学试题+参考答案
2012湖北卷(文科)数学试题+参考答案