



《2011年高考一轮课时训练(理)16.2.1坐标系+参考答案(通用版)》是由用户上传到老师板报网,本为文库资料,大小为141 KB,总共有4页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 4页
- 141 KB
- VIP模板
- doc
- 数字产品不支持退货
第二讲 坐标系与参数方程第一节 坐标系题号12345答案一、选择题1.把点P的直角坐标(,-)化为极坐标为( )A. B.C.D.2.已知点A的极坐标为,则它的直角坐标是( )A.(1,)B.(1,-)C.(-1,)D.(-1,-)3.在平面直角坐标系中,抛物线x2=-3y经过伸缩变换后得到的曲线是( )A.y′2=-4x′B.x′2=-4y′C.y′2=-x′D.x′2=-y′4.在极坐标系中,ρ1=ρ2且θ1=θ2是两点M(ρ1,θ1)和N(ρ2,θ2)重合的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.如右图所示,棱长为1的正方体在的球坐标系中,顶点F的坐标可用有序数对(ρ,θ,φ)表示,则( )A.ρ=2B.θ=C.cosθ=D.φ=二、填空题6.已知点A的极坐标是,则满足条件ρ>0,-2π<θ<0的点A的极坐标是________.7.极坐标为的点M的直角坐标是________.8.在同一平面直角坐标系中,直线x-2y=2变成直线2x′-y′=4.则满足上述图形变换的伸缩变换是________.三、解答题9.如右图所示,用点A,B,C,D,E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置.建立适当的极坐标系,写出各点的极坐标.10.在同一平面直角坐标系中,求满足以下图形变换的伸缩变换:曲线x2-y2-2x=0变成曲线x′2-16y′2-4x′=0.参考答案1.C2.解析:直接代入公式,即得答案:C3.解析:由伸缩变换,得到.代入x2=-3y,得到经过伸缩变换后的图形是(2x′)2=-3·(3y′),即x′2=-y′.故选D.答案:D4.解析:若ρ1=ρ2且θ1=θ2,则两点M(ρ1,θ1)和N(ρ2,θ2)为同一点,一定重合;反之,由于点的极坐标的多样性,若M(ρ1,θ1)和N(ρ2,θ2)两点重合,但ρ1=ρ2且θ1=θ2不一定成立.所以,ρ1=ρ2且θ1=θ2是两点M(ρ1,θ1)和N(ρ2,θ2)充分不必要条件.故选A.答案:A5.解析:以正方体的一个顶点为极点,相邻的两条棱所在的射线分别为Ox轴和Oz轴,建立如右图所示的球坐标系.则有OF=,cosθ===,tanφ=1,故选C.答案:C6.解析:由于同一点的极坐标有无数种表示形式,所以,先写出点的一般形式,后写出符合条件的形式.当ρ>0时,点A的极坐标的一般形式是(k∈Z).由-2π<θ<0,得-2π<+2kπ<0,解得,k=-1,则θ=-.即满足条件的点A的极坐标是.答案:7.解析:因为ρ=,θ=π,代入极坐标与直角坐标的互化公式,得x=·cosπ=-,y=·sinπ=0.所以点M的直角坐标是.答案:8.解析:依照伸缩变换公式,用待定系数法求解.设伸缩变换为代入2x′-y′=4得 2λx-μy=4.将上述与x-2y=2即2x-4y=4比较,得λ=1,μ=4.故所求的伸缩变换为答案:9.解析:以A为极点,AB所在射线为极轴(单位长度为1m),建立如题图所示的极坐标系.容易知道,点A,B,C,D,E的极坐标是:(0,0),(60,0),,,.10.解析:根据伸缩变换公式,用待定系数法求解.设伸缩变换为代入x′2-16y′2-4x′=0,得(λx)2-16(μy)2-4λx=0,即 λ2x2-16μ2y2-4λx=0.将上式与x2-y2-2x=0相比较,得==,解得λ=2,μ=.因而所求的伸缩变换是展开内容




 2012山东卷高考数学(理科)试卷
2012山东卷高考数学(理科)试卷 最新6年高考4年模拟试题试卷--第六章第二节数列的应用(答案解析)
最新6年高考4年模拟试题试卷--第六章第二节数列的应用(答案解析)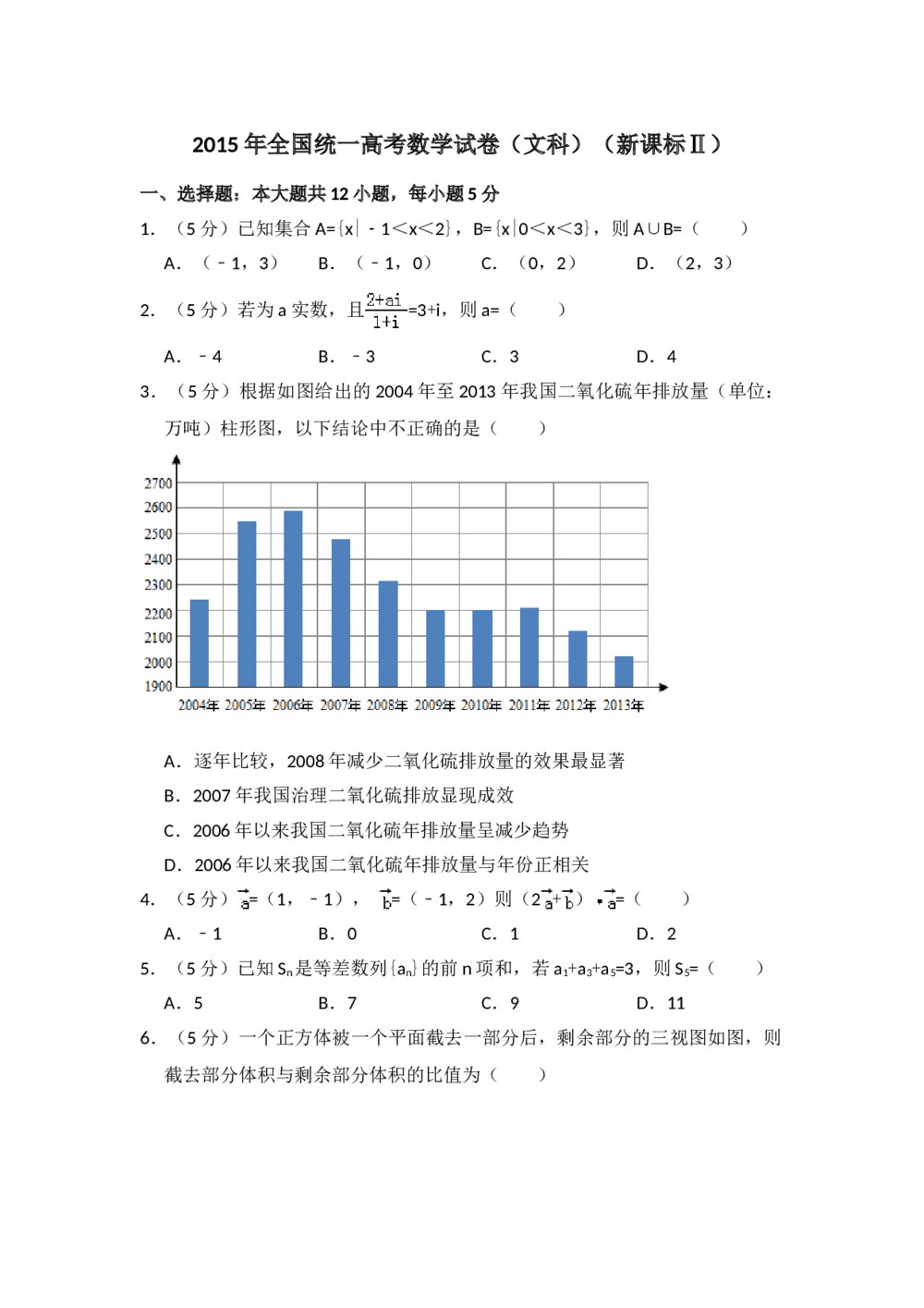 2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析
2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析 2020年全国统一高考数学(文科)试卷新课标Ⅱ)(原卷版)
2020年全国统一高考数学(文科)试卷新课标Ⅱ)(原卷版) 2016年高考(文科)数学试卷(新课标Ⅱ)+(答案)
2016年高考(文科)数学试卷(新课标Ⅱ)+(答案) 高中数学《几何概型》word学案
高中数学《几何概型》word学案