






《2012年江苏省高考数学一轮训练试题考点8《选修系列四》》是由用户上传到老师板报网,本为文库资料,大小为466.5 KB,总共有7页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 7页
- 466.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2010-2011学年度第一学期南通市六所省重点高中联考试卷数学Ⅱ试题(附加题)一、选答题:本大题共4小题,请从这4题中选做两小题,如果多做,则按所做的前两题记分,每小题10分,共20分,请在答题卡指定区域内作答,解答应写出文字说明,证明步骤或演算步骤.1.(选修4—1:几何证明选讲)如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.(1)求证:2PMPAPC;(2)若⊙O的半径为23,OA=3OM,求MN的长.解:(1)由条件得矩阵2003M,它的特征值为2和3,对应的特征向量为10及01;………5分(2)1102103M,椭圆22149xy在1M的作用下的新曲线的方程为221xy.…10分2.(选修4—2:矩阵与变换)设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.(1)求矩阵M的特征值及相应的特征向量;(2)求逆矩阵1M以及椭圆22149xy在1M的作用下的新曲线的方程.3.(选修4—4:不等式选讲)设a,b,c均为正实数.(1)若1abc,求222abc的最小值;(2)求证:111111222abcbccaab≥.4.(选修4—4:坐标系与参数方程)已知椭圆的长轴长为6,焦距2421FF,过椭圆左焦点F1作一直线,交椭圆于两点M、N,设OCMNAPB(第1题))0(12MFF,当α为何值时,MN与椭圆短轴长相等?(用极坐标或参数方程方程求解)解:以椭圆的左焦点为极点长轴所在直线为极轴建立极坐标系(如图)这里:a=3,c=322,42,1,222eccapb,………………………2分所以椭圆的极坐标方程为:cos2231cos1eep………………………4分设M点的极坐标为),(1,N点的极坐标为),(2,………………5分12222116,98cos322cos322cos()63352cos,cos,0.10426698cosMNMN由得,又,所以或分解法二:设椭圆的方程为1922yx,其左焦点为)0,22(,直线MN的参数方程为:为参数)llylx(sincos22,………………4分将此参数方程代人椭圆方程并整理得:分或分10656,0(,21sin,41sin82sin816sin81)sin81(4cos322222221ttMN01cos24)sin81(22tt,设M、N对应的参数分别为21tt、,则2011届江苏省苏州市迎二模六校联考数学试题数学附加题,选做题21.A.选修4—1:(几何证明选讲)如图,AD是∠BAC的平分线,⊙O过点A且与BC边相切于点D,与AB,AC分别交于E,F,求证:EF∥BC.证明:如图,连结DF.因为BC与圆相切,所以∠CDF=∠DAF.…………………………4分因为∠EFD与∠EAD为弧DE所对的圆周角,所以∠EFD=∠EAD.又因为AD是∠BAC的平分线,故∠EAD=∠DAF.…………………………8分所以∠CDF=∠EFD,所以EF∥BC.…………………………10分B.选修4—2:(矩阵与变换)已知a,b∈R,若矩阵M=所对应的变换把直线l:2x-y=3变换为自身,求F1F2xαMNABDCEFO·a,b的值.解:(方法一)在直线l上取两点(,0),(0,-3).因为=,=,………………………6分因为M对应的变换把直线变换为自身,所以点(-,b),(-3a,-9)仍在直线l上.代入直线方程得解得………………………10分(方法二)设(x,y)为直线l上任意一点,则=,…………………………3分因为M对应的变换把直线变换为自身,所以点(-x+ay,bx+3y)仍在直线l上,代入直线方程得:2(-x+ay)-(bx+3y)=3,…………………………7分化简得(-2-b)x+(2a-3)y=3,又直线l:2x-y=3,所以解得…………………………10分C.选修4—4:(坐标系与参数方程)将参数方程(t为参数)化为普通方程.解:(方法一)因为(t+)2-(t-)2=4,…………………………5分所以()2-()2=4.…………………………8分化简得普通方程为-=1.…………………………10分(方法二)因为,所以t=,=,…………………………5分相乘得=1.…………………………8分化简得普通方程为-=1.…………………………10分D.选修4—5:(不等式选讲)已知a,b是正数,求证(a+)(2b+)≥.证明:(方法一)因为a,b是正数,利用均值不等式,(a+)(2b+)=2ab++2+…………………………5分=(2ab+)+≥2+=.所以(a+)(2b+)≥.…………………………10分(方法二)因为a,b是正数,利用柯西不等式,(a+)(2b+)=[()2+()2][()2+()2]……………………5分≥(×+×)2=(+)2=.所以(a+)(2b+)≥.………………………10分江苏省2011届高三上学期苏北大联考(数学)数学Ⅱ试题(附加题)1、已知矩阵dcA33,若矩阵A属于特征值6的一个特征向量为111α,属于特征值1的一个特征向量为232α.求矩阵A,并写出A的逆矩阵.解:由矩阵A属于特征值6的一个特征向量为111可得,3311611cd,即c+d=6;………………………………………2分由矩阵A属于特征值1的一个特征向量为232,可得333322cd,即3c-2d=-2,…………………………………………6分解得233424cAa…………………………8分A的逆矩阵12/31/21/31/2Ac2、过点P(-3,0)且倾斜角为30°直线和曲线1,()1xtttytt为参数相交于A、B两点.求线段AB的长.解:直线的参数方程为33,2()12xssys为参数,…………………………3分曲线1,()1xtttytt为参数可以化为224xy.……………………………5分将直线的参数方程代入上式,得263100ss.设A、B对应的参数分别为12ss,,∴12126310ssss,.……………8分AB2121212()4ssssss=217.…………………………………10分2011年江苏省海安高级中学、南京外国语学校、南京市金陵中学高三调研测试数学(加试部分)21.【选做题】在A、B、C、D四小题中只能选做两题,每小题l0分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A.选修4–1几何证明选讲BCEDAABCDDFO如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC交于点D.求证:ED2=EB·EC.B.矩阵与变换已知矩阵2143A,4131B,求满足AXB的二阶矩阵X.C.选修4–4参数方程与极坐标若两条曲线的极坐标方程分别为=1与=2cos(+),它们相交于A,B两点,求线段AB的长.D.选修4–5不等式证明选讲设a,b,c为正实数,求证:a3+b3+c3+≥2.江苏省常州市2011届高三复习迎考试卷数学试题Ⅱ(附加题)21.【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.A.选修4—1 几何证明选讲如图,AB是⊙O的直径,C、F为⊙O上的点,且CA平分∠BAF,过点C作CD⊥AF交AF的延长线于点D.求证:DC是⊙O的切线.【证明】连结OC,所以∠OAC=∠OCA.又因为CA平分∠BAF,所以∠OAC=∠FAC,于是∠FAC=∠OCA,所以OC//AD.又因为CD⊥AF,所以CD⊥OC,故DC是⊙O的切线.…………………10分B.选修4—2 矩阵与变换变换T是绕坐标原点逆时针旋转π2的旋转变换,求曲线22221xxyy在变换T作用下所得的曲线方程.【解】变换T所对应变换矩阵为0110M,设xy是变换后图像上任一点,与之对应的变换前的点是00xy,则00xxyyM,即00,,yxxy,代入220000221xxyy,即22221xxyy,所以变换后的曲线方程为22221xxyy.…………………10分C.选修4—4 参数方程与极坐标(本题满分10分)已知圆1O和圆2O的极坐标方程分别为2,2π22cos()24.(1)把圆1O和圆2O的极坐标方程化为直角坐标方程;(2)求经两圆交点的直线的极坐标方程.PCADBO·【解】(1)224,所以224xy;因为2π22cos24,所以2ππ22coscossinsin244,所以222220xyxy.………5分(2)将两圆的直角坐标方程相减,得经两圆交点的直线方程为1xy.化为极坐标方程为cossin1,即2πsin42.…………………10分D.选修4—5 不等式证明选讲(本题满分10分)已知0mabR,,,求证:22211ambambmm.【解】因为0m,所以10m,所以要证22211ambambmm,即证222()(1)()ambmamb,即证22(2)0maabb,即证2()0ab,而2()0ab显然成立,故22211ambambmm.……………10分江苏省高淳高级中学2011届高三上学期第二次质量检测(数学理)附加题21.本大题包括A,B,C,D共4小题,请从这4题中选做2小题.每小题10分,共20分.请在答题卡上准确填涂题目标记.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲如图,PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.求证:DPBDCP.【证明】因为PA与圆相切于A,所以2DADBDC,………………………2分因为D为PA中点,所以DP=DA,所以DP2=DB·DC,即PDDBDCPD.……………………5分因为BDPPDC,所以BDP∽PDC…………8分所以DPBDCP.…………………10分B.选修4—2:矩阵与变换曲线22421xxyy在二阶矩阵11aMb的作用下变换为曲线2221xy,求实数,ab的值;解:设(,)Pxy为曲线2221xy上任意一点,\'\'\'(,)Pxy为曲线22421xxyy上与P对应的点,则\'\'11axxbyy,即\'\'\'\'xxayybxy……………………6分代入的\'\'2\'\'2()2()1xaybxy得2222122421bxabxyay,及方程22421xxyy,从而2212124422baba,解得2,0ab,…………………10分C.选修4—4 参数方程与极坐标圆1O和圆2O的极坐标方程分别为4cossin,.(1)把圆1O和圆2O的极坐标方程化为直角坐标方程;(2)求经重1O,圆2O两个交点的直线的直角坐标方程.解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)cosx,siny,由4cos得24cos.所以224xyx.即2240xyx为圆1O的直角坐标方程.……………………………………3分同理220xyy为圆2O的直角坐标方程.……………………………………6分(2)由2222400xyxxyy 相减得过交点的直线的直角坐标方程为40xy.…………………………10分D.选修4—5:不等式选讲已知实数,0mn.(Ⅰ)求证:222()ababmnmn≥;(Ⅱ)求函数291((0,))122yxxx的最小值.答:(Ⅰ)证明:因为,0mn,利用柯西不等式,得222()()()abmnabmn≥,所以222()ababmnmn≥.………………………………………………5分(Ⅱ)由(Ⅰ),函数2222923(23)25122122(12)yxxxxxx≥,所以函数291((0,))122yxxx的最小值为25,当且仅当15x时取得.……10分展开内容







 20以内数字加减法练习(word版)
20以内数字加减法练习(word版)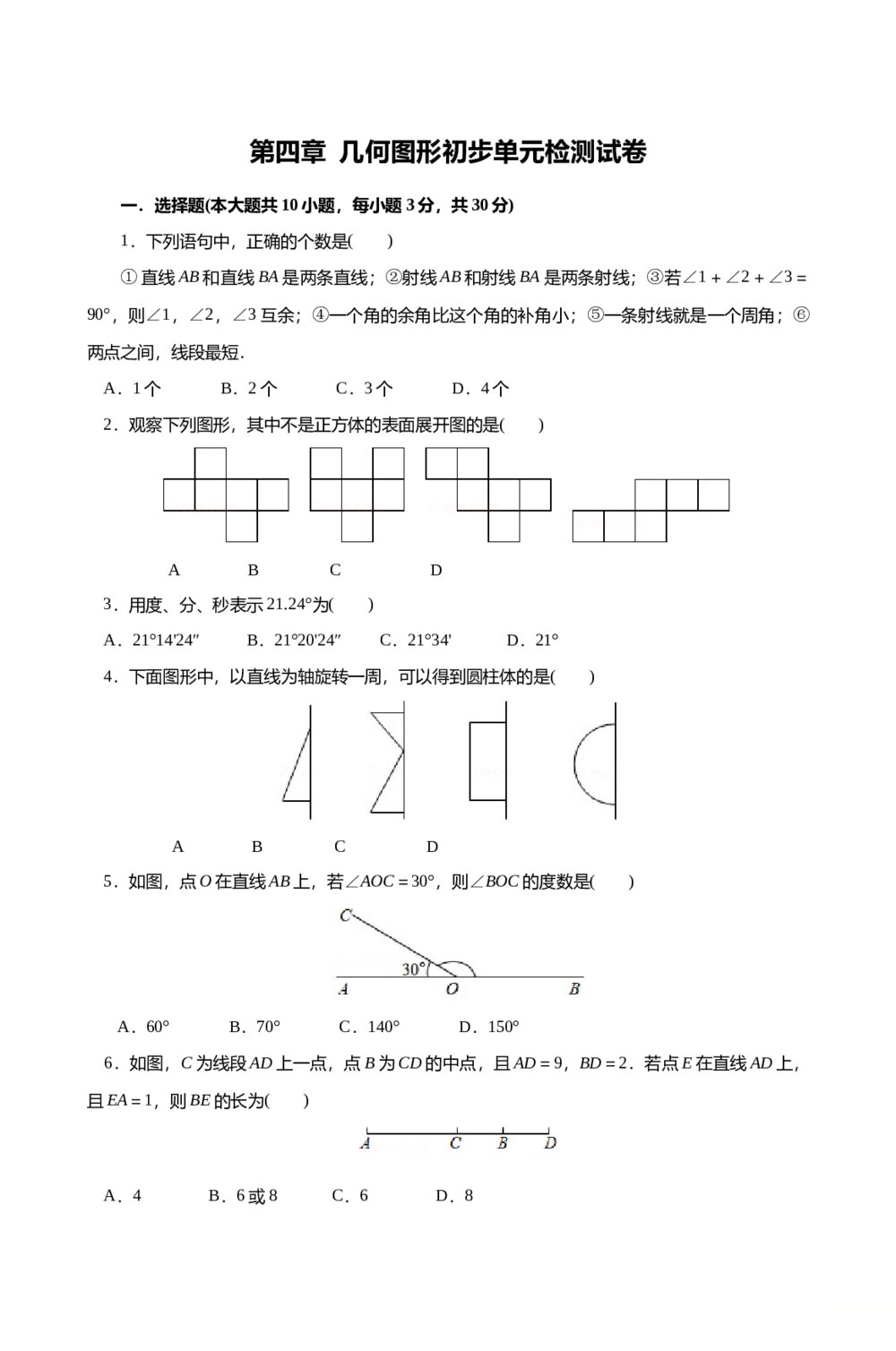 人教版七年级数学上册《第四章·几何图形初步单元检测试卷》+(含参考答案)
人教版七年级数学上册《第四章·几何图形初步单元检测试卷》+(含参考答案) 北京市石景山区高三一模数学文科+参考答案
北京市石景山区高三一模数学文科+参考答案 2011年全国统一高考数学试卷(理科)(大纲版)+(答案解析)
2011年全国统一高考数学试卷(理科)(大纲版)+(答案解析) 重庆卷2011全国高考(理科)数学试卷
重庆卷2011全国高考(理科)数学试卷 小学二年级数学应用题专项训练word
小学二年级数学应用题专项训练word