









试读已结束,还剩1页未读,您可下载完整版后进行离线阅读
《2012北京市东城区高三一模试卷数学(理科)+答案》是由用户上传到老师板报网,本为文库资料,大小为585.5 KB,总共有11页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 11页
- 585.5 KB
- VIP模板
- doc
- 数字产品不支持退货
北京市东城区2011-2012学年度第二学期高三综合练习(一)数学(理科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。考试时长120分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考试结束后,将本试卷和答题卡一并交回。第Ⅰ卷(选择题共40分)一、本大题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。(1)若a,bR,i是虚数单位,且(2)i1iab,则ab的值为(A)1(B)2(C)3(D)4(2)若集合},0{2mA,}2,1{B,则“1m”是“}2,1,0{BA”的(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件(3)若实数x,y满足不等式组1,2,0,yxyxy则yxz2的最小值为(A)27(B)2(C)1(D)25(4)右图给出的是计算1001...81614121的一个程序框图,其中判断框内应填入的条件是(A)50i(B)50i(C)25i(D)25i(5)某小区有排成一排的7个车位,现有3辆不同型号的车需要停放,如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为(A)16(B)18(C)24(D)32(6)已知x,y,zR,若1,x,y,z,3成等比数列,则xyz的值为C(A)3(B)3(C)33(D)33(7)在直角梯形ABCD中,已知BC∥AD,ABAD,4AB,2BC,4AD,若P为CD的中点,则PAPB的值为(A)5(B)4(C)4(D)5(8)已知函数21,0,()(1),0.xxfxfxx若方程()fxxa有且只有两个不相等的实数根,则实数a844647m9354551079乙甲BCDAOEDC1Q0N1CB1ABMQ的取值范围是(A),1(B),1(C)0,1(D)0,第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。(9)命题“000(0,),tansin2xxx”的否定是.(10)在极坐标系中,圆2的圆心到直线cossin2的距离为.(11)在如图所示的茎叶图中,乙组数据的中位数是;若从甲、乙两组数据中分别去掉一个最大数和一个最小数后,两组数据的平均数中较大的一组是组.(12)如图,AB是⊙O的直径,直线DE切⊙O于点D,且与AB延长线交于点C,若CD3,1CB,则ADE=.(13)抛物线2yx的准线方程为;经过此抛物线的焦点是和点(1,1)M,且与准线相切的圆共有个.(14)如图,在边长为3的正方形ABCD中,点M在AD上,正方形ABCD以AD为轴逆时针旋转角)3(0≤≤到11ABCD的位置,同时点M沿着AD从点A运动到点D,11MNDC,点Q在1MN上,在运动过程中点Q始终满足QM1cos,记点Q在面ABCD上的射影为0Q,则在运动过程中向量0BQ与BM夹角的正切的最大值为.三、解答题:本大题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。(15)(本小题共13分)PFEABCFA1CPBE已知函数22()(sin2cos2)2sin2fxxxx.(Ⅰ)求()fx的最小正周期;(Ⅱ)若函数()ygx的图象是由()yfx的图象向右平移8个单位长度,再向上平移1个单位长度得到的,当x[0,4]时,求()ygx的最大值和最小值.(16)(本小题共13分)某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%.生产1件甲产品,若是一等品,则获利4万元,若是二等品,则亏损1万元;生产1件乙产品,若是一等品,则获利6万元,若是二等品,则亏损2万元.两种产品生产的质量相互独立.(Ⅰ)设生产1件甲产品和1件乙产品可获得的总利润为X(单位:万元),求X的分布列;(Ⅱ)求生产4件甲产品所获得的利润不少于10万元的概率.(17)(本小题共13分)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足1AEFCCP.将△AEF沿EF折起到△1AEF的位置,使二面角1AEFB成直二面角,连结1AB,1AP.(如图2)(Ⅰ)求证:EA1⊥平面BEP;(Ⅱ)求直线EA1与平面BPA1所成角的大小.图1图2(18)(本小题共14分)已知函数221()2e3eln2fxxxxb在0(,0)x处的切线斜率为零.(Ⅰ)求0x和b的值;(Ⅱ)求证:在定义域内()0fx≥恒成立;(Ⅲ)若函数()()aFxfxx有最小值m,且2em,求实数a的取值范围.(19)(本小题共13分)已知椭圆C:222210xyabab的离心率是12,其左、右顶点分别为1A,2A,B为短轴的端点,△12ABA的面积为23.(Ⅰ)求椭圆C的方程;(Ⅱ)2F为椭圆C的右焦点,若点P是椭圆C上异于1A,2A的任意一点,直线1AP,2AP与直线4x分别交于M,N两点,证明:以MN为直径的圆与直线2PF相切于点2F.(20)(本小题共14分)若对于正整数k,()gk表示k的最大奇数因数,例如(3)3g,(10)5g.设(1)(2)(3)(4)(2)nnSggggg.(Ⅰ)求(6)g,(20)g的值;(Ⅱ)求1S,2S,3S的值;(Ⅲ)求数列nS的通项公式.北京市东城区2011-2012学年度第二学期高三综合练习(一)数学参考答案及评分标准(理科)一、选择题(本大题共8小题,每小题5分,共40分)(1)D(2)A(3)A(4)B(5)C(6)C(7)D(8)A二、填空题(本大题共6小题,每小题5分,共30分)(9)(0,),tansin2xxx(10)2(11)84乙(12)60(13)14x2(14)612注:两个空的填空题第一个空填对得2分,第二个空填对得3分.三、解答题(本大题共6小题,共80分)(15)(共13分)解:(Ⅰ)因为22()(sin2cos2)2sin2fxxxxsin4cos4xx2sin(4)4x,…………6分所以函数()fx的最小正周期为2.…………8分(Ⅱ)依题意,()ygx2sin[4()8x4]12sin(4)14x.…………10分因为04x,所以34444x.…………11分当442x,即316x时,()gx取最大值21;当444x,即0x时,()gx取最小值0.…………13分(16)(共13分)解:(Ⅰ)由题设知,X的可能取值为10,5,2,3.…………2分(10)PX0.80.90.72,(5)0.20.90.18PX,(2)0.80.10.08PX,(3)0.20.10.02PX.…………6分由此得X的分布列为:X10523P0.720.180.080.02…………8分(Ⅱ)设生产的4件甲产品中一等品有n件,则二等品有4n件.DPFEACBxyzA1FCPBE由题设知4(4)10nn,解得145n,又nN且4n,得3n,或4n.…………10分所求概率为33440.80.20.80.8192PC.(或写成512625)答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192.…………13分(17)(共13分)(Ⅰ)证明:取BE中点D,连结DF.因为1AECF,1DE,所以2AFAD,而60A,即△ADF是正三角形.又因为1AEED,所以EFAD.…………2分所以在图2中有1AEEF,BEEF.…………3分所以1AEB为二面角1AEFB的平面角.图1又二面角1AEFB为直二面角, 所以1AEBE.…………5分又因为BEEFE, 所以1AE⊥平面BEF,即1AE⊥平面BEP.…………6分(Ⅱ)解:由(Ⅰ)可知1AE⊥平面BEP,BEEF,如图,以E为原点,建立空间直角坐标系Exyz,则(0,0,0)E,1(0,0,1)A,(2,0,0)B,(0,3,0)F.在图1中,连结DP.因为12CFCPFAPB,所以PF∥BE,且12PFBEDE.所以四边形EFPD为平行四边形.所以EF∥DP,且EFDP.故点P的坐标为(1,3,0).图2所以1(2,0,1)AB,(1,3,0)BP,1(0,0,1)EA.…………8分不妨设平面1ABP的法向量(,,)xyzn,则10,0.ABBPnn即20,30.xzxy令3y,得(3,3,6)n. …………10分所以cos1EAn,11632||||143EAEAnn.…………12分故直线1AE与平面1ABP所成角的大小为3.…………13分(18)(共14分)(Ⅰ)解:23e()2efxxx.…………2分由题意有0()0fx即2003e2e0xx,解得0ex或03ex(舍去).…………4分得(e)0f即2221e2e3elne02b,解得21e2b.…………5分(Ⅱ)证明:由(Ⅰ)知2221e()2e3eln(0)22fxxxxx,()fx23e(e)(3e)2e(0)xxxxxx.在区间(0,e)上,有()0fx;在区间(e,)上,有()0fx.故()fx在(0,e)单调递减,在(e,)单调递增,于是函数()fx在(0,)上的最小值是(e)0f.…………9分故当0x时,有()0fx≥恒成立.…………10分(Ⅲ)解:23e()()2eaaFxfxxxx(0)x.当23ea时,则223e()2e23e2eaFxxax,当且仅当23exa时等号成立,故()Fx的最小值223e2ema2e,符合题意;…………13分当23ea时,函数()2eFxx在区间(0,)上是增函数,不存在最小值,不合题意;当23ea时,函数23e()2eaFxxx在区间(0,)上是增函数,不存在最小值,不合题意.综上,实数a的取值范围是2(3e,).…………14分(19)(共13分)(Ⅰ)解:由已知2221,223,.caababc…………2分解得2a,3b.…………4分故所求椭圆方程为22143xy.…………5分(Ⅱ)证明:由(Ⅰ)知12,0A,22,0A,21,0F.设000,2Pxyx,则22003412xy.于是直线1AP方程为0022yyxx,令4x,得0062Myyx;所以(M4,0062yx),同理(N4,0022yx).…………7分所以2FM(3,0062yx),2FN(3,0022yx).所以22FMFN(3,0062yx)(3,0022yx)000062922yyxx220022003123129944xyxx20209499904xx.所以22FMFN,点2F在以MN为直径的圆上.…………9分设MN的中点为E,则(4,E00204(1)4yxx).…………10分又2FE(3,00204(1)4yxx),2001,,FPxy所以22FEFP(3,00204(1)4yxx)20000020411,314yxxyxx20000020123131313104xxxxxx.所以22FEFP.…………12分因为2FE是以MN为直径的圆的半径,E为圆心,22FEFP,故以MN为直径的圆与直线2PF相切于右焦点.…………13分(20)(共14分)解:(Ⅰ)(6)3g,(20)5g.…………2分(Ⅱ)1(1)(2)112Sgg;2(1)(2)(3)(4)11316Sgggg;3(1)(2)(3)(4)(5)(6)(7)(8)1131537122Sgggggggg.…………6分(Ⅲ)由(Ⅰ)(Ⅱ)不难发现对mN,有(2)()gmgm.…………8分所以当2n时,(1)(2)(3)(4)(21)(2)nnnSgggggg[(1)(3)(5)(21)][(2)(4)(2)]nnggggggg1[135(21)][(21)(22)(22)]nnggg11(121)2[(1)(2)(2)]2nnnggg114nnS…………11分于是114nnnSS,2,nnN.所以112211()()()nnnnnSSSSSSSS12244442nn14(14)4221433nn,2,nnN.…………13分又12S,满足上式,所以对nN,1(42)3nnS.…………14分展开内容










 2015高三数学《文科》二轮复习《专题4 立体几何》PPT版
2015高三数学《文科》二轮复习《专题4 立体几何》PPT版 九年级第一学期数学期末测评试卷+参考答案(word版)
九年级第一学期数学期末测评试卷+参考答案(word版) 2011年高考一轮课时训练(理)13.1事件与概率+参考答案(通用版)
2011年高考一轮课时训练(理)13.1事件与概率+参考答案(通用版) 青岛版六年级数学上册《归类培优测试卷3图形与几何和统计与概率》+答案
青岛版六年级数学上册《归类培优测试卷3图形与几何和统计与概率》+答案 2012高考(文科)数学试卷+答案(新课标全国卷)
2012高考(文科)数学试卷+答案(新课标全国卷)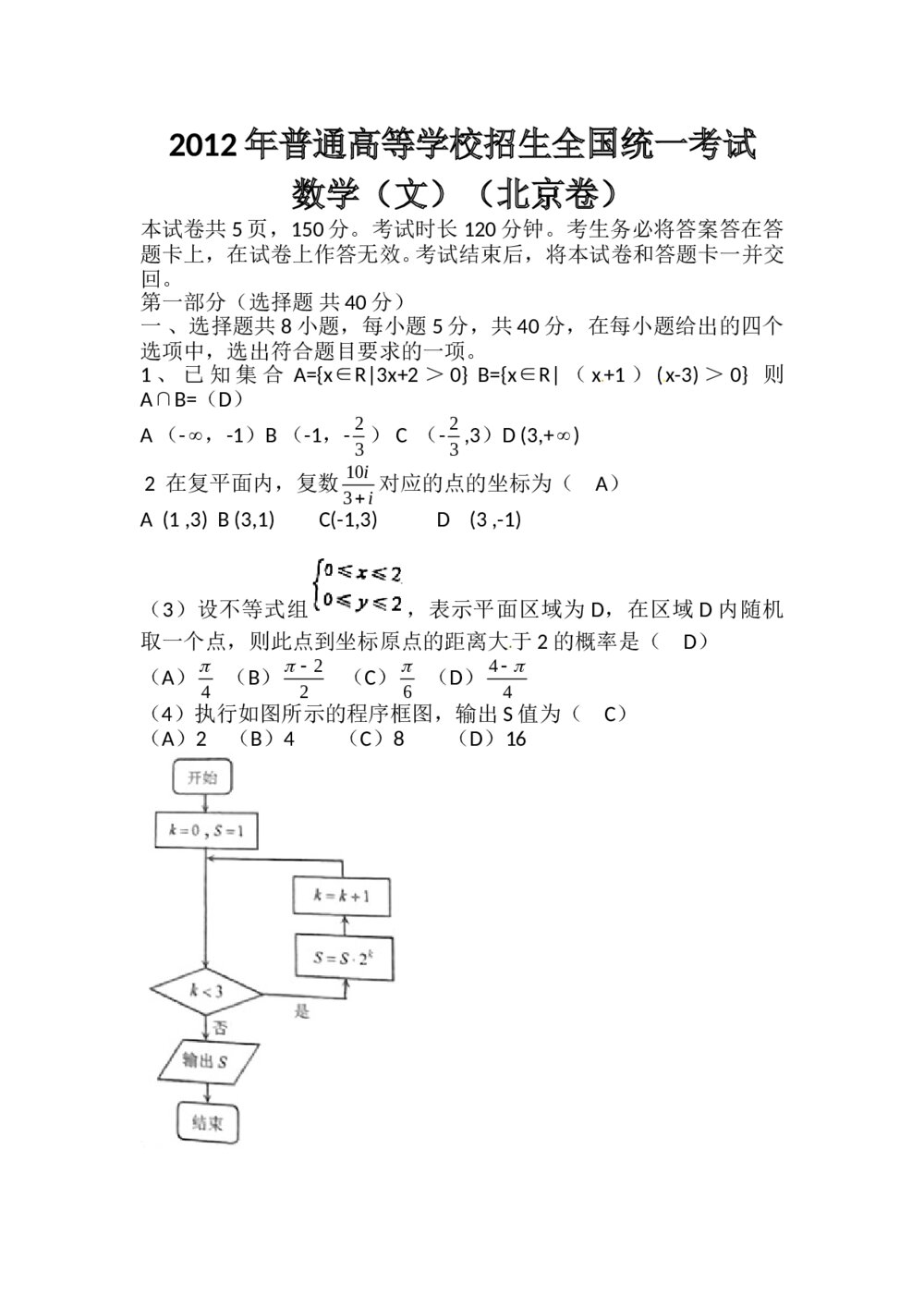 2012北京卷高考数学(文科)试题+答案
2012北京卷高考数学(文科)试题+答案