









试读已结束,还剩118页未读,您可下载完整版后进行离线阅读
《2015高三数学《文科》二轮复习《专题4 立体几何》PPT版》是由用户上传到老师板报网,本为文库资料,大小为20.36 MB,总共有128页,格式为ppt。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 128页
- 20.36 MB
- VIP模板
- ppt
- 数字产品不支持退货
第10讲 空间几何体的三视图﹑表面积与体积 第11讲空间中的平行与垂直第12讲空间角专题四 立体几何专题四 立体几何第第1010讲 空间几何体的三讲 空间几何体的三视图视图﹑﹑表面积与体积表面积与体积返回目录考点考向探究核心知识聚焦第10讲 空间几何体的三视图﹑表面积与体积体验高考体验高考1.[2013·四川卷改编]一个几何体的三视图①如图101所示,则该几何体可以是________.⇒直观图与三视图关键词:直观图、三视图如①、正视图、侧视图、俯视图.主干知识主干知识图101核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析]正视图和侧视图均为等腰梯形,俯视图为两个同心圆,只有圆台的三视图符合此要求.[答案]圆台核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积体验高考体验高考 2.[2013·重庆卷改编]某几何体的三视图如图102所示,则该几何体的表面积②为________.⇒表面积关键词:棱柱(锥、台)、圆柱(锥、台)、球的表面积公式,几何体的表面积如②.主干知识主干知识图102核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析]该几何体为直四棱柱,其高为10,底面是上底为2,下底为8,高为4,其腰为5的等腰梯形,所以底面面积和为12(2+8)×4×2=40.四个侧面的面积和为(2+8+5×2)×10=200,所以该直四棱柱的表面积S=40+200=240.[答案]240核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积体验高考体验高考 3.[2014·天津卷]一个几何体的三视图如图103所示(单位:m),则该几何体的体积③为________m3.⇒体积关键词:球、棱柱(锥、台)、圆柱(锥、台)的体积公式,几何体的体积如③④.主干知识主干知识 图103核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析]由三视图可得,该几何体为圆柱与圆锥的组合体,其体积V=π×12×4+13π×22×2=20π3.[答案]20π3核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积体验高考体验高考 4.[2014·新课标全国卷Ⅱ改编]正三棱柱ABCA1B1C1的底面边长为2,侧棱长为3,D为BC中点,则三棱锥AB1DC1的体积④为________.[答案]1[解析]因为D为BC的中点,所以AD⊥BC,故AD⊥平面BCC1B1,且AD=3,所以11ABDCV三棱锥=1311BDCSV·AD=13×12B1C1·BB1·AD=13×12×2×3×3=1.核心知识聚焦返回目录第10讲 空间几何体的三视图﹑表面积与体积体验高考体验高考 5.[2013·天津卷]已知一个正方体的所有顶点在一个球面上⑤,若球的体积为9π2,则正方体的棱长为________.⇒球与几何体关键词:球内接多面体如⑤,球外切多面体.主干知识主干知识 [答案]3[解析]设正方体的棱长为a,则43π3a23=92π,解之得a=3.核心知识聚焦返回目录正视图光线从几何体的前面向后面正投影,得到的投影图侧视图光线从几何体的左面向右面正投影,得到的投影图三视图俯视图光线从几何体的上面向下面正投影,得到的投影图正视图与侧视图高平齐;侧视图与俯视图宽相等;俯视图与正视图长对正画法使用斜二测画法画出空间几何体的底,再画出空间几何体的其他部分空间几何体直观图面积关系水平放置的平面图形的面积为S,使用斜二测画法画出的直观图的面积为S′,则S=22S′第10讲 空间几何体的三视图﹑表面积与体积————教师教师知识必备知识必备———— 知识必备空间几何体返回目录表面积体积棱柱S表=S侧+2S底V=S底·h高棱锥S表=S侧+S底V=13S底·h高棱台S表=S侧+S上底+S下底V=13(S′+S′S+S)h圆柱S表=2πr2+2πrhV=πr2h圆锥S表=πr2+πrlV=13πr2h圆台S表=π(r′2+r2+r′l+rl)V=13π(r′2+r′r+r2)h空间几何体表面积和体积球S球=4πR2表面积即空间几何体暴露在外的所有面的面积之和V球=43πR3第10讲 空间几何体的三视图﹑表面积与体积————教师教师知识必备知识必备———— 返回目录第10讲 空间几何体的三视图﹑表面积与体积►考点一三视图与直观图几何体——1.各种几何体的概念;2.几何体的结构三视图——1.作三视图;2.判断三视图;3.根据三视图判断直观图直观图——1.根据直观图计算与证明;2.根据直观图得三视图题型:选择,填空分值:5分难度:基础热点:三视图考点考向探究返回目录返回目录第10讲 空间几何体的三视图﹑表面积与体积例1[2014·新课标全国卷Ⅰ]如图104所示,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱图104考点考向探究第10讲 空间几何体的三视图﹑表面积与体积(2)[2014·新课标全国卷Ⅱ]如图105所示,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.1727B.59C.1027D.13考点考向探究图105考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析](1)从俯视图为矩形可以看出,此几何体不可能是三棱锥和四棱,其直观图如图所示,是一个三棱柱.(2)该零件是一个由两个圆柱组成的组合体,其体积V=π×32×2+π×22×4=34π(cm3),原毛坯的体积V毛坯=π×32×6=54π(cm3),被切部分的体积V切=V毛坯-V=54π-34π=20π(cm3),所以V切V毛坯=20π54π=1027.[答案](1)B(2)C考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积[小结]根据所给的三视图确定几何体的表面积和体积,一般要经过以下步骤:①确定几何体的组成,即是拼接、切掉,还是挖掉等;②组成的简单几何体的名称,即是棱柱、棱锥,还是圆锥、球等;③每个简单几何体的具体数据;④依据相关公式计算.考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积变式题(1)某几何体的正视图和侧视图完全相同,均如图106所示,则该几何体的俯视图一定不可能是()图106图107(2)一个几何体的三视图如图108所示,则该几何体的表面积为__________.图108考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析](1)由正视图和侧视图知,该几何体为组合体,上部分可能是圆柱,也可能是棱柱,但是如果俯视图为D时,那么正视图上半部分中间应有一条虚线,所以不可能是D.(2)由三视图可知,该几何体是一个上部分为半球,下部分为长方体的简单组合体,故该几何体的表面积为12×4π×22+π×22+4×2×3=12π+24.[答案](1)D(2)12π+24考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积►考点二几何体的表面积与体积表面积——1.几何体的表面积计算公式;2.求几何体的表面积体积——1.几何体的体积计算公式;2.求几何体的体积题型:选择,填空,解答分值:5-6分难度:中等热点:几何体的表面积与体积考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积例2(1)[2014·山东卷]一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为__________.(2)已知正方体ABCDA1B1C1D1的棱长为2,线段EF,GH分别在AB,CC1上移动,且EF+GH=12,则四面体EFGH的体积的最大值为__________.[答案](1)12(2)148考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积[解析](1)设该六棱锥的高是h.根据体积公式得,V=13×12×2×3×6×h=23,解得h=1,则侧面三角形的高为1+(3)2=2,所以侧面积S=12×2×2×6=12.(2)如图所示,连接EC,FC,设EF=x,CG=y则GH=12-x,考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积即当EF=GH=14时,四面体EFGH的体积最大,最大值为148.V三棱锥HEFG=V三棱锥HEFC-V三棱锥GEFC=13×12x×2×12-x+y-13×12×2xy=13x12-x=-13x-142+148≤148,考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积考点考向探究[小结]求规则几何体的体积,只需确定底面与相应的高,而一些不规则几何体的体积往往需采用分割或补形思想,转化求解.考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积变式题(1)某四面体的三视图均为直角三角形,如图109所示,则该四面体的表面积为()A.72+242B.96+242C.126D.64(2)三棱锥PABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥PABC的体积等于________.图109考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积[解析](1)根据三视图可知,该几何体的直观图如图所示,其中SA⊥平面ABC,AB⊥BC,且有AB=SA=8,BC=6,所以AC=10,SB=82,所以该四面体的表面积S=12×8×8+12×6×82+12×8×10+12×8×6=96+242.(2)由已知,得S△ABC=12×22×sinπ3=3,∴V三棱锥PABC=13S△ABC·PA=13×3×3=3,即三棱锥PABC的体积等于3.[答案](1)B(2)3考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积►考点三多面体与球多面体与球——1.多面体与球的位置关系;2.球的有关计算题型:选择,填空,解答分值:5-10分难度:中等热点:有关球的表面积与体积的计算考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积例3[2014·湖南卷]一块石材表示的几何体的三视图如图1010所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4图1010[解析]由三视图可知,石材为一个三棱柱(相对应的长方体的一半),故可知能得到的最大球为三棱柱的内切球,由题意知,正视图中三角形的内切圆的半径即为球的半径,可得R=6+8-102=2.[答案]B考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积[小结]球与多面体主要考查多面体的外接球和多面体的内切球两种.一般先要确定球心的位置,再分析球的半径与多面体棱长之间的数量关系,有时还需要将多面体进行补形,如补成长方体等.考点考向探究返回目录 第10讲 空间几何体的三视图﹑表面积与体积变式题球面上有四个点P,A,B,C,若PA,PB,PC两两互相垂直,且PA=PB=PC=1,则该球的表面积是________.[解析]∵PA,PB,PC两两互相垂直,且PA=PB=PC=1,∴分别以PA,PB,PC为棱作一个正方体.设所得正方体的外接球为球O,则P,A,B,C四点所在的球面就是球O表面,易知正方体的体对角线的长度等于球O的直径,即2R=PA2+PB2+PC2=3,∴R=32,∴球O的表面积S=4πR2=4π322=3π.[答案]3π考点考向探究返回目录第10讲 空间几何体的三视图﹑表面积与体积例1[配例1使用]一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()————教师备用例题教师备用例题———— [备选理由]例1既考查对三视图的认识、鉴别,又涉及空间点的坐标的确定;例2将几何体体积的计算与几何概型结合起来考查,有一定的综合性;例3为圆锥与球这两个旋转体之间的位置关系与体积的计算.返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析]四面体OABC如图所示,点B,C在zOx平面内的正投影的坐标分别是M(1,0,0),N(0,0,1),线段AB,BC,AC,OB,OC在zOx面上的正投影分别是实线段AM,MN,AN,OM,ON,遮挡住的线段OA的投影使用虚线,故其正视图为选项A中的图形.[答案]A返回目录第10讲 空间几何体的三视图﹑表面积与体积例2[配例2使用]如图所示,在长方体ABCDA1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCDA1B1C1D1内随机选取一点,则该点取自于几何体A1ABFED1DCGH内的概率为________.返回目录第10讲 空间几何体的三视图﹑表面积与体积[解析]设三棱柱EFB1HGC1的体积为V1,长方体ABCDA1B1C1D1的体积为V.因为EH∥A1D1,则EH∥B1C1,所以EH∥平面BCC1B1.过EH的平面与平面BCC1B1交于FG,则EH∥FG,所以易证明几何体A1ABFED1DCGH和EB1FHC1G是等高的五棱柱和三棱柱,由几何概型可知,所求概率P=1-V1V=1-111EBFABBASSV矩形=1-12×55a×255a2a2=910.[答案]910返回目录第10讲 空间几何体的三视图﹑表面积与体积例3[配例3使用]若圆锥的内切球与外接球的球心重合,且内切球的半径为1,则圆锥的体积为________.[解析]过圆锥的旋转轴作轴截面,得△ABC及其内切圆⊙O1和外接圆⊙O2,且两圆为同心圆,即△ABC的内心与外心重合,易得△ABC为正三角形.由题意知,⊙O1的半径r=1,∴△ABC的边长为23,∴圆锥的底面半径为3,高为3,∴圆锥的体积V=13×π×3×3=3π.[答案]3π返回目录第第1111讲 空间中的平行与垂直讲 空间中的平行与垂直考点考向探究核心知识聚焦返回目录第11讲 空间中的平行与垂直体验高考体验高考1.[2014·辽宁卷改编]已知m,n表示两条不同直线,α表示平面,若m⊥α,n⊂α,则m与n的位置关系①为________.[答案]垂直[解析]根据线面垂直的定义知,若m⊥α,则m垂直于平面α内任一直线,所以m⊥n.⇒点线面位置关系关键词:点与线、线与线如①、线与面、面与面的关系.主干知识主干知识核心知识聚焦返回目录第11讲 空间中的平行与垂直体验高考体验高考 2.[2013·全国课标卷Ⅱ改编]如图111所示,直三棱柱ABCA1B1C1中,D是AB的中点.则BC1与平面A1CD的位置关系②是________.图111⇒平行关系关键词:线线平行、线面平行如②、面面平行、平行的判断与性质.主干知识主干知识核心知识聚焦返回目录第11讲 空间中的平行与垂直[解析]连接AC1交A1C于点F,连接DF,D,F分别为AB,AC1的中点,则BC1∥DF,DF⊂平面A1CD,所以BC1∥平面A1CD.[答案]平行核心知识聚焦返回目录第11讲 空间中的平行与垂直体验高考体验高考 3.[2014·江西卷改编]如图112所示,三棱柱ABCA1B1C1中,AA1⊥BC,A1B⊥BB1,则A1C与CC1的位置关系③是________.图112⇒垂直关系关键词:线线垂直如③、线面垂直如④⑤、面面垂直、垂直的判断与性质.主干知识主干知识核心知识聚焦返回目录第11讲 空间中的平行与垂直[解析]由AA1⊥BC知,BB1⊥BC又BB1⊥A1B,故BB1⊥平面BCA1,所以BB1⊥A1C.又BB1∥CC1,所以A1C⊥CC1.[答案]垂直核心知识聚焦返回目录第11讲 空间中的平行与垂直体验高考体验高考 核心知识聚焦4.[2014·福建卷改编]如图113所示,三棱锥ABCD中,AB⊥平面BCD,CD⊥BD,则CD与平面ABD的位置关系④是________.图113[解析]∵AB⊥平面BCD,CD⊂平面BCD,∴AB⊥CD.又∵CD⊥BD,AB∩BD=B,AB⊂平面ABD,BD⊂平面ABD,∴CD⊥平面ABD.[答案]垂直核心知识聚焦返回目录第11讲 空间中的平行与垂直体验高考体验高考 5.[2014·浙江卷改编]设m,n是两条不同的直线,α,β是两个不同的平面,若m⊥β,n⊥β,n⊥α,则直线m与平面α的位置关系⑤是________.[解析]若m⊥β,n⊥β,则m∥n,而n⊥α,所以m⊥α.[答案]m⊥α核心知识聚焦返回目录第11讲 空间中的平行与垂直————教师教师知识必备知识必备———— 知识必备空间点、直线、平面的位置关系公理1A∈l,B∈l,且A∈α,B∈α⇒l⊂α判断直线在平面内公理2A,B,C不共线⇒A,B,C确定一个平面确定平面公理3P∈α,且P∈β⇒α∩β=l,且P∈l确定两平面的交线基本公理公理4a∥c,b∥c⇒a∥b用途两直线平行线线共面和异面:共面为相交或平行,不同在任何一个平面内的两条直线称为异面直线点线面A∈l,B∉l;A∈α,B∉α线面l∥α,l∩α=A,l⊂α分别对应线面无公共点、线面有一个公共点和线面有无数个公共点空间点、直线、平面的位置关系位置关系面面α∥β,α∩β=l分别对应两平面无公共点、两平面有无数个公共点返回目录判定定理性质定理线面a⊄α,b⊂α,a∥b⇒a∥α线线平行⇒线面平行a∥α,a⊂β,α∩β=b⇒a∥b线面平行⇒线线平行平行关系面面,ababPabIβ,β∥,∥⇒β∥α线面平行⇒面面平行α∥β,γ∩α=a,γ∩β=b⇒a∥b面面平行⇒线线平行线面,,,mnmnpamanI⇒a⊥α线线垂直⇒线面垂直ab⇒a∥b线面垂直⇒线线平行空间点、直线、平面的位置关系垂直关系面面l⊥β,l⊂α⇒α⊥β线面垂直⇒面面垂直α⊥β,α∩β=l,a⊂α,a⊥l⇒aβ⊥面面垂直⇒线面垂直第11讲 空间中的平行与垂直————教师教师知识必备知识必备———— 返回目录第11讲 空间中的平行与垂直————教师教师知识必备知识必备———— 点面距从平面外一点作平面的垂线,该点与垂足之间的距离线面距直线与平面平行时,直线上任一点到平面的距离空间点、直线、平面的位置关系空间距离面面距两个平面平行时,一个平面内任一点到另一个平面的距离线面距和面面距可转化为点面距返回目录第11讲 空间中的平行与垂直►考点一点、线、面间位置关系的判断位置关系——1.判定点在平面内;2.判定两直线异面;3.平行问题的判定;4.垂直问题的判定题型:选择,填空,解答分值:5分难度:中等热点:异面、平行与垂直考点考向探究返回目录第11讲 空间中的平行与垂直例1(1)设m,n是两条不同的直线,α,β是两个不同的平面,下列说法正确的是()A.若m∥α,n∥β且α∥β,则m∥nB.若m⊥α,n⊥β且α⊥β,则m⊥nC.若m⊥α,n⊂β,m⊥n,则α⊥βD.若m⊂α,n⊂α,m∥β,n∥β,则α∥β(2)下列命题为真命题的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行考点考向探究返回目录第11讲 空间中的平行与垂直[解析](1)直线m,n也可能异面或相交,故选项A中的说法不正确;m⊥α,α⊥βm∥β或mβ,又n⊥β,所以m⊥n,故选项B中的说法正确;当α∥β时,也符合已知条件,故选项C中的说法不正确;如果m∥n,则α,β也可能相交,故选项D中的说法不正确.考点考向探究[答案](1)B(2)C返回目录第11讲 空间中的平行与垂直(2)如图所示,在正方体ABCDA1B1C1D1中,直线D1A和D1C与底面ABCD所成的角均为45°,但是直线D1A和D1C相交,所以A选项错误;取AA1,BB1,CC1,DD1的中点A2,B2,C2,D2,连接A2B2,B2C2,C2D2,A2D2,则A,C,D1三点到平面A2B2C2D2的距离相等,但是平面ACD1与平面A2B2C2D2相交,所以B选项错误;易知BB1∥平面AA1D1D,BB1∥平面CC1D1D,且直线BB1与平面AA1D1D和平面CC1D1D的交线DD1平行,所以C选项正确;平面AA1D1D和平面CC1D1D都与平面ABCD垂直,但是平面AA1D1D和平面CC1D1D相交,所以D选项错误.故选C.考点考向探究返回目录第11讲 空间中的平行与垂直[小结]空间点、线、面位置关系的分析判断的依据是四个公理、平行关系与垂直关系的判定定理和性质定理,处理具体问题时可以构建长方体或三棱锥等模型,把要考查的点、线、面融入模型中,判断会简捷明了.考点考向探究返回目录 第11讲 空间中的平行与垂直变式题(1)已知直线a,b异面,给出以下命题:①一定存在平行于a的平面α,使得b⊥α;②一定存在平行于a的平面α,使得b∥α;③一定存在平行于a的平面α,使得b⊂α;④一定存在无数个平行于a的平面α与b交于一定点.其中真命题的序号是()A.①④B.②③C.①②③D.②③④(2)已知E,F,G,H是空间四点,条件甲:E,F,G,H四点不共面,条件乙:直线EF和GH不相交,则甲是乙成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件考点考向探究返回目录 第11讲 空间中的平行与垂直[解析](1)若b⊥α,且a∥α,则b⊥a,但a,b仅异面,所以①错;在直线a上任选一点O,过O作直线b′∥b,再过a,b′作平面β,则b∥β,所以只要作α∥β(不过b),就一定有b∥α,所以②正确;根据前面的分析,同理也知③正确;若在b上任取一点O,则过O可作无数个平面与a平行,所以④正确.(2)易知当E,F,G,H四点不共面时,EF,GH一定不相交,故甲可以推出乙;反之,若EF,GH不相交,则EF与GH有平行和异面两种情况,当EF与GH平行时,E,F,G,H四点共面,故乙不能推出甲.所以甲是乙的充分不必要条件.[答案](1)D(2)A考点考向探究返回目录第11讲 空间中的平行与垂直►考点二线、面平行关系平行关系——1.判定两直线平行;2.判定线面平行;3.判定面面平行;4.平行性质的应用题型:解答分值:5-6分难度:中等热点:判定平行关系考点考向探究返回目录第11讲 空间中的平行与垂直例2[2014·山东卷改编]如图114所示,四棱锥PABCD中,AP⊥平面PCD,AD∥BC,AB=BC=12AD,E,F分别为线段AD,PC的中点.求证:AP∥平面BEF.图114考点考向探究返回目录 第11讲 空间中的平行与垂直证明:设AC∩BE=O,连接OF,EC.由于E为AD的中点,AB=BC=12AD,AD∥BC,所以AE∥BC,AE=AB=BC,因此四边形ABCE为菱形,所以O为AC的中点.又在△PAC中,F为PC的中点,所以AP∥OF.又OF⊂平面BEF,AP⊄平面BEF.所以AP∥平面BEF.考点考向探究返回目录 第11讲 空间中的平行与垂直[小结]要证线面平行,主要有两个途径:一是证已知直线与平面内的某直线平行;二是证过已知直线的平面与已知平面平行.在这里转化思想在平行关系中起着重要的作用,即线线平行、线面平行、面面平行可以相互转化.在寻求平行关系时,利用中位线、平行四边形等知识是非常常见的手段.考点考向探究返回目录 第11讲 空间中的平行与垂直变式题如图115所示,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,FE=12AD,点G为AC的中点.求证:EG∥平面ABF.图115考点考向探究返回目录 第11讲 空间中的平行与垂直证明:取AB的中点M,连接FM,GM.∵G为对角线AC的中点,∴GM∥AD,且GM=12AD.又∵FE∥AD,且EF=12AD,∴GM∥FE,且GM=FE,∴四边形GMFE为平行四边形,即EG∥FM.又∵EG⊄平面ABF,FM⊂平面ABF,∴EG∥平面ABF.考点考向探究返回目录 第11讲 空间中的平行与垂直►考点三线、面垂直关系垂直关系——1.线线垂直的判定;2.线面垂直的判定;3.面面垂直的判定;4.垂直关系性质的应用题型:解答分值:5-6分难度:较难热点:垂直关系考点考向探究返回目录 第11讲 空间中的平行与垂直例3[2013·北京卷改编]如图116所示,在四棱锥PABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点,求证:(1)PA⊥平面ABCD;(2)平面BEF⊥平面PCD.图116考点考向探究返回目录第11讲 空间中的平行与垂直证明:(1)因为平面PAD⊥平面ABCD,且PA垂直于这两个平面的交线AD,所以PA⊥平面ABCD.(2)因为AB∥CD,CD=2AB,E为CD的中点,所以AB∥DE,且AB=DE,所以四边形ABED为平行四边形.又因为AB⊥AD,AB∥CD,所以BE⊥CD,AD⊥CD,由(1)知PA⊥底面ABCD,所以PA⊥CD.又因为PA∩AD=A,所以CD⊥平面PAD,所以CD⊥PD.因为E和F分别是CD和PC的中点,所以PD∥EF,所以CD⊥EF.又EF∩BE=E,所以CD⊥平面BEF,所以平面BEF⊥平面PCD.考点考向探究返回目录第11讲 空间中的平行与垂直[小结]在证明线线垂直时,要注意隐含的垂直关系,如等腰三角形的三线合一、矩形的相邻两边、直径所对的圆周角、菱形的两条对角线、经计算可得的直角三角形等.考点考向探究返回目录 第11讲 空间中的平行与垂直变式题如图117所示,在三棱柱ABCA1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,BA=2,BC=1,∠BCC1=π3.(1)求证:C1B⊥平面ABC;(2)试在棱CC1(不包含端点C,C1)上确定一点E,使得EA⊥EB1.图117考点考向探究返回目录 第11讲 空间中的平行与垂直考点考向探究解:(1)∵AB⊥侧面BB1C1C,∴AB⊥BC1.在△BC1C中,BC=1,CC1=BB1=2,∠BCC1=π3,由余弦定理有BC1=BC2+CC21-2·BC·CC1·cos∠BCC1=1+4-2×2×cosπ3=3,故有BC2+BC21=CC21,∴C1B⊥BC.又BC∩AB=B,且AB,BC⊂平面ABC.∴C1B⊥平面ABC.考点考向探究返回目录 第11讲 空间中的平行与垂直(2)连接BE,由于EA⊥EB1,AB⊥EB1,AB∩AE=A,AB,AE⊂平面ABE.∴B1E⊥平面ABE,且BE⊂平面ABE,故BE⊥B1E.不妨设CE=x(0<x<2),则C1E=2-x.又∠B1C1C=23π,则BE2=1+x2-x,B1E2=x2-5x+7.在Rt△BEB1中,x2-5x+7+x2-x+1=4.从而x=1或x=2(舍去),故E为CC1的中点时,EA⊥EB1.考点考向探究返回目录 第11讲 空间中的平行与垂直►考点四图形的折叠问题折叠问题——平面图形折叠成立体题型:填空,解答分值:5-14分难度:中等热点:图形的折叠考点考向探究返回目录 第11讲 空间中的平行与垂直例4如图118所示,梯形ABCD中AD∥BC,∠ABC=90°,AD∶BC∶AB=2∶3∶4,E,F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:①DF⊥BC;②BD⊥FC;图11-8③平面DBF⊥平面BFC;④平面DCF⊥平面BFC.在翻折过程中,可能成立的结论是________.(填写结论的序号)考点考向探究返回目录 第11讲 空间中的平行与垂直[解析]考虑①,因为BC∥AD,AD与DF相交不垂直,所以BC与DF不垂直,则①不成立;考虑②,设点D的在平面BCF上的射影为点P,当BP⊥CF时就有BD⊥FC,而AD∶BC∶AB=2∶3∶4可使条件满足,所以②正确;考虑③,当P点落在BF上时,DP⊂平面BDF,从而平面BDF⊥平面BCF,所以③正确;考虑④,因为点D的射影不可能在FC上,所以④不成立.[答案]②③考点考向探究返回目录第11讲 空间中的平行与垂直[小结]平面图形折叠成立体图形时,一定要注意折叠前后基本元素的变化,特别要注意成直角的两直线有没有变化,这对立体几何中线面垂直的判断有决定性作用.考点考向探究返回目录 第11讲 空间中的平行与垂直变式题如图119(1)所示,四边形ABCD为矩形,PD⊥平面ABCD,AB=1,BC=PC=2,作如图119(2)所示的折叠,折痕EF∥DC,其中点E,F分别在线段PD,PC上,沿EF折叠后点P叠在线段AD上的点记为M,并且MF⊥CF.(1)证明:CF⊥平面MDF;(2)求三棱锥MCDE的体积.(1)(2)图119考点考向探究返回目录 第11讲 空间中的平行与垂直解:(1)证明:∵PD⊥平面ABCD,PD⊂平面PCD,∴平面PCD⊥平面ABCD.又平面PCD∩平面ABCD=CD,MD⊂平面ABCD,MD⊥CD,∴MD⊥平面PCD.又CF⊂平面PCD,∴CF⊥MD.又CF⊥MF,MD,MF⊂平面MDF,MD∩MF=M,∴CF⊥平面MDF.考点考向探究返回目录 第11讲 空间中的平行与垂直(2)∵CF⊥平面MDF,∴CF⊥DF.易知∠PCD=60°,∴∠CDF=30°,从而CF=12CD=12.∵EF∥DC,∴DEDP=CFCP,即DE3=122,∴DE=34,∴PE=334,∴S△CDE=12CD·DE=38,MD=ME2-DE2=PE2-DE2=3342-342=62,∴V三棱锥MCDE=13S△CDE·MD=13×38×62=216.考点考向探究返回目录第11讲 空间中的平行与垂直例1[配例1使用]空间中,若a,b,c为三条不同的直线,α,β,γ为三个不同的平面,则下列命题为真命题的是()A.若a∥α,b∥α,则a∥bB.若a∥α,a∥β,则α∥βC.若a⊥α,b⊥α,则a∥bD.若α⊥β,α⊥γ,则β∥γ————教师备用例题教师备用例题———— [备选理由]例1给出了一个有三线三面的比较复杂的线线、线面、面面位置关系的判断问题;例2为综合考查线面的交点问题;例3以考查线面位置为主,涉及三视图的认识及体积的计算等探究性问题;例4给出的是垂直关系的证明以及线面角的计算;例5考查位置关系及用等积法求棱锥的高.返回目录第11讲 空间中的平行与垂直[解析]如图所示,在正方体ABCDA1B1C1D1中,AB,BC都与上底面A1B1C1D1平行,但AB与BC相交,所以A错;AB平行于上底面A1B1C1D1,也平行侧面CC1D1D,但上底面A1B1C1D1与侧面CC1D1D不平行,所以B错;侧面BCC1B1垂直于底面ABCD,也垂直于侧面CC1D1D,但侧面CC1D1D与底面ABCD垂直,所以D错.故选C.[答案]C返回目录第11讲 空间中的平行与垂直例2[配例1使用][2013·江西卷改编]如图所示,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=________.[解析]直线CE与正方体的上底面平行,且在下底面内,与其他四个平面相交,直线EF与正方体的左右两个平面平行,与其他四个平面相交,所以m=4,n=4,则m+n=8.[答案]8返回目录第11讲 空间中的平行与垂直例3[配例2、例3使用]已知一个四棱锥的三视图和直观图如图所示,且俯视图中∠DAB=60°,直观图中E为侧棱PD的中点.(1)求证:PB∥平面AEC.(2)若F为侧棱PA上的一点,且PFFA=λ,则当λ为何值时,PA⊥平面BDF?并求此时几何体FBDC的体积.返回目录第11讲 空间中的平行与垂直解:(1)证明:由图可知,该四棱锥的底面ABCD是一个菱形,且∠DAB=60°,边长为2,锥体的高为1.设AC,BD的交点为O,连接OE,则OE为△DPB的中位线,∴OE∥PB.又EO⊂平面EAC,PB⊄平面EAC,∴PB∥平面AEC.(2)过点O作OF⊥PA,垂足为F,连接BF,FD,PO,易知PO⊥平面ABCD.在Rt△POA中,PO=1,AO=3,PA=2,PO2=PF·PA,∴2PF=1,∴PF=12,FA=32,则PFFA=13.返回目录第11讲 空间中的平行与垂直在菱形ABCD中,BD⊥AC,又因为PO⊥平面ABCD,所以BD⊥PO.又AC∩PO=O,所以BD⊥平面APO,所以PA⊥BD.又OF∩BD=O,所以PA⊥平面BDF.当PFFA=13时,在△POA中过点F作FH∥PO,交AC于H,则FH⊥平面BCD,FH=34PO=34,又S△BCD=12×2×3=3,∴所求体积V=13S△BCD·FH=13×34×3=34.返回目录第11讲 空间中的平行与垂直例4[配例3使用]在三棱柱ABCA1B1C1中,AB⊥平面BB1C1C,已知BC=1,∠BCC1=π3,AB=CC1=2.(1)求证:C1B⊥平面ABC;(2)设E是CC1的中点,求AE和平面ABC1所成角的正弦值.返回目录第11讲 空间中的平行与垂直解:(1)证明:∵BC=1,∠BCC1=π3,CC1=2,∴BC1=3,则BC2+BC21=CC21,∴BC1⊥BC.∵AB⊥平面BB1C1C,BC1⊂平面BB1C1C,∴BC1⊥AB.∵BC∩AB=B,∴C1B⊥平面ABC.(2)由AB⊥平面BB1C1C,AB⊂平面ABC1,得平面BCC1B1⊥平面ABC1.过点E作BC1的垂线交BC1于点F,则EF⊥平面ABC1.连接AF,则∠EAF即为所求.∵BC⊥BC1,EF⊥BC1,∴BC∥EF.∵E为C1C的中点,∴F为C1B的中点,则EF=12BC=12.又∵AE=5,∴sin∠EAF=125=510.返回目录第第1212讲 空间角讲 空间角核心知识聚焦考点考向探究返回目录第12讲 空间角体验高考体验高考1.[2012·全国卷]已知正方体ABCDA1B1C1D1中,E,F分别为BB1,CC1的中点,那么异面直线①AE与D1F所成角的余弦值为________.[答案]35[解析]连接DF,易知DF∥AE,所以∠DFD1为异面直线AE与D1F所成的角,设正方体的棱长为2,则DF=D1F=5,DD1=2,由余弦定理可得cos∠DFD1=D1F2+DF2-D1D22D1F·DF=5+5-42×5=35.⇒两条异面直线所成的角关键词:异面直线角、相交直线角,如①②.主干知识主干知识核心知识聚焦返回目录第12讲 空间角体验高考体验高考 2.[2014·全国卷改编]已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角②的余弦值为________.[答案]24核心知识聚焦返回目录第12讲 空间角[解析]如图所示,在平面α内过点C作CF∥AB,过点F作FE⊥β,垂足为点E,连接CE,则CE⊥l,所以∠ECF=60°.过点E作D1E⊥CE,交CD于点D1,连接FD1.不妨设FC=2a,则CE=a,EF=3a.因为∠ACD=135°,所以∠DCE=45°,所以,在Rt△D1CE中,D1E=CE=a,CD1=2a,∴FD1=2a,∴cos∠D1CF=4a2+2a2-4a22×2a×2a=24.核心知识聚焦返回目录第12讲 空间角体验高考体验高考 3.[2013·全国卷改编]已知正四棱柱ABCDA1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角③的正弦值等于________.⇒直线与平面所成的角关键词:平面的垂线,如③④.主干知识主干知识[答案]23核心知识聚焦返回目录第12讲 空间角[解析]如图所示,连接AC,交BD于点O.由于BO⊥OC,BO⊥CC1,可得BO⊥平面OCC1,从而平面OCC1⊥平面BDC1,过点C作OC1的垂线交OC1于点E,根据面面垂直的性质定理可得CE⊥平面BDC1,∠CDE即为所求的线面角.设AB=2,则OC=2,OC1=18=32,所以CE=CC1·OCOC1=4232=43,所以sin∠CDE=CECD=23.核心知识聚焦返回目录第12讲 空间角体验高考体验高考 4.[2013·浙江卷改编]如图121所示,在四棱锥PABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=7,PA=3,∠ABC=120°,G为线段PC的中点,则DG与平面APC所成的角④的正切值为________.图121[答案]433核心知识聚焦返回目录第12讲 空间角[解析]设点O为AC,BD的交点.由AB=BC,AD=CD,得BD是线段AC的中垂线.所以O为AC的中点,BD⊥AC.又因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD,所以BD⊥平面APC.连接OG,则DG在平面APC内的射影为OG,所以∠OGD是DG与平面APC所成的角.由题意得OG=12PA=32.在△ABC中,AC=AB2+BC2-2AB·BC·cos∠ABC=23,所以OC=12AC=3.在Rt△OCD中,OD=CD2-OC2=2.在Rt△OGD中,tan∠OGD=ODOG=433.所以DG与平面APC所成的角的正切值为433.核心知识聚焦返回目录第12讲 空间角体验高考体验高考 5.[2014·湖南卷改编]如图122所示,四棱柱ABCDA1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.若∠CBA=60°,则二面角⑤C1OB1D的余弦值为________.图122⇒平面与平面所成的角关键词:要构造二面角的平面角,如⑤⑥.主干知识主干知识[答案]25719核心知识聚焦返回目录第12讲 空间角体验高考体验高考 6.[2014·全国卷改编]如图123所示,三棱柱ABCA1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.设直线AA1与平面BCC1B1的距离为3,则二面角⑥A1ABC的余弦值为________.图123核心知识聚焦[答案]14返回目录[解析](1)证明:因为A1D⊥平面ABC,A1D⊂平面AA1C1C,故平面AA1C1C⊥平面ABC.又BC⊥AC,平面AA1C1C∩平面ABC=AC,所以BC⊥平面AA1C1C.连接A1C,因为侧面AA1C1C为菱形,故AC1⊥A1C.由三垂线定理得AC1⊥A1B.(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1,故平面AA1C1C⊥平面BCC1B1.连接A1C,作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.第12讲 空间角核心知识聚焦返回目录又直线AA1∥平面BCC1B1,因而A1E为直线AA1到平面BCC1B1的距离,即A1E=3.因为A1C为∠ACC1的平分线,故A1D=A1E=3.作DF⊥AB,F为垂足,连接A1F.由三垂线定理得A1F⊥AB,故∠A1FD为二面角A1ABC的平面角.由AD=AA21-A1D2=1,得D为AC的中点,所以DF=55,tan∠A1FD=A1DDF=15,所以cos∠A1FD=14.所以二面角A1ABC的大小为arccos14.第12讲 空间角核心知识聚焦返回目录第12讲 空间角————教师教师知识必备知识必备———— 知识必备空间角定义特殊情况范围两直线平行时,角的大小为0°线线角把两异面直线平移到相交时,两相交直线所成的角所成角为90°时,称两直线垂直0,π2线面平行或线在平面内时,线面角为0°线面角平面的一条斜线和它在平面上的射影所成的锐角线面垂直时,线面角为90°0,π2两个半平面重合时为0°两个半平面成为一个平面时为180°空间角二面角和平面角在二面角的棱上任取一点,在两个半平面内分别作垂直于棱的射线,这两条射线所成的角当二面角为90°时,称两个平面垂直0,π返回目录第12讲 空间角►考点一两直线所成的角两直线所成的角——两条异面直线所成的角题型:选择、填空分值:5-6分难度:基础热点:两条异面直线所成的角考点考向探究返回目录第12讲 空间角例1[2014·全国卷]已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为()A.16B.36C.13D.33[答案]B考点考向探究返回目录第12讲 空间角[解析]如图所示,取AD的中点F,连接EF,CF,则EF∥BD,故EF与CE所成的角即为异面直线CE与BD所成的角.设正四面体的棱长为2,则CE=CF=3,EF=1.在△CEF中,cos∠CEF=CE2+EF2-CF22CE·EF=3+1-32×3×1=36,所以异面直线CE与BD所成角的余弦值为36.考点考向探究返回目录第12讲 空间角[小结]求两异面直线所成角的关键就是通过作平行线,把异面直线角转化为平面上的相交直线的角,即化空间问题为平面问题.考点考向探究返回目录 第12讲 空间角变式题[2014·湖南卷]如图124所示,已知二面角αMNβ的大小为60°,菱形ABCD在面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O.图124(1)证明:AB⊥平面ODE;(2)求异面直线BC与OD所成角的余弦值.考点考向探究返回目录 第12讲 空间角解:(1)证明:如图所示,因为DO⊥α,AB⊂α,所以DO⊥A.连接BD,由题设知,△ABD是正三角形,又E是AB的中点,所以DE⊥AB.而DO∩DE=D,故AB⊥平面ODE.考点考向探究返回目录第12讲 空间角(2)因为BC∥AD,所以BC与OD所成的角等于AD与OD所成的角,即∠ADO是BC与OD所成的角.由(1)知,AB⊥平面ODE,所以AB⊥OE.又DE⊥AB,于是∠DEO是二面角αMNβ的平面角,从而∠DEO=60°.不妨设AB=2,则AD=2,易知DE=3.在Rt△DOE中,DO=DE·sin60°=32.连接AO,在Rt△AOD中,cos∠ADO=DOAD=322=34.故异面直线BC与OD所成角的余弦值为34.考点考向探究返回目录第12讲 空间角►考点二直线与平面所成的角直线与平面所成的角——直线与平面所成的角题型:选择、填空分值:5分难度:中等热点:直线与平面所成的角考点考向探究返回目录第12讲 空间角例2如图125所示,在四棱锥ABCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=2.图125(1)证明:AC⊥平面BCDE;(2)求直线AE与平面ABC所成的角的正切值.考点考向探究返回目录 第12讲 空间角考点考向探究解:(1)证明:连接BD,在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=2,由AC=2,AB=2,得AB2=AC2+BC2,即AC⊥BC.又平面ABC⊥平面BCDE,从而AC⊥平面BCDE.考点考向探究返回目录 第12讲 空间角考点考向探究(2)在直角梯形BCDE中,由BD=BC=2,DC=2,得BD⊥BC.又平面ABC⊥平面BCDE,所以BD⊥平面ABC.作EF∥BD,与CB的延长线交于点F,连接AF,则EF⊥平面ABC.所以∠EAF是直线AE与平面ABC所成的角.在Rt△BEF中,由EB=1,∠EBF=π4,得EF=22,BF=22.考点考向探究返回目录 第12讲 空间角在Rt△ACF中,由AC=2,CF=322,得AF=262.在Rt△AEF中,由EF=22,AF=262,得tan∠EAF=1313.所以,直线AE与平面ABC所成的角的正切值是1313.考点考向探究返回目录 第12讲 空间角[小结]要求直线与平面所成的角,关键要找到该平面的垂线,构造一个直角三角形,最后解这个直角三角形.考点考向探究返回目录 第12讲 空间角考点考向探究变式题如图126所示,在四棱锥PABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=2,∠ABC=45°,点E在PC上,AE⊥PC.图126(1)证明:AE⊥平面PCD;(2)当PA=2时,求直线AD与平面ABE所成角的正弦值.考点考向探究返回目录 第12讲 空间角解:(1)证明:连接AC,∵AB=1,BC=2,∠ABC=45°,∴AB⊥AC.∵PA⊥平面ABCD,∴PA⊥AB.又∵AC∩AP=A,∴AB⊥平面PAC.又∵AB∥CD,∴CD⊥平面PAC,∴CD⊥AE.又∵AE⊥PC,PC∩CD=C,∴AE⊥平面PCD.考点考向探究返回目录 第12讲 空间角(2)∵AD∥BC,∴直线BC与平面ABE所成的角即为所求角.由(1)知AB⊥PC,又AE⊥PC,且AB∩AE=A,∴PC⊥平面ABE,∴∠CBE是直线BC与平面ABE所成的角.∵在Rt△PAC中,CE=33,∴在Rt△CBE中,sin∠CBE=CECB=332=66,即直线AD与平面ABE所成角的正弦值为66.考点考向探究返回目录 第12讲 空间角►考点三平面与平面所成的角二面角——二面角题型:解答分值:5分难度:较难热点:二面角的大小考点考向探究返回目录 第12讲 空间角例3如图127所示,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足:AMAE=ANAP=λ(0<λ<1).图127(1)求证:MN∥平面ABC.(2)当λ取何值时,平面ABC与平面MNC所成的锐二面角的大小为45°?考点考向探究返回目录第12讲 空间角解:方法一:(1)证明:由AMAE=ANAP=λ,得MN∥PE.又依题意PE∥BC,所以MN∥BC.因为MN⊄平面ABC,BC⊂平面ABC,所以MN∥平面ABC.(2)由(1)知MN∥BC,故C,B,M,N共面,则平面ABC与平面MNC所成的锐二面角为二面角NCBA.因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,且CB⊥AC,所以CB⊥平面PAC,故CB⊥CN,所以∠NCA为二面角NCBA的平面角,所以∠NCA=45°.在△NCA中,ANAC=sin45°sin75°=226+24=3-1,所以λ=ANAP=3-1.考点考向探究返回目录第12讲 空间角方法二:(1)证明:如图所示,以点C为原点,建立空间直角坐标系Cxyz,不妨设CA=1,CB=t(t>0),PE→=μCB→,则C(0,0,0),A(1,0,0),B(0,t,0),P12,0,32,E12,μt,32.考点考向探究返回目录第12讲 空间角由AMAE=ANAP=λ,得M1-12λ,λμt,32λ,N1-12λ,0,32λ,MN→=(0,-λμt,0).易知n0=(0,0,1)是平面ABC的一个法向量,因为n0·MN→=0,所以n0⊥MN→.又因为MN⊄平面ABC,所以MN∥平面ABC.(2)由(1)知MN→=(0,-λμt,0),CM→=1-12λ,λμt,32λ,设平面CMN的法向量n1=(x1,y1,z1),则n1·MN→=0,n1·CM→=0,考点考向探究返回目录第12讲 空间角可取n1=1,0,λ-23λ.设平面ABC与平面MNC所成的锐二面角为θ.由|cosθ|=|n0·n1||n0|·|n1|,θ=45°可得λ-23λ1+(λ-2)23λ2=22,即2λ2+4λ-4=0,解得λ=3-1(将λ=-1-3舍去),故λ=3-1.考点考向探究返回目录第12讲 空间角[小结]求二面角的关键是找出二面角的平面角,然后把平面角放在三角形中通过解三角形求得.考点考向探究返回目录 第12讲 空间角变式题如图128所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.图128(1)求证:BM∥平面PCD;(2)若直线PD与平面PAC所成角的正切值为62,求二面角APDM的正切值.考点考向探究返回目录 第12讲 空间角解:(1)证明:∵△ABC为等边三角形,M为AC的中点,∴BM⊥AC.又∵AC⊥CD,∴在平面ABCD中,有BM∥CD.又∵CD⊂平面PCD,BM⊄平面PCD,∴BM∥平面PCD.(2)∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD.又∵AC⊥CD.PA∩AC=A,∴CD⊥平面PAC.∴直线PD与平面PAC所成角为∠DPC.在Rt△PCD中,tan∠DPC=CDPC=62.考点考向探究返回目录 第12讲 空间角设AP=AB=a,则AC=a,PC=2a,∴CD=62PC=3a.在Rt△ACD中,AD2=AC2+CD2=4a2,∴AD=2a.∵PA⊥平面ABCD,∴平面PAD⊥平面ABCD.在Rt△ACD中,过M作MN⊥AD,垂足为N.又∵平面ABCD∩平面PAD=AD,MN⊂平面ABCD,∴MN⊥平面PAD,∴MN⊥PD.在平面PAD中,过N作NH⊥PD,垂足为H,连接MH,考点考向探究返回目录 第12讲 空间角∵NH∩MN=N,∴PD⊥平面MNH,∴∠MHN为二面角APDM的平面角.在Rt△ACD中,MN=34a,AN=14a,ND=74a.又NHPA=DNPD,PD=5a,∴NH=PA·DNPD=745a,tan∴∠MHN=MNNH=34a745a=157,∴二面角APDM的正切值为157.考点考向探究返回目录第12讲 空间角例1如图所示,在正三棱柱ABCA1B1C1中,已知AB=1,D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则α的余弦值为()A.12B.22C.64D.104————教师备用例题教师备用例题———— 返回目录第12讲 空间角[解析]分别取AC和A1C1的中点E,F,连接B1F,EF,易知B1F⊥平面AA1C1C,过D作DQ∥B1F,与EF交于点Q,连接AQ,则DQ⊥平面AA1C1C,所以∠DAQ为直线AD与平面AA1C1C所成的角,故sinα=DQAD=322=64,则cosα=104.[答案]D返回目录第12讲 空间角例2如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=2,AF=1,M是线段EF的中点.(1)求证:AM∥平面BDE;(2)求二面角ADFB的大小.返回目录第12讲 空间角解:方法一:(1)证明:连接AC,记AC与BD的交点为O,连接OE,∵O,M分别是AC,EF的中点,四边形ACEF是矩形,∴四边形AOEM是平行四边形,∴AM∥OE.∵OE⊂平面BDE,AM⊄平面BDE,∴AM∥平面BDE.返回目录第12讲 空间角(2)在平面AFD中,过A作AS⊥DF于S,连接BS,∵AB⊥AF,AB⊥AD,AD∩AF=A,∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,由三垂线定理得BS⊥DF,∴∠BSA是二面角ADFB的平面角.在Rt△ASB中,AS=63,AB=2,∴tan∠ASB=3,∴∠ASB=60°,故所求二面角ADFB的大小是60°.返回目录第12讲 空间角方法二:(1)证明:建立如图所示的空间直角坐标系Cxyz.连接AC,设AC∩BD=N,连接NE,则点N,E的坐标分别是22,22,0,(0,0,1),∴NE→=-22,-22,1.又点A,M的坐标分别是(2,2,0),22,22,1,∴AM→=-22,-22,1,∴NE→=AM→,且NE→与AM→不共线,∴NE∥AM.又∵NE⊂平面BDE,AM⊄平面BDE,∴AM∥平面BDE.返回目录第12讲 空间角(2)连接NF,∵AF⊥AB,AB⊥AD,AF∩AD=A,∴AB⊥平面ADF,∴AB→=(-2,0,0)为平面DAF的一个法向量.∵NE→·DB→=-22,-22,1·(-2,2,0)=0,NE→·NF→=-22,-22,1·22,22,1=0,∴NE→⊥DB→,NE→⊥NF→,∴NE→为平面BDF的一个法向量.又cosAB→,NE→=12,∴AB→与NE→的夹角是60°,即所求二面角ADFB的大小是60°.返回目录展开内容










 2016年高考理科数学试题(北京卷)+参考答案
2016年高考理科数学试题(北京卷)+参考答案 2019年上海高考数学真题试卷+(答案解析word版)
2019年上海高考数学真题试卷+(答案解析word版) 2017年高考数学知识方法专题10《数学思想第44练 数形结合思想》
2017年高考数学知识方法专题10《数学思想第44练 数形结合思想》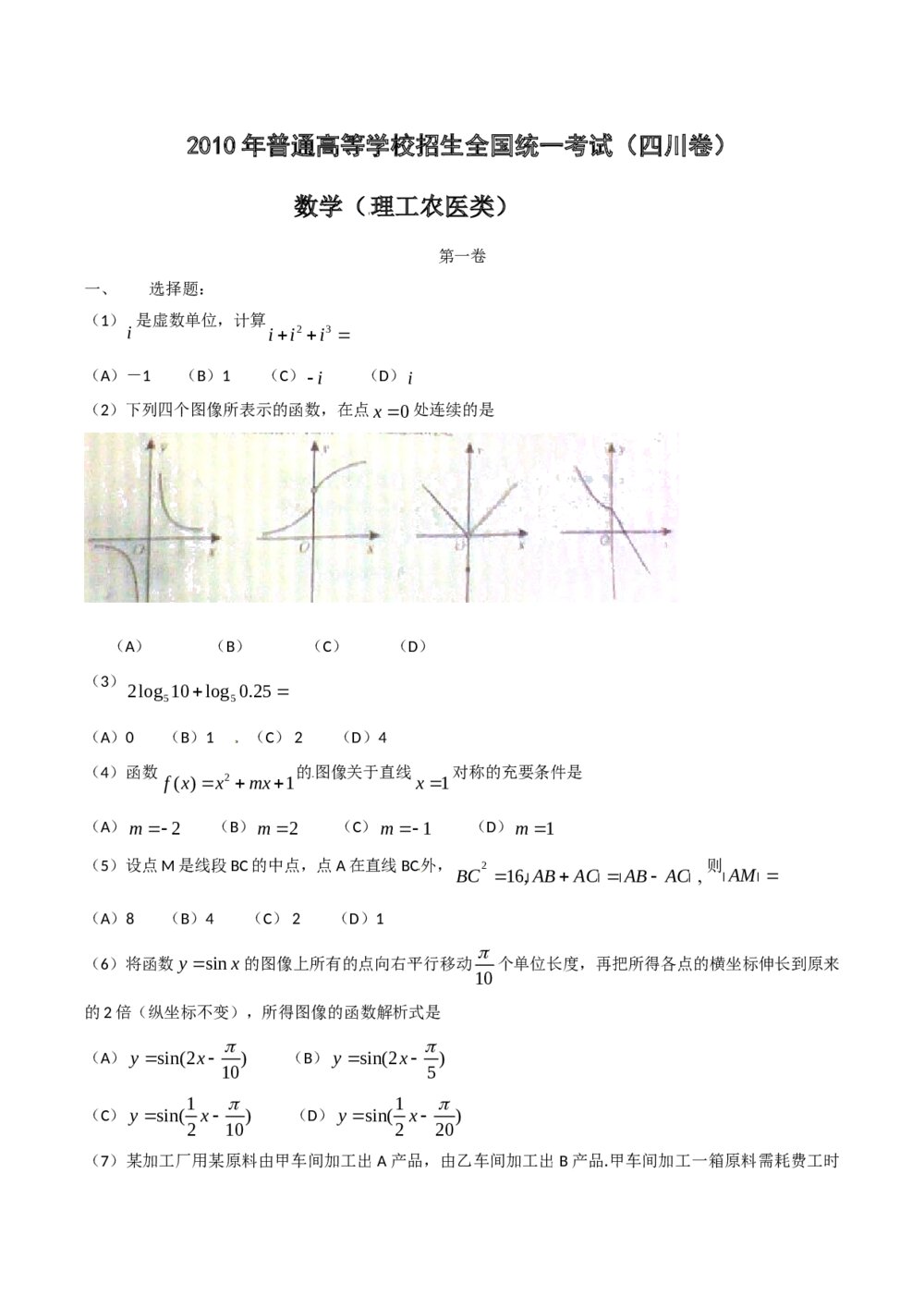 《四川卷》高考数学理科试题试卷word版
《四川卷》高考数学理科试题试卷word版 天水市2015届高考第一轮复习数学(理科)试题试卷+答案
天水市2015届高考第一轮复习数学(理科)试题试卷+答案 2015年泰安市高三期末数学(理科)试题+参考答案
2015年泰安市高三期末数学(理科)试题+参考答案