









试读已结束,还剩1页未读,您可下载完整版后进行离线阅读
《2012北京市朝阳区高三数学试卷+答案(理工类)》是由用户上传到老师板报网,本为文库资料,大小为523.5 KB,总共有11页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 11页
- 523.5 KB
- VIP模板
- doc
- 数字产品不支持退货
北京市朝阳区高三年级第一次综合练习数学试卷(理工类)2012.3(考试时间120分钟满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.复数10i12iA.42iB.42iC.24iD.24i2.已知平面向量,ab满足()=3aa+b,且2,1==ab,则向量a与b的夹角为A.6B.3C.3D.63.已知数列{}na的前n项和为nS,且21()nnSanN,则5aA.16B.16C.31D.324.已知平面,直线,,abl,且,ab,则“la且lb”是“l”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.有10件不同的电子产品,其中有2件产品运行不稳定.技术人员对它们进行一一测试,直到2件不稳定的产品全部找出后测试结束,则恰好3次就结束测试的方法种数是()A.16B.24C.32D.486.已知函数()fx是定义在R上的偶函数,且对任意的xR,都有(2)()fxfx.当01x时,2()fxx.若直线yxa与函数()yfx的图象在[0,2]内恰有两个不同的公共点,则实数a的值是A.0B.0或12C.14或12D.0或147.某工厂生产的A种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一年A种产品定价为每件70元,年销售量为11.8万件.从第二年开始,商场对A种产品征收销售额的%x的管理费(即销售100元要征收x元),于是该产品定价每件比第一年增加了70%1%xx元,预计年销售量减少x万件,要使第二年商场在A种产品经营中收取的管理费不少于14万元,则x的取值范围是A.2B.6.5C.8.8D.108.已知点集22(,)48160Axyxyxy,(,)4,Bxyyxmm是常数,点集A所表示的平面区域与点集B所表示的平面区域的边界的交点为,MN.若点(,4)Dm在点集A所表示的平面区域内(不在边界上),则△DMN的面积的最大值是A.1B.2C.22D.4第二部分(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.已知双曲线的方程为2213xy,则此双曲线的离心率为,其焦点到渐近线的距离为.10.已知某几何体的三视图如图所示,则该几何体的体积为.(第10题图)(第11题图)11.执行如图所示的程序框图,若输入k的值是4,则输出S的值是.12.在极坐标系中,曲线23sin和cos1相交于点,AB,则线段AB的中点E到极点的距离是.13.已知函数213(),2,()24log,02.xxfxxx若函数()()gxfxk有两个不同的零点,则实数k的取值范围是.14.已知△ABC中,90,3,4CACBC.一个圆心为M,半径为14的圆在△21133正视图侧视图俯视图21开始输入kS=0,i=11+(1)SSiii=i+1?ik输出S结束是否ABC内,沿着△ABC的边滚动一周回到原位.在滚动过程中,圆M至少与△ABC的一边相切,则点M到△ABC顶点的最短距离是,点M的运动轨迹的周长是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上.15.(本小题满分13分)已知函数π()cos()4fxx.(Ⅰ)若72()10f,求sin2的值;(II)设()2gxfxfx,求函数()gx在区间ππ,63上的最大值和最小值.16.(本小题满分13分)某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.(Ⅰ)下表是这次考试成绩的频数分布表,求正整数a,b的值;区间[75,80)[80,85)[85,90)[90,95)[95,100]人数50a350300b(II)现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析,求其中成绩为优秀的学生人数;(Ⅲ)在(II)中抽取的40名学生中,要随机选取2名学生参加座谈会,记“其中成绩为优秀的人数”为X,求X的分布列与数学期望.17.(本小题满分14分)在如图所示的几何体中,四边形ABCD为平行四边形,=90ABD,EB平面ABCD,EF//AB,=2AB,=3,=1EBEF,=13BC,且M是BD的中点.(Ⅰ)求证:EM//平面ADF;(Ⅱ)求二面角D-AF-B的大小;(Ⅲ)在线段EB上是否存在一点P,使得CP与AF所成的角为30?若存在,求出BP的长度;若不存在,请说明理由.18.(本小题满分13分)85809010095O频率组距分数750.010.020.030.040.050.060.07CAFEBMD设函数2e(),1axfxaxR.(Ⅰ)当1a时,求曲线()yfx在点(0,(0))f处的切线方程;(Ⅱ)求函数)(xf单调区间.19.(本小题满分14分)已知椭圆2222:1(0)xyCabab的两个焦点分别为1(2,0)F,2(2,0)F.点(1,0)M与椭圆短轴的两个端点的连线相互垂直.(Ⅰ)求椭圆C的方程;(Ⅱ)已知点N的坐标为(3,2),点P的坐标为(,)(3)mnm.过点M任作直线l与椭圆C相交于A,B两点,设直线AN,NP,BN的斜率分别为1k,2k,3k,若1322kkk,试求,mn满足的关系式.20.(本小题满分13分)已知各项均为非负整数的数列001:,,,nAaaa()nN,满足00a,1naan.若存在最小的正整数k,使得(1)kakk,则可定义变换T,变换T将数列0A变为数列00111():1,1,,1,0,,,kknTAaaaaa.设1()iiATA,0,1,2i.(Ⅰ)若数列0:0,1,1,3,0,0A,试写出数列5A;若数列4:4,0,0,0,0A,试写出数列0A;(Ⅱ)证明存在唯一的数列0A,经过有限次T变换,可将数列0A变为数列,0,0,,0nn个;(Ⅲ)若数列0A,经过有限次T变换,可变为数列,0,0,,0nn个.设1mmmnSaaa,1,2,,mn,求证[](1)1mmmSaSmm,其中[]1mSm表示不超过1mSm的最大整数.北京市朝阳区高三年级第一次综合练习数学试卷(理工类)2012.3一、选择题:题号(1)(2)(3)(4)(5)(6)(7)(8)答案ACBBCDDB二、填空题:题号(9)(10)(11)(12)(13)(14)答案2331323423(,1)4249三、解答题:(15)(本小题满分13分)解:(Ⅰ)因为π72()cos()410f,所以272(cossin)210,所以7cossin5.平方得,22sin2sincoscos=4925,所以24sin225.……………6分(II)因为π()2gxfxfx=ππcos()cos()44xx=22(cossin)(cossin)22xxxx=221(cossin)2xx=1cos22x.……………10分当ππ,63x时,π2π2,33x.所以,当0x时,()gx的最大值为12;当π3x时,()gx的最小值为14.……………13分(16)(本小题满分13分)解:(Ⅰ)依题意,0.0451000200,0.0251000100ab.……………4分(Ⅱ)设其中成绩为优秀的学生人数为x,则350300100401000x,解得:x=30,即其中成绩为优秀的学生人数为30名.……………7分(Ⅲ)依题意,X的取值为0,1,2,2102403(0)52CPXC,1110302405(1)13CCPXC,23024029(2)52CPXC,所以X的分布列为X012P3525132952352930125213522EX,所以X的数学期望为32.……………13分(17)(本小题满分14分)证明:(Ⅰ)取AD的中点N,连接MN,NF.在△DAB中,M是BD的中点,N是AD的中点,所以1=2MN//AB,MNAB,又因为1=2EF//AB,EFAB,所以MN//EF且MN=EF.所以四边形MNFE为平行四边形,所以EM//FN.又因为FN平面ADF,EM平面ADF,故EM//平面ADF.……………4分解法二:因为EB平面ABD,ABBD,故以B为原点,建立如图所示的空间直角坐标系-Bxyz.……………1分由已知可得(0,0,0),(0,2,0),(3,0,0),BAD3(3,-2,0),(0,0,3),(0,1,3),(,0,0)2CEFM(Ⅰ)3=(,0,-3)(3,-2,0)2EM,AD=,=(0,-1,3)AF.……………2分设平面ADF的一个法向量是()x,y,zn.由0,0,ADAFnn得323x-y=0,-y+z=0.令y=3,则(2,3,3)n.……………3分又因为3(,0,-3)(2,3,3)=3+0-3=02EMn,所以EMn,又EM平面ADF,所以//EM平面ADF.……………4分(Ⅱ)由(Ⅰ)可知平面ADF的一个法向量是(2,3,3)n.因为EB平面ABD,所以EBBD.又因为ABBD,所以BD平面EBAF.故(3,0,0)BD是平面EBAF的一个法向量.NCAFEBMDzCAFEBMDxy所以1cos<=2BDBD,BDnnn,又二面角D-AF-B为锐角,故二面角D-AF-B的大小为60.……………10分(Ⅲ)假设在线段EB上存在一点P,使得CP与AF所成的角为30.不妨设(0,0,t)P(03t),则=(3,-2,-),=(0,-1,3)PCAFt.所以2-3cos<22PCAFtPC,AFPCAFt+13,由题意得2-33222tt+13,化简得4335t,解得35043t.所以在线段EB上不存在点P,使得CP与AF所成的角为30.…………14分(18)(本小题满分13分)解:因为2e(),1axfxx所以222e(2)()(1)axaxxafxx.(Ⅰ)当1a时,2e()1xfxx,222e(21)()(1)xxxfxx,所以(0)1,f(0)1f.所以曲线()yfx在点(0,(0))f处的切线方程为10xy.……………4分(Ⅱ)因为222222e(2)e()(2)(1)(1)axaxaxxafxaxxaxx,……………5分(1)当0a时,由()0fx得0x;由()0fx得0x.所以函数()fx在区间(,0)单调递增,在区间(0,)单调递减.……………6分(2)当0a时,设2()2gxaxxa,方程2()20gxaxxa的判别式2444(1)(1),aaa……………7分①当01a时,此时0.由()0fx得211axa,或211axa;由()0fx得221111aaxaa.所以函数()fx单调递增区间是211(,)aa和211(,)aa,单调递减区间221111(,)aaaa.……………9分②当1a时,此时0.所以()0fx,所以函数()fx单调递增区间是(,).……………10分③当10a时,此时0.由()0fx得221111aaxaa;由()0fx得211axa,或211axa.所以当10a时,函数()fx单调递减区间是211(,)aa和211(,)aa,单调递增区间221111(,)aaaa.……………12分④当1a时,此时0,()0fx,所以函数()fx单调递减区间是(,).…………13分(19)(本小题满分14分)解:(Ⅰ)依题意,2c,1b,所以223abc.故椭圆C的方程为2213xy.……………4分(Ⅱ)①当直线l的斜率不存在时,由221,13xxy解得61,3xy.不妨设6(1,)3A,6(1,)3B,因为13662233222kk,又1322kkk,所以21k,所以,mn的关系式为213nm,即10mn.………7分②当直线l的斜率存在时,设直线l的方程为(1)ykx.将(1)ykx代入2213xy整理化简得,2222(31)6330kxkxk.设11(,)Axy,22(,)Bxy,则2122631kxxk,21223331kxxk.………9分又11(1)ykx,22(1)ykx.所以12122113121222(2)(3)(2)(3)33(3)(3)yyyxyxkkxxxx12211212[2(1)](3)[2(1)](3)3()9kxxkxxxxxx121212122(42)()6123()9kxxkxxkxxxx222222223362(42)6123131336393131kkkkkkkkkkk222(126)2.126kk………12分所以222k,所以2213nkm,所以,mn的关系式为10mn.………13分综上所述,,mn的关系式为10mn.………14分(20)(本小题满分13分)解:(Ⅰ)若0:0,1,1,3,0,0A,则1:1,0,1,3,0,0A;2:2,1,2,0,0,0A;3:3,0,2,0,0,0A;4:4,1,0,0,0,0A;5:5,0,0,0,0,0A.若4:4,0,0,0,0A,则3:3,1,0,0,0A;2:2,0,2,0,0A;1:1,1,2,0,0A;0:0,0,1,3,0A.………4分(Ⅱ)先证存在性,若数列001:,,,nAaaa满足0ka及0(01)iaik,则定义变换1T,变换1T将数列0A变为数列10()TA:01111,1,,1,,,,kknaaakaa.易知1T和T是互逆变换.………5分对于数列,0,0,,0n连续实施变换1T(一直不能再作1T变换为止)得,0,0,,0n1T1,1,0,,0n1T2,0,2,0,,0n1T3,1,2,0,,0n1T1T01,,,naaa,则必有00a(若00a,则还可作变换1T).反过来对01,,,naaa作有限次变换T,即可还原为数列,0,0,,0n,因此存在数列0A满足条件.下用数学归纳法证唯一性:当1,2n是显然的,假设唯一性对1n成立,考虑n的情形.假设存在两个数列01,,,naaa及01,,,nbbb均可经过有限次T变换,变为,0,,0n,这里000ab,1212nnaaabbbn若0nan,则由变换T的定义,不能变为,0,,0n;若nan,则120naaa,经过一次T变换,有0,0,,0,nT1,1,,1,0由于3n,可知1,1,,1,0(至少3个1)不可能变为,0,,0n.所以0na,同理0nb令01,,,naaaT121,,,,naaa,01,,,nbbbT121,,,,nbbb,则0nnab,所以1211naaan,1211nbbbn.因为110,,,naaT有限次-1,0,,0n,110,,,nbbT有限次-1,0,,0n,故由归纳假设,有iiab,1,2,,1in.再由T与1T互逆,有01,,,naaaT111,,,,0naa,01,,,nbbbT111,,,,0nbb,所以iiab,1,2,,in,从而唯一性得证.………9分(Ⅲ)显然iai(1,2,,)in,这是由于若对某个0i,00iai,则由变换的定义可知,0ia通过变换,不能变为0.由变换T的定义可知数列0A每经过一次变换,kS的值或者不变,或者减少k,由于数列0A经有限次变换T,变为数列,0,,0n时,有0mS,1,2,,mn,所以mmSmt(mt为整数),于是1mmmSaS1(1)mmamt,0mam,所以ma为mS除以1m后所得的余数,即[](1)1mmmSaSmm.………13分展开内容










 徐州市高三第三次数学模拟考试word版
徐州市高三第三次数学模拟考试word版 2018年全国统一高考数学试卷(文科)(新课标ⅰ)+参考答案解析
2018年全国统一高考数学试卷(文科)(新课标ⅰ)+参考答案解析 2016年高考文科数学试卷(新课标Ⅰ)+(含答案)
2016年高考文科数学试卷(新课标Ⅰ)+(含答案)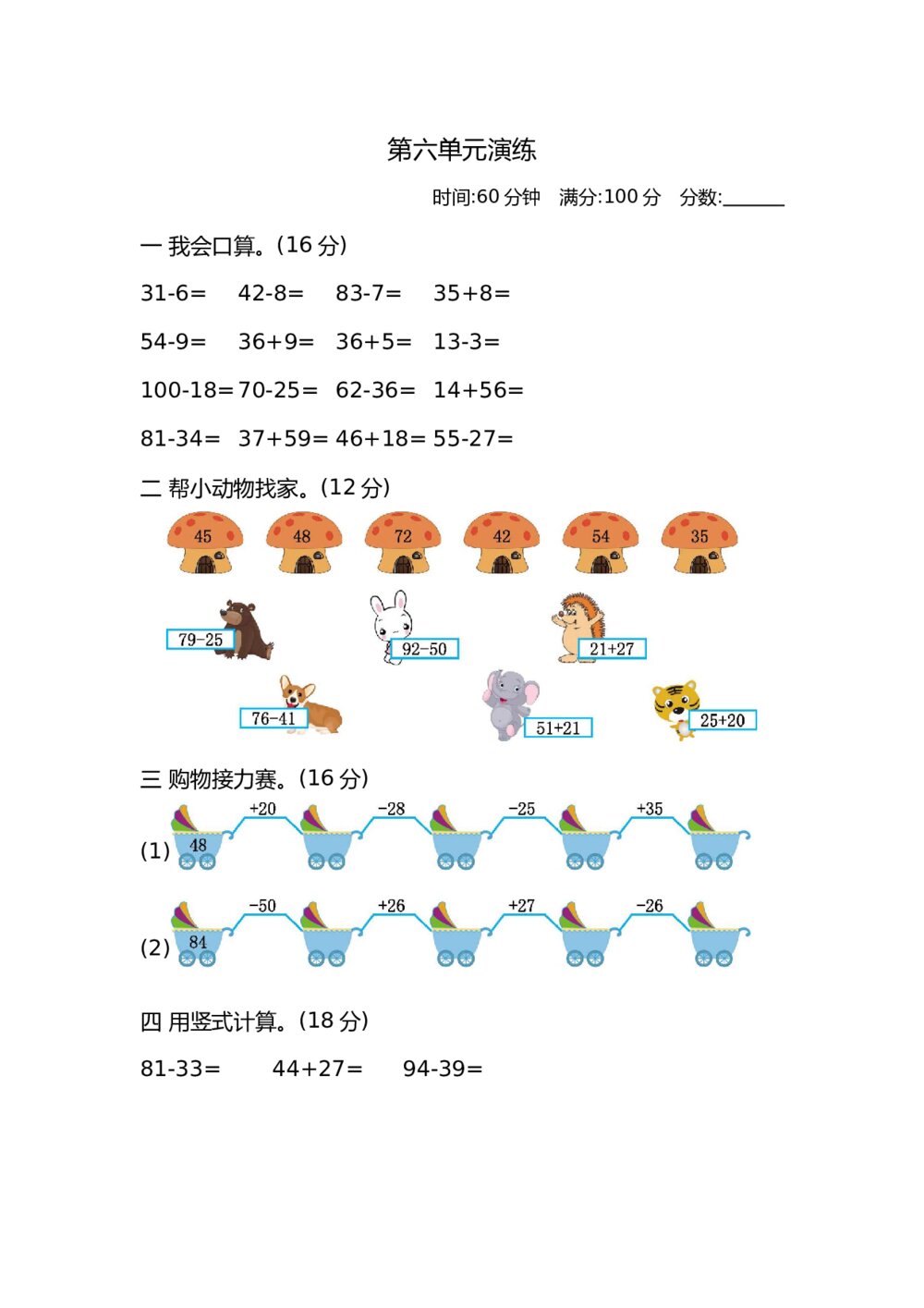 新北师大版小学一年级下册数学第六单元检测试卷有答案
新北师大版小学一年级下册数学第六单元检测试卷有答案 2011年高考一轮课时训练(理)10.2双曲线+参考答案 (通用版)
2011年高考一轮课时训练(理)10.2双曲线+参考答案 (通用版) 2022-2023学年江西省南昌市七年级(上册)期末数学试卷word版
2022-2023学年江西省南昌市七年级(上册)期末数学试卷word版