









试读已结束,还剩48页未读,您可下载完整版后进行离线阅读
《最新6年高考4年模拟试题试卷--第五章第二节解三角形(答案解析)》是由用户上传到老师板报网,本为文库资料,大小为2.92 MB,总共有58页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 58页
- 2.92 MB
- VIP模板
- doc
- 数字产品不支持退货
第五章平面向量、解三角形第二节解三角形第一部分六年高考荟萃2010年高考题一、选择题1.(2010上海文)18.若△ABC的三个内角满足sin:sin:sin5:11:13ABC,则△ABC(A)一定是锐角三角形.(B)一定是直角三角形.(C)一定是钝角三角形.(D)可能是锐角三角形,也可能是钝角三角形.【答案】C解析:由sin:sin:sin5:11:13ABC及正弦定理得a:b:c=5:11:13由余弦定理得0115213115cos222c,所以角C为钝角2.(2010湖南文)7.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=2a,则A.a>bB.a<bC.a=bD.a与b的大小关系不能确定【命题意图】本题考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题3.(2010江西理)7.E,F是等腰直角△ABC斜边AB上的三等分点,则tanECF()A.1627B.23C.33D.34【答案】D【解析】考查三角函数的计算、解析化应用意识。解法1:约定AB=6,AC=BC=32,由余弦定理CE=CF=10,再由余弦定理得4cos5ECF,解得3tan4ECF解法2:坐标化。约定AB=6,AC=BC=32,F(1,0),E(-1,0),C(0,3)利用向量的夹角公式得4cos5ECF,解得3tan4ECF。4.(2010北京文)(7)某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为(A)2sin2cos2;(B)sin3cos3(C)3sin3cos1;(D)2sincos1【答案】A5.(2010天津理)(7)在△ABC中,内角A,B,C的对边分别是a,b,c,若223abbc,sin23sinCB,则A=(A)030(B)060(C)0120(D)0150【答案】A【解析】本题主要考查正弦定理与余弦定理的基本应用,属于中等题。由由正弦定理得232322cbcbRR,所以cosA=2222+c-a322bbccbcbc=323322bcbcbc,所以A=300【温馨提示】解三角形的基本思路是利用正弦、余弦定理将边化为角运算或将角化为边运算。6.(2010湖南理)6、在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,2ca,则A、a>bB、a,,>ACOCOCACAC故且对于线段上任意点P有OPOC,而小艇的最高航行速度只能达到30海里/小时,故轮船与小艇不可能在A、C(包含C)的任意位置相遇,设COD=(0<<90),103tanRtCODCD则在中,,OD=103cos,由于从出发到相遇,轮船与小艇所需要的时间分别为10103tan30t和103costv,所以10103tan30103cosv,解得1533,30,sin(+30)sin(+30)2vv又故,从而30<90,30tan由于时,取得最小值,且最小值为33,于是当30时,10103tan30t取得最小值,且最小值为23。此时,在OAB中,20OAOBAB,故可设计航行方案如下:航行方向为北偏东30,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。(2010安徽理数)16、(本小题满分12分)设ABC是锐角三角形,,,abc分别是内角,,ABC所对边长,并且22sinsin()sin()sin33ABBB。(Ⅰ)求角A的值;(Ⅱ)若12,27ABACa,求,bc(其中bc)。8.(2010江苏卷)17、(本小题满分14分)某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=,∠ADE=。(1)该小组已经测得一组、的值,tan=1.24,tan=1.20,请据此算出H的值;(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使与之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,-最大?[解析]本题主要考查解三角形的知识、两角差的正切及不等式的应用。(1)tantanHHADAD,同理:tanHAB,tanhBD。AD—AB=DB,故得tantantanHHh,解得:tan41.24124tantan1.241.20hH。因此,算出的电视塔的高度H是124m。(2)由题设知dAB,得tan,tanHHhHhdADDBd,2tantantan()()1tantan()1HHhhdhddHHhHHhdHHhdddd()2()HHhdHHhd,(当且仅当()125121555dHHh时,取等号)故当555d时,tan()最大。因为02,则02,所以当555d时,-最大。故所求的d是555m。9.(2010江苏卷)23.(本小题满分10分)已知△ABC的三边长都是有理数。(1)求证cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数。[解析]本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。(方法一)(1)证明:设三边长分别为,,abc,222cos2bcaAbc,∵,,abc是有理数,222bca是有理数,分母2bc为正有理数,又有理数集对于除法的具有封闭性,∴2222bcabc必为有理数,∴cosA是有理数。(2)①当1n时,显然cosA是有理数;当2n时,∵2cos22cos1AA,因为cosA是有理数,∴cos2A也是有理数;②假设当(2)nkk时,结论成立,即coskA、cos(1)kA均是有理数。当1nk时,cos(1)coscossinsinkAkAAkAA,1cos(1)coscos[cos()cos()]2kAkAAkAAkAA,11cos(1)coscoscos(1)cos(1)22kAkAAkAkA,解得:cos(1)2coscoscos(1)kAkAAkA∵cosA,coskA,cos(1)kA均是有理数,∴2coscoscos(1)kAAkA是有理数,∴cos(1)kA是有理数。即当1nk时,结论成立。综上所述,对于任意正整数n,cosnA是有理数。(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知222cos2ABACBCAABAC是有理数。(2)用数学归纳法证明cosnA和sinsinAnA都是有理数。①当1n时,由(1)知cosA是有理数,从而有2sinsin1cosAAA也是有理数。②假设当(1)nkk时,coskA和sinsinAkA都是有理数。当1nk时,由cos(1)coscossinsinkAAkAAkA,sinsin(1)sin(sincoscossin)(sinsin)cos(sinsin)cosAkAAAkAAkAAAkAAkAA,及①和归纳假设,知cos(1)kA和sinsin(1)AkA都是有理数。即当1nk时,结论成立。综合①、②可知,对任意正整数n,cosnA是有理数。2009年高考题1.(2009年广东卷文)已知ABC中,CBA,,的对边分别为,,abc若62ac且75Ao,则b()A.2B.4+23C.4—23D.62答案A解析000000026sinsin75sin(3045)sin30cos45sin45cos304A由62ac可知,075C,所以030B,1sin2B由正弦定理得261sin2sin2264abBA,故选A2.(2009全国卷Ⅱ文)已知△ABC中,12cot5A,则cosA()A.1213B.513C.513D.1213答案D解析本题考查同角三角函数关系应用能力,先由cotA=125知A为钝角,cosA<0排除A和B,再由1312cos1cossin,512sincoscot22AAAAAA求得和.3.(2009全国卷Ⅱ理)已知ABC中,12cot5A,则cosA()A.1213B.513C.513D.1213答案D解析已知ABC中,12cot5A,(,)2A.221112cos1351tan1()12AA故选D.4.(2009湖南卷文)在锐角ABC中,1,2,BCBA则cosACA的值等于,AC的取值范围为.答案 2)3,2(解析设,2.AB由正弦定理得,12.sin2sin2coscosACBCACAC由锐角ABC得0290045,又01803903060,故233045cos22,2cos(2,3).AC5.(2009全国卷Ⅰ理)在ABC中,内角A、B、C的对边长分别为a、b、c,已知222acb,且sincos3cossin,ACAC求b分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1)222acb左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)sincos3cossin,ACAC过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.解法一:在ABC中sincos3cossin,ACAC则由正弦定理及余弦定理有:2222223,22abcbcaacabbc化简并整理得:2222()acb.又由已知222acb24bb.解得40(bb或舍).解法二:由余弦定理得:2222cosacbbcA.又222acb,0b.所以2cos2bcA①又sincos3cossinACAC,sincoscossin4cossinACACACsin()4cossinACAC,即sin4cossinBAC由正弦定理得sinsinbBCc,故4cosbcA②由①,②解得4b.评析:从08年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒:两纲中明确不再考的知识和方法了解就行,不必强化训练。6.(2009浙江理)(本题满分14分)在ABC中,角,,ABC所对的边分别为,,abc,且满足25cos25A,3ABAC.(I)求ABC的面积;(II)若6bc,求a的值.解(1)因为25cos25A,234cos2cos1,sin255AAA,又由3ABAC得cos3,bcA5bc,1sin22ABCSbcA(2)对于5bc,又6bc,5,1bc或1,5bc,由余弦定理得2222cos20abcbcA,25a7.(2009浙江文)(本题满分14分)在ABC中,角,,ABC所对的边分别为,,abc,且满足25cos25A,3ABAC.(I)求ABC的面积;(II)若1c,求a的值.解(Ⅰ)531)552(212cos2cos22AA又),0(A,54cos1sin2AA,而353cos...bcAACABACAB,所以5bc,所以ABC的面积为:254521sin21Abc(Ⅱ)由(Ⅰ)知5bc,而1c,所以5b所以5232125cos222Abccba8.(2009北京理)在ABC中,角,,ABC的对边分别为,,,3abcB,4cos,35Ab。(Ⅰ)求sinC的值;(Ⅱ)求ABC的面积.【解析】本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,主要考查基本运算能力.解(Ⅰ)∵A、B、C为△ABC的内角,且4,cos35BA,∴23,sin35CAA,∴231343sinsincossin32210CAAA.(Ⅱ)由(Ⅰ)知3343sin,sin510AC,又∵,33Bb,∴在△ABC中,由正弦定理,得∴sin6sin5bAaB.∴△ABC的面积1163433693sin32251050SabC.9.(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+3)+sin2x.(1)求函数f(x)的最大值和最小正周期.(2)设A,B,C为ABC的三个内角,若cosB=31,1()24cf,且C为锐角,求sinA.解(1)f(x)=cos(2x+3)+sin2x.=1cos213cos2cossin2sinsin233222xxxx所以函数f(x)的最大值为132,最小正周期.(2)()2cf=13sin22C=-41,所以3sin2C,因为C为锐角,所以3C,又因为在ABC中,cosB=31,所以2sin33B,所以2113223sinsin()sincoscossin232326ABCBCBC.10.(2009山东卷文)(本小题满分12分)设函数f(x)=2)0(sinsincos2cossin2xxx在x处取最小值.(1)求.的值;(2)在ABC中,cba,,分别是角A,B,C的对边,已知,2,1ba23)(Af,求角C.解(1)1cos()2sincossinsin2fxxxxsinsincoscossinsinxxxxsincoscossinxxsin()x因为函数f(x)在x处取最小值,所以sin()1,由诱导公式知sin1,因为0,所以2.所以()sin()cos2fxxx(2)因为23)(Af,所以3cos2A,因为角A为ABC的内角,所以6A.又因为,2,1ba所以由正弦定理,得sinsinabAB,也就是sin12sin222bABa,因为ba,所以4B或43B.当4B时,76412C;当43B时,36412C.【命题立意】:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合.10.(2009全国卷Ⅱ文)(本小题满分12分)设△ABC的内角A、B、C的对边长分别为a、b、c,23cos)cos(BCA,acb2,求B.解析:本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB=23(负值舍掉),从而求出B=3。解:由cos(AC)+cosB=32及B=π(A+C)得cos(AC)cos(A+C)=32,cosAcosC+sinAsinC(cosAcosCsinAsinC)=32,sinAsinC=34.又由2b=ac及正弦定理得2sinsinsin,BAC故23sin4B,3sin2B或3sin2B(舍去),于是B=3π或B=23π.又由2bac知ab或cb所以B=3π。11.(2009安徽卷理)在ABC中,sin()1CA,sinB=13.(I)求sinA的值;(II)设AC=6,求ABC的面积.解:(Ⅰ)由2CA,且CAB,∴42BA,∴2sinsin()(cossin)42222BBBA,∴211sin(1sin)23AB,又sin0A,∴3sin3A(Ⅱ)如图,由正弦定理得sinsinACBCBA∴36sin3321sin3ACABCB,又sinsin()sincoscossinCABABAB32261633333∴116sin63232223ABCSACBCC12.(2009安徽卷文)(本小题满分12分)在ABC中,C-A=,sinB=。(I)求sinA的值;(II)设AC=,求ABC的面积。【思路】(1)依据三角函数恒等变形可得关于sinA的式子,这之中要运用到倍角公式(2)应用正弦定理可得出边长,进而用面积公式可求出S.解(1)∵2cAcAB且∴42BA∴2sinsin()(cossin)42222BBBA∴22111sin(cossin)(1sin)22223BBAB又sin0A∴3cos3AABC(2)如图,由正弦定理得sinsinACBCBCBA∴36sin3321sin3ACABCBsinsin()sincoscossin322163333CABABAB又∴116sin63232223SABCACBCC.13.(2009江西卷文)在△ABC中,,,ABC所对的边分别为,,abc,6A,(13)2cb.(1)求C;(2)若13CBCA,求a,b,c.解:(1)由(13)2cb得13sin22sinbBcC则有55sin()sincoscossin666sinsinCCCCC=1313cot2222C得cot1C即4C.(2)由13CBCA推出cos13abC;而4C,即得2132ab,则有2132(13)2sinsinabcbacAC解得2132abc14.(2009江西卷理)△ABC中,,,ABC所对的边分别为,,abc,sinsintancoscosABCAB,sin()cosBAC.(1)求,AC;(2)若33ABCS,求,ac.解:(1)因为sinsintancoscosABCAB,即sinsinsincoscoscosCABCAB,所以sincossincoscossincossinCACBCACB,即sincoscossincossinsincosCACACBCB,得sin()sin()CABC.所以CABC,或()CABC(不成立).即2CAB,得3C,所以.23BA又因为1sin()cos2BAC,则6BA,或56BA(舍去)得5,412AB(2)162sin3328ABCSacBac,又sinsinacAC,即2322ac,得22,23.ac15.(2009天津卷文)在ABC中,ACACBCsin2sin,3,5(Ⅰ)求AB的值。(Ⅱ)求)42sin(A的值。(1)解:在ABC中,根据正弦定理,ABCCABsinsin,于是522sinsinBCABCCAB(2)解:在ABC中,根据余弦定理,得ACABBCACABA2cos222于是AA2cos1sin=55,从而53sincos2cos,54cossin22sin22AAAAAA1024sin2cos4cos2sin)42sin(AAA【考点定位】本题主要考查正弦定理,余弦定理同角的三角函数的关系式,二倍角的正弦和余弦,两角差的正弦等基础知识,考查基本运算能力。16.(2009四川卷文)在ABC中,AB、为锐角,角ABC、、所对的边分别为abc、、,且510sin,sin510AB(I)求AB的值;(II)若21ab,求abc、、的值。解(I)∵AB、为锐角,510sin,sin510AB∴2225310cos1sin,cos1sin510AABB253105102cos()coscossinsin.5105102ABABAB∵0AB∴4AB(II)由(I)知34C,∴2sin2C由sinsinsinabcABC得5102abc,即2,5abcb又∵21ab∴221bb∴1b∴2,5ac17.(2009全国卷Ⅱ理)设ABC的内角A、B、C的对边长分别为a、b、c,3cos()cos2ACB,2bac,求B分析:由3cos()cos2ACB,易想到先将()BAC代入3cos()cos2ACB得3cos()cos()2ACAC。然后利用两角和与差的余弦公式展开得3sinsin4AC;又由2bac,利用正弦定理进行边角互化,得2sinsinsinBAC,进而得3sin2B.故233B或。大部分考生做到这里忽略了检验,事实上,当23B时,由1coscos()2BAC,进而得3cos()cos()212ACAC,矛盾,应舍去。也可利用若2bac则babc或从而舍去23B。不过这种方法学生不易想到。评析:本小题考生得分易,但得满分难。18.(2009辽宁卷文)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为075,030,于水面C处测得B点和D点的仰角均为060,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,21.414,62.449)解:在ACD中,DAC=30°,ADC=60°-DAC=30°,所以CD=AC=0.1又BCD=180°-60°-60°=60°,故CB是CAD底边AD的中垂线,所以BD=BA5分在ABC中,ABCACBCAABsinsin,即AB=2062351sin60sinAC因此,km33.020623BD故B、D的距离约为0.33km。12分19.(2009辽宁卷理)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为075,030,于水面C处测得B点和D点的仰角均为060,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,21.414,62.449)解:在△ABC中,∠DAC=30°,∠ADC=60°-∠DAC=30,所以CD=AC=0.1又∠BCD=180°-60°-60°=60°,故CB是△CAD底边AD的中垂线,所以BD=BA,在△ABC中,,ABCsinCBCAsinAAB即AB=,2062315sinACsin60因此,BD=。km33.020623故B,D的距离约为0.33km。 20.(2009宁夏海南卷理)(本小题满分12分)为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。解:方案一:①需要测量的数据有:A点到M,N点的俯角;B点到M,N的俯角22,;A,B的距离d(如图所示).②第一步:计算AM.由正弦定理212sinsin()dAM ;第二步:计算AN.由正弦定理221sinsin()dAN ;第三步:计算MN.由余弦定理22112cos()MNAMANAMAN.方案二:①需要测量的数据有:A点到M,N点的俯角1,1;B点到M,N点的府角2,2;A,B的距离d(如图所示).②第一步:计算BM.由正弦定理112sinsin()dBM ;第二步:计算BN.由正弦定理121sinsin()dBN ;第三步:计算MN.由余弦定理22222cos()MNBMBNBMBN21.(2009四川卷文)在ABC中,AB、为锐角,角ABC、、所对的边分别为abc、、,且510sin,sin510AB(I)求AB的值;(II)若21ab,求abc、、的值。解(I)∵AB、为锐角,510sin,sin510AB∴2225310cos1sin,cos1sin510AABB253105102cos()coscossinsin.5105102ABABAB∵0AB∴4AB(II)由(I)知34C,∴2sin2C由sinsinsinabcABC得5102abc,即2,5abcb又∵21ab∴221bb∴1b∴2,5ac22.(2009湖北卷文)在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且Acasin23(Ⅰ)确定角C的大小:(Ⅱ)若c=7,且△ABC的面积为233,求a+b的值。解(1)由32sinacA及正弦定理得,2sinsinsin3aAAcC3sin0,sin2ACQABCQ是锐角三角形,3C(2)解法1:7,.3cCQ由面积公式得133sin,6232abab即 ①由余弦定理得22222cos7,73abababab即 ②由②变形得25,5ab2(a+b)故解法2:前同解法1,联立①、②得2222766ababababab=13 消去b并整理得4213360aa解得2249aa或所以2332aabb或故5ab23.(2009宁夏海南卷文)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知50ABm,120BCm,于A处测得水深80ADm,于B处测得水深200BEm,于C处测得水深110CFm,求∠DEF的余弦值。解:作//DMAC交BE于N,交CF于M.22223017010198DFMFDM,222250120130DEDNEN,2222()90120150EFBEFCBC. 在DEF中,由余弦定理,2222221301501029816cos2213015065DEEFDFDEFDEEF.24.(2009湖南卷理).在ABC,已知2233ABACABACBC,求角A,B,C的大小.解设,,BCaACbABc由23ABACABAC得2cos3bcAbc,所以3cos2A又(0,),A因此6A由233ABACBC得23bca,于是23sinsin3sin4CBA所以53sinsin()64CC,133sin(cossin)224CCC,因此22sincos23sin3,sin23cos20CCCCC,既sin(2)03C由A=6知506C,所以3,4233C,从而20,3C或2,3C,既,6C或2,3C故2,,,636ABC或2,,663ABC。25..(2009天津卷理)(在⊿ABC中,BC=5,AC=3,sinC=2sinA(I)求AB的值:(II)求sin24A的值(Ⅰ)解:在△ABC中,根据正弦定理,ABCCABsinsin于是AB=522sinsinBCBCAC(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=5522222ACABBDACAB于是sinA=55cos12A从而sin2A=2sinAcosA=54,cos2A=cos2A-sin2A=53所以sin(2A-4)=sin2Acos4-cos2Asin4=10226.(2009四川卷理)在ABC中,,AB为锐角,角,,ABC所对应的边分别为,,abc,且310cos2,sin510AB(I)求AB的值;(II)若21ab,求,,abc的值。解:(Ⅰ)A、B为锐角,10sin10B,2310cos1sin10Bb又23cos212sin5AA,5sin5A,225cos1sin5AA,253105102cos()coscossinsin5105102ABABAB0AB4AB(Ⅱ)由(Ⅰ)知34C,2sin2C.由正弦定理sinsinsinabcABC得5102abc,即2ab,5cb21abQ,221bb,1b2,5ac27.(2009上海卷文)已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量(,)mab, (sin,sin)nBA,(2,2)pba.(1)若m//n,求证:ΔABC为等腰三角形;(2)若m⊥p,边长c=2,角C=3,求ΔABC的面积.证明:(1)//,sinsin,mnaAbBuvvQ即22ababRR,其中R是三角形ABC外接圆半径,abABC为等腰三角形解(2)由题意可知//0,(2)(2)0mpabbauvuv即abab由余弦定理可知,2224()3abababab2()340abab即4(1)abab舍去11sin4sin3223SabC2005—2008年高考题一、选择题1.(2008福建)在△ABC中,角A、B、C的对边分别为a、b、c,若(a2+c2-b2)tanB=3ac,则角B的值为()A.6B.3C.6或56D.3或23答案D2.(2008海南)如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为()A.185B.43C.23D.87答案D3.(2008陕西)ABC△的内角A、B、C的对边分别为a、b、c,若26120cbB,,,则a等于()A.6B.2C.3D.2答案D4.(2007重庆)在ABC△中,3AB,45A,75C,则BC( )A.33B.2C.2D.33答案A5.(2007山东)在直角ABC中,CD是斜边AB上的高,则下列等式不成立的是( )A.2ACACABB.2BCBABCC.2ABACCDD.22()()ACABBABCCDAB答案C6.(2006年全卷I)的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,则cosB=()A.41B.43C.42D.32答案B二、填空题7.(2005福建)在△ABC中,∠A=90°,kACkAB则),3,2(),1,(的值是.答案238.(2008浙江)在△ABC中,角A、B、C所对的边分别为a、b、c,若CaAcbcoscos3,则Acos_________.答案339.(2008湖北)在△ABC中,三个角,,ABC的对边边长分别为3,4,6abc,则coscoscosbcAcaBabC的值为.答案61210.(2007北京)在ABC△中,若1tan3A,150C,1BC,则AB.ABC答案21011.(2007湖南)在ABC△中,角ABC,,所对的边分别为abc,,,若1a,b=7,3c,则B.答案6512.(2007重庆)在△ABC中,AB=1,BC=2,B=60°,则AC=.答案3三、解答题14.(2008湖南)在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45且与点A相距402海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45+(其中sin=2626,090)且与点A相距1013海里的位置C.(I)求该船的行驶速度(单位:海里/小时);(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.解(I)如图,AB=402,AC=1013,26,sin.26BAC由于090,所以cos=2265261().2626由余弦定理得BC=.510cos222ACABACAB所以船的行驶速度为10515523(海里/小时).(II)解法一如图所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是B(x1,y2),C(x1,y2),BC与x轴的交点为D.由题设有,x1=y1=22AB=40,x2=ACcos1013cos(45)30CAD,y2=ACsin1013sin(45)20.CAD所以过点B、C的直线l的斜率k=20210,直线l的方程为y=2x-40.又点E(0,-55)到直线l的距离d=|05540|357.14所以船会进入警戒水域.解法二如图所示,设直线AE与BC的延长线相交于点Q.在△ABC中,由余弦定理得,222cos2ABBCACABCABBC=22240210510132402105=31010.从而2910sin1cos1.1010ABCABC在ABQ中,由正弦定理得,AQ=10402sin1040.sin(45)2210210ABABCABC由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EPBC于点P,则EP为点E到直线BC的距离.在RtQPE中,PE=QE·sinsinsin(45)PQEQEAQCQEABC=515357.5所以船会进入警戒水域.14.(2007宁夏,海南)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得BCDBDCCDs,,,并在点C测得塔顶A的仰角为,求塔高AB.解在BCD△中,πCBD.由正弦定理得sinsinBCCDBDCCBD.所以sinsinsinsin()CDBDCsBCCBD·.在Rt△ABC中,tansintansin()sABBCACB·.15.(2007福建)在ABC△中,1tan4A,3tan5B.(Ⅰ)求角C的大小;(Ⅱ)若ABC△最大边的边长为17,求最小边的边长.解(Ⅰ)π()CAB,1345tantan()113145CAB.又0πC,3π4C.(Ⅱ)34C,AB边最大,即17AB.又∵tanA<tanB,A、B2,0角A最小,BC边为最小边.由22sin1tancos4sincos1AAAAA,,且π02A,,得17sin17A.由sinsinABBCCA得:BC=AB·2sinsinCA.16.(2007浙江)已知ABC△的周长为21,且sinsin2sinABC.(I)求边AB的长;(II)若ABC△的面积为1sin6C,求角C的度数.解(I)由题意及正弦定理,得21ABBCAC,2BCACAB,两式相减,得1AB.(II)由ABC△的面积,sin61sin21CCACBC,得31ACBC,由余弦定理,得cosC=BCACABBCAC2222=2122)(22BCACABBCACBCAC,所以60C.17.(2007山东)20(本小题满分12分)如图,甲船以每小时302海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于1A处时,乙船位于甲船的北偏西105的方向1B处,此时两船相距20海里.当甲船航行20分钟到达2A处时,乙船航行到甲船的北偏西120方向的2B处,此时两船相距102海里,问乙船每小时航行多少海里?解方法一如图所示,连结A1B2,由已知A2B2=102,A1A2=2106020230,∴A1A2=A2B2,又∠A1A2B2=180°-120°=60°∴△A1A2B2是等边三角形,∴A1B2=A1A2=102.由已知,A1B1=20,∠B1A1B2=105°-60°=45°,在△A1B2B1中,由余弦定理,221BB=121BB+221BB-121BB·A1B2·cos45°=202+(102)2-2×20×102×22=200.∴B1B2=102.因此,乙船的速度的大小为20210×60=230(海里/小时).答乙船每小时航行230海里.19.(2007全国Ⅰ)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,2sinabA.(Ⅰ)求B的大小;(Ⅱ)若33a,5c,求b.解:(Ⅰ)由2sinabA,根据正弦定理得sin2sinsinABA,所以1sin2B,由ABC△为锐角三角形得π6B.(Ⅱ)根据余弦定理,得2222cosbacacB2725457.所以,7b20.(2007全国Ⅱ)在ABC△中,已知内角A,边23BC.设内角Bx,周长为y.(1)求函数()yfx的解析式和定义域;(2)求y的最大值.解:(1)ABC△的内角和ABC,由00ABC,,得20B.应用正弦定理,知23sinsin4sinsinsinBCACBxxA,2sin4sinsinBCABCxA.因为yABBCAC,所以224sin4sin2303yxxx,(2)因为14sincossin232yxxx543sin23xx,所以,当x,即x时,y取得最大值63第二部分四年联考题汇编2010年联考题题组二(5月份更新)1.(马鞍山学业水平测试)△AOB是边长为1的等边三角形,O是原点,ABx轴,以O为顶点,且过A,B的抛物线的方程是A.236yxB.236yxC.236yxD.233yx答案B2.设点O在ABC内部,且40OAOBOC,则ABC的面积与OBC的面积之比是A.2:1B.3:1C.4:3D.3:2答案:D3.(祥云一中三次月考理)已知边长为1的正三角形ABC中,则BCABABCACABC的值为A.21B.23C.21D.23答案:B4.ABC的三内角A,B,C所对边长分别是cba,,,设向量),sin,(Cbam)sinsin,3(ABcan,若nm//,则角B的大小为_____________答案655.(哈师大附中、东北师大附中、辽宁省实验中学)(1)由“若,,abcR则()()abcabc”类比“若a,b,c为三个向量则((ab)c=abc)”(2)在数列na中,110,22nnaaa猜想22nna(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”(4)已知8280128(2)xaaxaxax,则128256aaa.上述四个推理中,得出的结论正确的是____.(写出所有正确结论的序号)答案(2)(3)6.(哈师大附中、东北师大附中、辽宁省实验中学)设ABC的内角CBA,,所对的边分别为,,,cba且bcCa21cos.(1)求角A的大小;(2)若1a,求ABC的周长l的取值范围.解:(1)由bcCa21cos得1sincossinsin2ACCB…………2又sinsinsincoscossinBACACAC…………41sincossin2CAC,0sinC,21cosA,又0A3A…………6(2)由正弦定理得:BABabsin32sinsin,Ccsin32221sinsin1sinsin33labcBCBAB………83112sincos22BB6sin21B…………10,3A20,,3B65,66B1sin,162B故ABC的周长l的取值范围为2,3.…………12(2)另解:周长l1abcbc由(1)及余弦定理2222cosabcbcA221bcbc…………822()1313()2bcbcbc2bc…………10又12bcalabc即ABC的周长l的取值范围为2,3.…………127.(肥城市第二次联考)(本小题满分12分)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为075,030,于水面C处测得B点和D点的仰角均为060,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,21.414,62.449)解:在△ABC中,∠DAC=30°,∠ADC=60°-∠DAC=30,所以CD=AC=0.1又∠BCD=180°-60°-60°=60°,故CB是△CAD底边AD的中垂线,所以BD=BA,……5分在△ABC中,,ABCsinCBCAsinAAB即AB=,2062315sinACsin60因此,BD=。km33.020623故B,D的距离约为0.33km。……12分8.(池州市七校元旦调研)在ABC中,内角A、B、C的对边长分别为a、b、c,已知222acb,且sincos3cossin,ACAC求b分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1)222acb左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)sincos3cossin,ACAC过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.解法一:在ABC中sincos3cossin,ACAC则由正弦定理及余弦定理有:2222223,22abcbcaacabbc化简并整理得:2222()acb.又由已知222acb24bb.解得40(bb或舍).解法二:由余弦定理得:2222cosacbbcA.又222acb,0b。所以2cos2bcA…………………………………①又sincos3cossinACAC,sincoscossin4cossinACACACsin()4cossinACAC,即sin4cossinBAC由正弦定理得sinsinbBCc,故4cosbcA………………………②由①,②解得4b。题组一(1月份更新)一、选择题1、(2009青岛一模)已知点F、A分别为双曲线C:22221xyab(0,0)ab的左焦点、右顶点,点(0,)Bb满足0FBAB,则双曲线的离心率为A.2B.3C.132 D.152答案D2、(2009上海十四校联考)已知非零向量,21||||,0||||ACACABABBCACACABABACAB且满足与则△ABC的形状是()A.三边均不相等的三角形B.直角三角形C.等腰(非等边)三角形D.等边三角形答案D3、(2009枣庄一模)已知ABCcba分别为,,的三个内角A,B,C的对边,向量ABCbanmCCnCm则且若,10,).1cos,(cos),2,1cos2(周长的最小值为()A.3510B.3510C.3210D.3210答案B4、(2009上海奉贤区模拟考)在正方体1111-DCBAABCD中,点E在A1C1上,11141CAEA且ADzAByAAxAE1,则―――――――()。(A)2121,1zyx,,(B)211,21zyx,,(C)2131,1zyx,,(D)4141,1zyx,.答案D二、填空题5、(2009深圳一模)已知AD是ABC的中线,),(RACABAD,那么;若120A,2ABAC,则AD的最小值是.答案1三、解答题6、(2009湛江一模)已知向量)3,cos2(2xa,)2sin,1(xb,函数baxf)(,2)(bxg.(Ⅰ)求函数)(xg的最小正周期;(Ⅱ)在ABC中,cba,,分别是角CBA,,的对边,且3)(Cf,1c,32ab,且ba,求ba,的值.解:(Ⅰ)234cos2124cos112sin1)(22xxxbxg---------2分∴函数)(xg的最小周期242T----------4分(Ⅱ)xxxxbaxf2sin3cos2)2sin,1()3,cos2()(221)62sin(22sin312cosxxx-------------6分ED1CABC1A1BD1第4题31)62sin(2)(CCf1)62sin(C------------7分C是三角形内角∴)613,6(62C,∴262C即:6C-------------8分∴232cos222abcabC即:722ba----------------10分将32ab可得:71222aa解之得:432或a∴23或a32或bba∴2a3b------------12分7、(2009杭州高中第六次月考)已知A,B,C三点的坐标分别是A(3,0),B(0,3),C(cosθ,sinθ),其中2<θ<32,且BCAC.(1)求角θ的值;(2)当0≤x≤2时,求函数的最大值和最小值.解:(1)AC=(cosθ-3,sinθ),BC=(cosθ,sinθ-3)2分∵BCAC∴2222)3(sincossin)3(cos化简得:sinθ=cosθ5分∵2<θ<23∴θ=457分(2)当0≤x≤2时,45≤2x+θ≤4910分∴-1≤sin(2x+θ)≤22∴f(x)max=2f(x)min=-214分8、(2009杭州学军中学第七次月考)已知向量(sin,cos)mAA,(3,1)n,1mn,且A为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数()3cos24cossincos(0,)2fxxAxxx的值域.2sin2fxx解:(1)3sincos1,2sin()161sin(),623AAAAA(2)()3cos24cossincos33cos2sin22sin(2)3fxxxxxxx423333sin(2)12332xxy9、(2009嘉兴一中一模)已知ABC的三内角A,B,C所对边的长分别为a,b,c,设向量),3(babcm,),33(cban,nm//.(1)求Acos的值;(2)求)302sin(A的值.解:(1)因为nm//,所以cbababc333,得bccba31222…………3分又因为612cos222bcacbA…………………………………3分(2)由61cosA及),0(A,得635sinA,…………………………………2分所以1835cossin22sinAAA,…………………………………2分18171cos22cos2AA,…………………………………2分36171052cos212sin23)302sin(AAA………………………………2分10、(2009桐庐中学下学期第一次月考)已知A、B、C三点的坐标分别为)0,3(A、)3,0(B、).23,2(),sin,(cosC(1)若求角|,|||BCAC的值;(2)若.tan12sinsin2,12的值求BCAC解:(1))3sin,(cos),sin,3(cosBCAC,,45),23,2(,cossin||||,sin610||,cos610sin)3(cos||22又得由BCACBCAC(2)由,1)3(sinsincos)3(cos,1得BCAC.95tan12sinsin2,,95cossin2cossin1cossin2sin2tan12sinsin2,95cossin232cossin222所以又2009年联考题一、选择题1.(2009岳阳一中第四次月考).已知△ABC中,ABa,ACb,0ab,154ABCS,3,5ab,则BAC()A..30B.150C.0150D.30或0150答案C2.(2009河北区一模)在ABC中,||3.||4,||5,BCABAC则ACBC()A.-9B.0C.9D.15答案C3.(辽宁省沈阳二中2008—2009学年上学期高三期中考试)已知a,b,c为△ABC的三内角A,B,C的对边,向量)sin,(cos),1,3(AAnm,若nm,且BACcAbBa,,sincoscos则角的大小分别为()A.3,6B.6,32C.6,3D.3,3答案C二、填空题4.(2009长郡中学第六次月考)△ABC的三内角,,ABC所对边的长分别为,,abc设向量(,)pacb,(,)qbaca,若//pq,则角C的大小为答案3三、解答题5.(2009宜春)已知向量)sin,(sinBAm,)cos,(cosABn,Cnm2sin,且A、B、C分别为ABC的三边a、b、c所对的角。(1)求角C的大小;(2)若Asin,Csin,Bsin成等差数列,且18)(ACABCA,求c边的长。解:(1))sin(cossincossinBAABBAnm对于CBACCBAABCsin)sin(0,,,.sinCnm又Cnm2sin,.3,21cos,sin2sinCCCC(2)由BACBCAsinsinsin2,sin,sin,sin得成等差比数列,由正弦定理得.2bac18,18)(CBCAACABCA,即.36,18cosabCab由余弦弦定理abbaCabbac3)(cos22222,36,3634222ccc,.6c6.(辽宁省沈阳二中2008—2009学年上学期高三期中考试)在△ABC中,设A、B、C的对边分别为a、b、c向量,2||),cos,sin2(),sin,(cosnmAAnAAm若(1)求角A的大小;(2)若ABCacb求且,2,24的面积.解(1))sincos,sincos2(AAAAnm)4sin(44)sin(cos)sincos2(||22AAAAAnm2||nm,0)4sin(A又A0,4344A4,04AA(2)4,2Aac,2sinsinACacCC0,1sin又2CABC为等腰三角形,16)24(212ABCS7.(2009东北育才、天津耀华、大连育明、哈三中联考)在锐角ABC中,已知内角A、B、C所对的边分别为a、b、c,向量2(2sin(),3),cos2,2cos12BmACnB,且向量m,n共线。(1)求角B的大小;(Ⅱ)如果1b,求ABC的面积ABCS的最大值。解:(1)由向量,mn共线有:22sin()2cos13cos2,2BACB即tan23B,2分又02B,所以02B,则2B=3,即6B4分(Ⅱ)由余弦定理得2222cos,bacacB则2213(23)acacac,所以23,ac当且仅当ac时等号成立9分所以11sin(23)24ABCSacB。10分8.(广东省广州市2009年模拟)已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2,cosB=35.(1)若b=4,求sinA的值;(2)若△ABC的面积S△ABC=4,求b,c的值.解:(1)∵cosB=35>0,且01,∴t=1时,mn取最大值.依题意得,-2+4k+1=5,∴k=235.在△ABC中,角A、B、C的对边分别为a、b、c,若).(RkkBCBAACAB(Ⅰ)判断△ABC的形状;(Ⅱ)若kc求,2的值.解:(I)BcaBCBAAcbACABcos,cosBacAbcBCBAACABcoscos又BAABcossincossin即0cossincossinABBA0)sin(BABABAABC为等腰三角形.(II)由(I)知ba22cos2222cbcacbbcAbcACAB2c1k2007展开内容










 2022-2023学年江西省南昌市西湖区名校联盟七年级(下册)期中数学试卷word
2022-2023学年江西省南昌市西湖区名校联盟七年级(下册)期中数学试卷word 2020年高考真题数学(文科)(全国卷Ⅰ)+答案解析
2020年高考真题数学(文科)(全国卷Ⅰ)+答案解析 2017年北京高考数学(理科)试题试卷+答案(word版)
2017年北京高考数学(理科)试题试卷+答案(word版)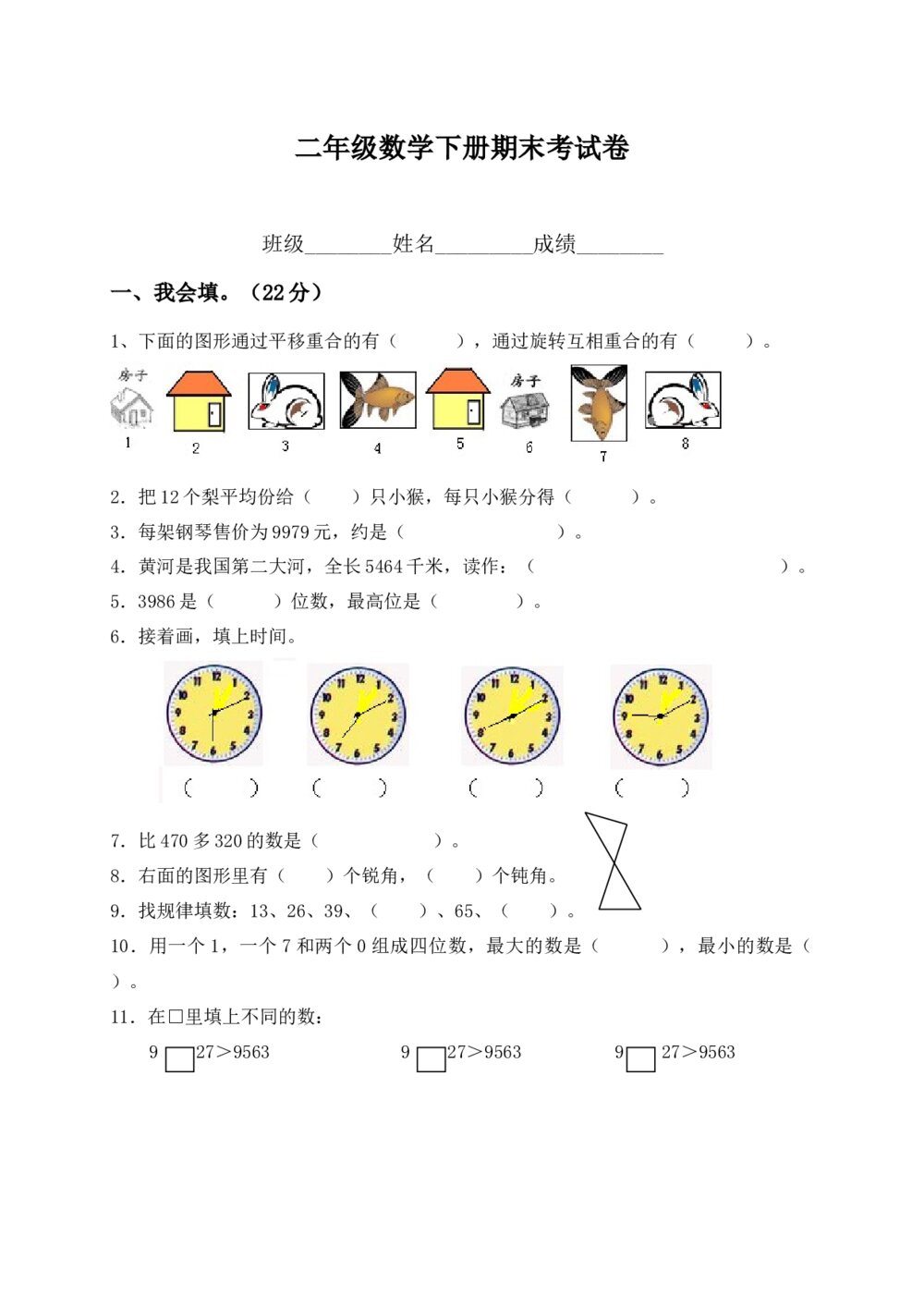 二年级数学下册期末考试卷word版
二年级数学下册期末考试卷word版 2011浙江省高考理科综合能力测试卷
2011浙江省高考理科综合能力测试卷 2013年北京高考(文科)数学试题试卷+答案
2013年北京高考(文科)数学试题试卷+答案