



《2011年高考一轮课时训练(理)8.3平面向量的数量积+参考答案(通用版)》是由用户上传到老师板报网,本为文库资料,大小为99.5 KB,总共有4页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 4页
- 99.5 KB
- VIP模板
- doc
- 数字产品不支持退货
第三节 平面向量的数量积题号12345答案一、选择题1.(2009年全国卷)已知向量a=(2,1),a·b=10,|a+b|=5,则|b|=( )A. B.C.5D.252.(2010年宁夏海南卷)已知a=(-3,2),b=(-1,0),向量λa+b与a-2b垂直,则实数λ的值为()A.-B.C.-D.3.(2010年东城统测)已知向量a,b满足|a|=2,|b|=3,|2a+b|=,则a与b的夹角为( )A.30°B.45°C.60°D.90°4.(2010年广东省实验中学月考)设a,b是非零向量,若函数f(x)=(xa+b)·(a-xb)的图象是一条直线,则必有( )A.a⊥bB.a∥bC.|a|=|b|D.|a|≠|b|5.在△ABC中,已知向量AB与AC满足·BC=0且·=,则△ABC为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形二、填空题6.(2010年江苏卷)已知向量a和向量b的夹角为30°,|a|=2,|b|=,则向量a和向量b的数量积a·b=________.7.(2010年江西卷)已知向量a=(3,1),b=(1,3),c=(k,2),若(a-c)⊥b则k=________.8.若向量a、b的夹角为150°,=,=4,则=__________.三、解答题9.(2010年福州模拟)已知向量a=,b=,且x∈,(1)求a·b及|a+b|;(2)若f(x)=a·b-2λ|a+b|的最小值是-,求λ的值.10.(2010年博兴月考)已知a=,b=,其中0<α<β<π.(1)求证:a+b与a-b互相垂直;(2)若ka+b与ka-b(k≠0)的长度相等,求β-α.参考答案1.解析:由|a+b|=5知(a+b)2=a2+b2+2ab=50,得|b|=5,选C.答案:C2.解析:向量λa+b=(-3λ-1,2λ),a-2b=(-1,2),因为两个向量垂直,故有(-3λ-1,2λ)·(-1,2)=0,即3λ+1+4λ=0,解得:λ=-,故选A.答案:A3.C4.解析:f(x)=(xa+b)·(a-xb)=-a·bx2+(|a|2-|b|2)x+a·b,若函数f(x)的图象是一条直线,即其二次项系数为0,∴a·b=0⇒a⊥b.答案:A5.解析:非零向量AB与AC满足·BC=0,即角A的平分线垂直于BC,∴AB=AC,又cosA=·=,∴∠A=,所以△ABC为等边三角形,选D.答案:D6.解析:a×b=2××=3.答案:37.解析:因为a-c=(3-k,-1),且(a-c)⊥b,∴(3-k)×1+(-1)×3=0所以k=0.答案:08.解析:====2.答案:29.解析:(1)a·b=cosx·cos-sinx·sin=cos2x,|a+b|===2.∵x∈,∴cosx>0,∴|a+b|=2cosx.(2)f(x)=cos2x-4λcosx,即f(x)=2(cosx-λ)2-1-2λ2,∵x∈,∴0≤cosx≤1.①当λ<0时,当且仅当cosx=0时,f(x)取得最小值-1,这与已知矛盾;②当0≤λ≤1时,当且仅当cosx=λ时,f(x)取得最小值-1-2λ2,由已知得-1-2λ2=-,解得λ=;③当λ>1时,当且仅当cosx=1时,f(x)取得最小值1-4λ,由已知得1-4λ=-,解得λ=,这与λ>1相矛盾,综上所述,λ=为所求.10.解析:(1)证明:∵(a+b)·(a-b)=a2-a·b+b·a-b2=a2-b2=|a|2-|b|2=-=1-1=0,所以a+b与a-b互相垂直.(2)ka+b=,ka-b=,所以|ka+b|=,|ka-b|=,因为|ka+b|=|ka-b|,所以k2+2kcos+1=k2-2kcos+1,有2kcos=-2kcos,因为k≠0,故cos=0,又因为0<α<β<π,0<β-α<π,所以β-α=.展开内容




 2012山东卷高考文科数学+参考答案
2012山东卷高考文科数学+参考答案 2017年高考数学知识方法专题9《系列4选讲第41练 坐标系与参数方程》
2017年高考数学知识方法专题9《系列4选讲第41练 坐标系与参数方程》 人教版小学数学六年级上期末阶段检测(4)+参考答案
人教版小学数学六年级上期末阶段检测(4)+参考答案 高考试题(山东卷)——文科数学+(答案解析)
高考试题(山东卷)——文科数学+(答案解析) 山东省高考数学仿真模拟试题+参考答案
山东省高考数学仿真模拟试题+参考答案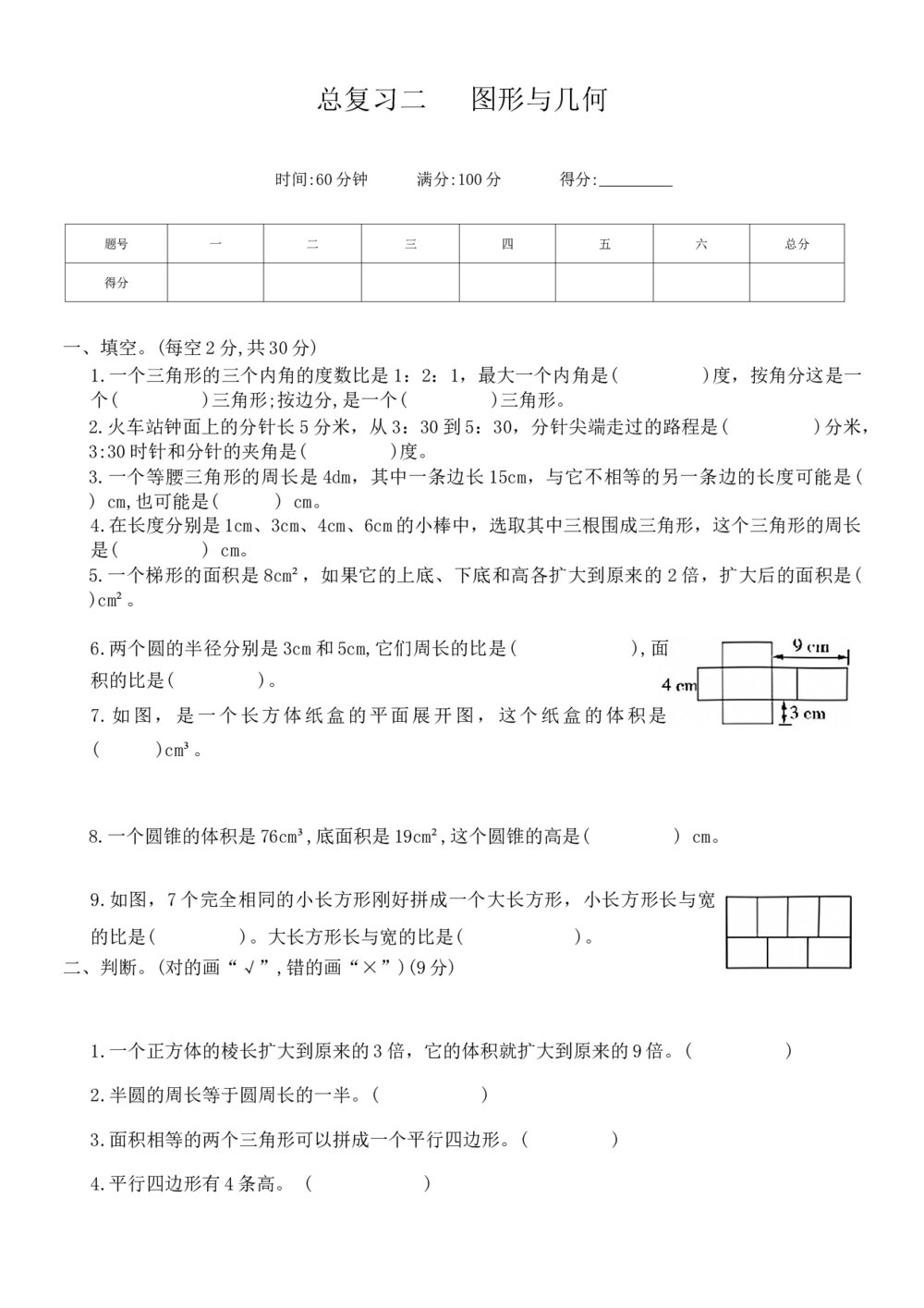 北师大版六年级数学下册 总复习二《图形与几何》word版无答案
北师大版六年级数学下册 总复习二《图形与几何》word版无答案