









试读已结束,还剩3页未读,您可下载完整版后进行离线阅读
《2011年石家庄市高中毕业班第一次模拟(文科)数学试卷+答案》是由用户上传到老师板报网,本为文库资料,大小为661.5 KB,总共有13页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 13页
- 661.5 KB
- VIP模板
- doc
- 数字产品不支持退货
试卷类型:A2011年石家庄市高中毕业班第一次模拟考试试卷数学(文科)说明:1.本试卷共4页,包括三道大题,22道小题,共150分.其中第一道大题为选择题.2.所有答案请在答题卡上作答,在本试卷和草稿纸上作答无效.答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题.3.做选择题时,如需改动,请用橡皮将原选答案擦干净,再选涂其他答案.参考公式:如果事件A、B互斥,那么P(A+B)=P(A)+P(B)如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率Pn(k)=Cknpk(1-p)kn(k=0,l,2,…,n)球的表面积公式S=4R2其中R表示球的半径球的体积公式V=34R3其中R表示球的半径一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中。只有一项是符合题目要求的.1.设M={9|xx},N={9|2xx},则A.MNB.NMC.MRCND.NRCM2.抛物线y2=4x的焦点坐标为A.(2,0)B.(1,0)C.(0,-4)D.(-2,0)新课标第一网3.已知直线012:1yaxl与直线0)3(:2ayxal,若1l2l,则实数a的值为A.1B.2C.6D.1或24.右图中的小网格由等大的小正方形拼成,则向量baA.213eeB.213eeC.213eeD.213ee5.已知),,0(且22cossin,则cossin的值为A.2B.26C.2D.266.已知椭圆162x+252y=1的焦点分别是1F、2F,P是椭圆上一点,若连结1F、2F、P三点恰好能构成直角三角形,则点P到y轴的距离是A.516B.3C.316D.3257.若多项式x10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,则a8的值为A.10B.45C.-9D.-458.设x,y满足约束条件0004402yxyxyx,若目标函数)0,0(babyaxz的最大值为6,则a1+b2的最小值为A.1B.3C.2D.49.用直线y=m和直线y=x将区域x2+y26分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是A.)3,3(B.)2,3(C.)2,2(D.)3,2(10.对于非空数集A,若实数M满足对任意的Aa恒有M,a则M为A的上界;若A的所有上界中存在最小值,则称此最小值为A的上确界,那么下列函数的值域中具有上确界的是A.y=2xB.y=x)21(C.y=x21D.y=xln11.已知数列{an}满足{an}=.8,,8,2)31(7nannan若对于任意的*Nn都有ana1n,则实数a的取值范围是A.(0,31)B.(0,21)C.(31,21)D.(21,1)12.在直三棱柱ABC—A1B1C1中,FDAAACABBAC和,1,21分别为棱AC、AB上的动点(不包括端点),若FC1,1DB则线段DF长度的取值范围为A.]23,22[B.)1,33[C.)1,22[D.]22,32[二、填空题:本大题共4小题,每小题5分;共20分.13.不等式031xx的解集为.14.在三棱锥P-ABC中,PBABC,90平面ABC,AB=BC=22,PB=2,则点B到平面PAC的距离是.15.已知a、b、c成等差数列,则直线0cbyax被曲线02222yxyx截得的弦长的最小值为.16.在ABC中,AB=2AC=2,AB·AC=-1,若ACABAOxx21(O是ABC的外心),则21xx的值为.三、解答题:本大题共6小题,共70分.解答应写出文宇说明,证明过程或演算步骤.17.(本小题满分l0分)在ABC中,角A、B、C的对边长分别是a、b、c,若.0cos)2(cosBcaCb(I)求内角B的大小;(Ⅱ)若b=2,求ABC面积的最大值.18.(本小题满分12分)已知各项都不相等的等差数列{na}的前6项和为60,且6a为1a和21a的等比中项.(I)求数列na的通项公式;(Ⅱ)若数列{nb}满足,1Nnabbnnn且31b,求数列{nb1}的前n项和nT.19.(本小题满分12分)如图所示,五面体ABCDE中,正ABC的边长为1,AE平面ABC,CD∥AE,且CD=21AE.(I)设CE与平面ABE所成的角为,AE=),0(kk若],4,6[求k的取值范围;(Ⅱ)在(I)和条件下,当k取得最大值时,求平面BDE与平面ABC所成角的大小.20.(本小题满分l2分)在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分已知某选手回答A、B、C三道题正确的概率分别为21、31、41,且回答各题时相互之间没有影响.(I)若此选手按A、B、C的顺序答题,求其必答题总分不小于80分的概率;(Ⅱ)若此选手可以自由选择答题顺序,求其必答题总分为50分的概率.21.(本小题满分12分)已知函数)(241)(24Raxaxxxf.(I)若23a,求函数)(xf极值;(II)设F(x)=2)12()(22\'xaxaxf,若函数F(x)在[0,1]上单调递增,求a的取值范围.22.(本小题满分l2分)已知椭圆1322yx的上、下顶点分别为),(),(,11121yxNyxMAA和和是椭圆上两个不同的动点.(I)求直线MA1与NA2交点的轨迹C的方程;(Ⅱ)若过点F(0,2)的动直线z与曲线C交于A、B两点,,FBAF问在y轴上是否存在定点E,使得)(EBEAOF?若存在,求出E点的坐标;若不存在,说明理由.2010-2011年度石家庄市第一次模拟考试文科数学答案一、选择题:本大题共12个小题,每小题5分,共60分.(A卷答案):1-5BBDDD6-10ABBAB11-12DC(B卷答案):1-5AADDD6-10BAABA11-12DC二、填空题:本大题共4个小题,每小题5分,共20分.13.|31xx14.215.216.136三、解答题:本大题共6小题,共70分.解答应写文字说明,证明过程或演算步骤.17.(本小题满分10分)解:(I)解法一:∵0cos)2(cosBcaCb,由正弦定理得:BABCCBcossin2cossincossin,即BACBcossin2)sin(.………………2分在ABC△中,ACBπ,∴BAAcossin2sin,0sinA………………3分∴21cosB,∴3π2B.………………5分E解法二:因为0cos)2(cosBcaCb,由余弦定理222222(2)022abcacbbacabac,化简得222aaccb,……………2分又余弦定理2222cosacacBb,……………3分所以1cos2B,又(0,)B,有23B.……………5分(II)解法一:∵2222cosbacacB,∴224acac,……………6分23acacac.∴43ac,………………8分∴11433sin22323ABCSacB.………………9分当且仅当233ac时取得等号.……………………10分解法二:由正弦定理知:BbCcsinsin,)3πsin(3343π2sin)3πsin(2sinsinAABCbc.………………6分∴ABCS△Abcsin21)3π0(sin)3πsin(334AAA,AAAsin)sin21cos23(334AAA2sin332cossin2)2cos1(332sinAA332cos332sinAA33)6π2sin(332A,………………8分∵3π0A,∴6π56π26πA,∴12πsin)6π2sin(A,………………9分∴3333)6π2sin(332A,即ABC△的面积ABCS△的最大值是33.………………10分18.(本小题满分12分)解:(Ⅰ)设等差数列na的公差为d(0d),则1211161560,205,adaadad………………2分解得12,5,da…………………4分∴23nan.………………5分(Ⅱ)由1nnnbba,∴11nnnbba*2,nnN,………………6分112211nnnnnbbbbbbbb1211nnaaab11432nnnn.∴2nbnn*nN.…………………8分∴11111222nbnnnn………………10分111111123242nTnn21311352212412nnnnnn.………………12分19.(本小题满分12分)解:方法一:(Ⅰ)取AB中点M,连结CM、EM,由ABC为正三角形,得CMAB,又AEABC面,则AECM,可知CMABE面,所以MEC为CE与平面ABE所成角.……………2分232tan14CMEMk,……………4分因为[,]64,得3tan[,1]3,得222k.……………6分(Ⅱ)延长ACED、交于点S,连BS,可知平面BDE平面ABC=BS.………………………7分由//CDAE,且12CDAE,又因为ACCSBC=1,从而ABBS,…………………8分又AE面ABC,由三垂线定理可知BEBS,即EBA为平面BDE与平面ABC所成的角;……………………10分则tan2AEEBAAB,从而平面BDE与面ABC所成的角的大小为arctan2.………………12分方法二:解:(Ⅰ)如图以C为坐标原点,CA、CD为y、z轴,垂直于CA、CD的直线CT为x轴,建立空间直角坐标系(如图),则设(0,1,0)A,(0,0,)2kD,(0,1,)Ek,31(,,0)22B.……………2分取AB的中点M,则33(,,0)44M,易知,ABE的一个法向量为33(,,0)44CM,由题意22334sin||||392111616CECMCECMkk.………………4分由[,]64,则12232sin221k,得222k.…………………6分(Ⅱ)由(Ⅰ)知k最大值为2,则当2k时,设平面BDE法向量为x,y,z)n=(,则20,2320.222DEyzyBExznn取n=(-3,-1,2),………………8分又平面ABC法向量为m=(0,0,1),……………………10分所以cos(,)nm=233231,所以平面BDE与平面ABC所成角大小3arccos.3……………………12分20.(本小题满分12分)解:(I)若考生按A,B,C的顺序答题,记该生最后得分不小于80分为事件E.………………1分.新课标第一网则111()234PE…………………2分1111(1)23412,……………………4分所以若此选手按A、B、C的顺序答题,求其必答题总分不小于80分的概率.…………………5分(II)考生自由选择答题顺序,记总分得50分为事件D,记D1表示A,B答对,C答错,D2表示A,B答错,C答对,则D=D1+D2,且D1,D2互斥.………………6分又81)411(3121)(1DP,………………8分36141)311(21)(33222AADP.…………………10分所以7211)()()()(2121DPDPDDPDP.………………12分21.(本小题满分12分)(Ⅰ)解:当32a时,2332120fxxxxx解得:1x或2x.………………2分∵当,2x时,0fx;当2,1x时,0fx;当1,x时,0fx.……………………4分∴fx的极小值为26f.…………………5分(Ⅱ)解法一:322212Fxxaxaax,即2234220,Fxxaxaa在0,1上恒成立,……………7分即2221(1)3().33aaFxx(1)当对称轴12(0,1)3ax时,只要2(103a),即a,…………………9分(2)当对称轴1213ax或1203ax时,只要(0)0;(1)0FF.即2220;32(21)0aaaaa-2.得1a或2a.…………………11分综上所述,1a或2a.………………12分解法二:322212Fxxaxaax,22342232Fxxaxaaxaxa.………………6分由已知得:320Fxxaxa在0,1上恒成立,………………8分新课标第一网当23aa时,即1a时,符合题意;………………9分当23aa时,即1a时,只须1a或203a,∴1a或2a,∴2a;……………………10分当23aa时,即1a时,只须0a或213a,∴0a或1a,∴1a.………………11分综上所述,1a或2a.…………………12分22.(本小题满分12分)解:(Ⅰ)方法一:设直线MA1与NA2的交点为),(yxP,∵21AA,是椭圆1322yx的上、下顶点,∴12(03)(03)AA,,,-…………………1分11133yAMyxx:,12133yANyxx:,两式相乘得22121233xxyy.………………………3分而),(11yxM在椭圆1322yx(10x)上,所以132121yx,即332121xy,所以2233xy.……………4分又当0x时,不合题意,去掉顶点.∴直线MA1与NA2的交点的轨迹C的方程是221(0)3yxx;……………5分方法二:设直线MA1与NA2的交点为),(yxP,∵21AA,是椭圆1322yx的上、下顶点,∴12(03)(03)AA,,,-…………………1分∵PMA、、1共线,PNA、、2共线,∴xyxy3311…………①xyxy3311…………②…………………3分①②得22212133xyxy,又∵132121yx即332121xy,∴3322xy,即221(0)3yxx,∴直线MA1与NA2的交点的轨迹C的方程是1322xy;(0x)……………5分(Ⅱ)假设存在满足条件的直线,由已知,其斜率一定存在,设其斜率为k,设)(11yxA,,)(22yxB,,)0(0yE,,由2221.3ykxyx,得)3(014)3(222kkxxk,3134221221kxxkkxx,.…………………6分11(2)AFxy,,22(2)FBxy,,∵AFFB,∴21xx,∵02x,∴21xx,∵(02)OF,,110()EAxyy,,220()EBxyy,,121020()EAEBxxyyyy,,,又∵()OFEAEB,∴()0OFEAEB,∴0)2(0020121yyyyxx(),即00201yyyy.………………………8分将211kxy,222kxy,21xx代入上式并整理得0212121)()(22yxxxxxkx,…………………9分当021xx时,2323432222221210kkkkxxxkxy,当021xx时,0k,0212121)()(22yxxxxxkx恒成立,…………………11分所以,在y轴上存在定点E,使得()OFEAEB,点E的坐标为)230(,.………12分










 二年级数学《表内除法(二)》考试卷及参考答案(word版)
二年级数学《表内除法(二)》考试卷及参考答案(word版) 莱州市2015高三期末数学(文科)试卷+答案
莱州市2015高三期末数学(文科)试卷+答案 丰台区2011年高三一模数学(理科)试题试卷+(含答案)
丰台区2011年高三一模数学(理科)试题试卷+(含答案)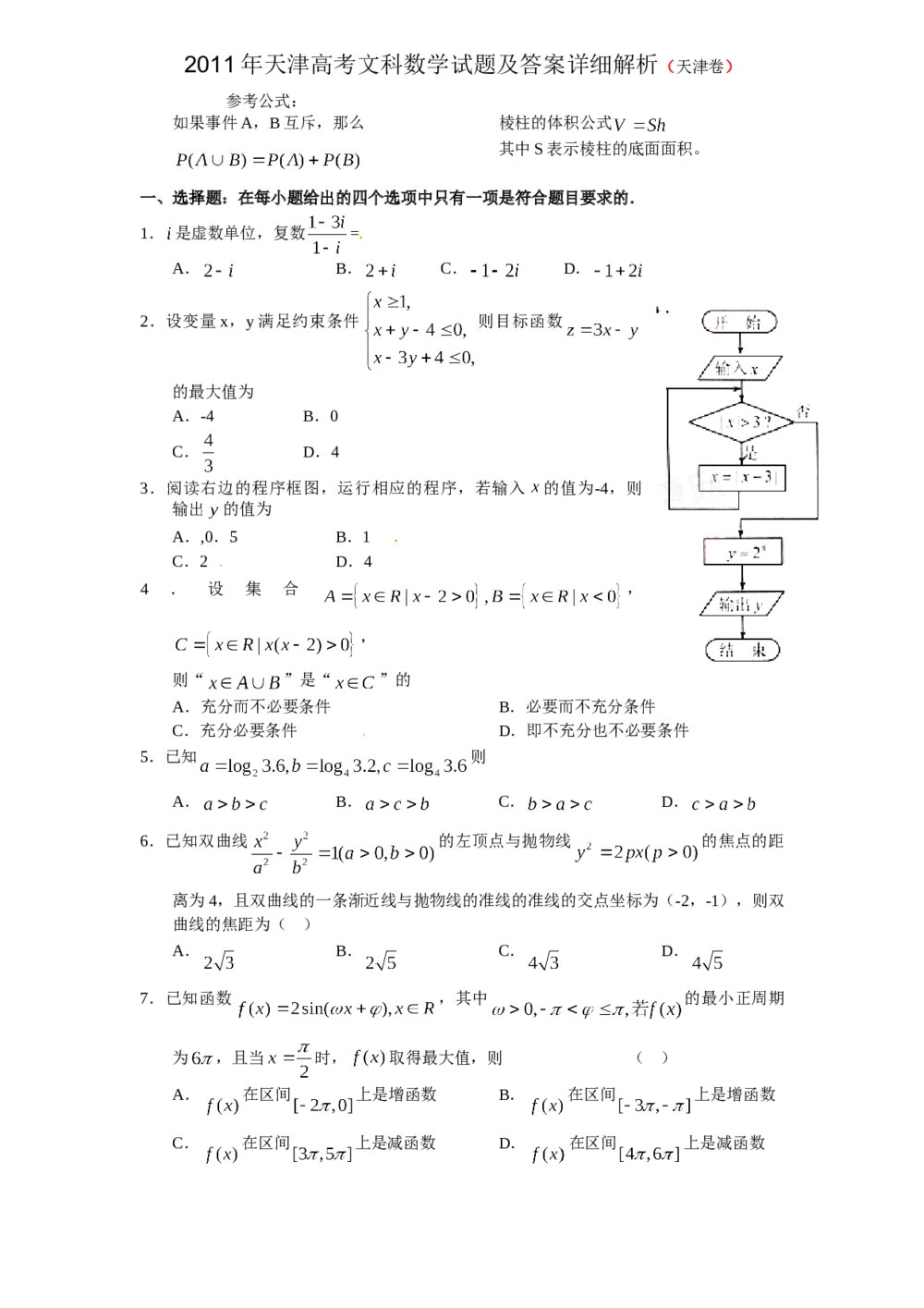 2011年天津高考(文科)数学试题及答案详细解析(Word版)
2011年天津高考(文科)数学试题及答案详细解析(Word版) 2012新课标文科数学回归教材《3导数》
2012新课标文科数学回归教材《3导数》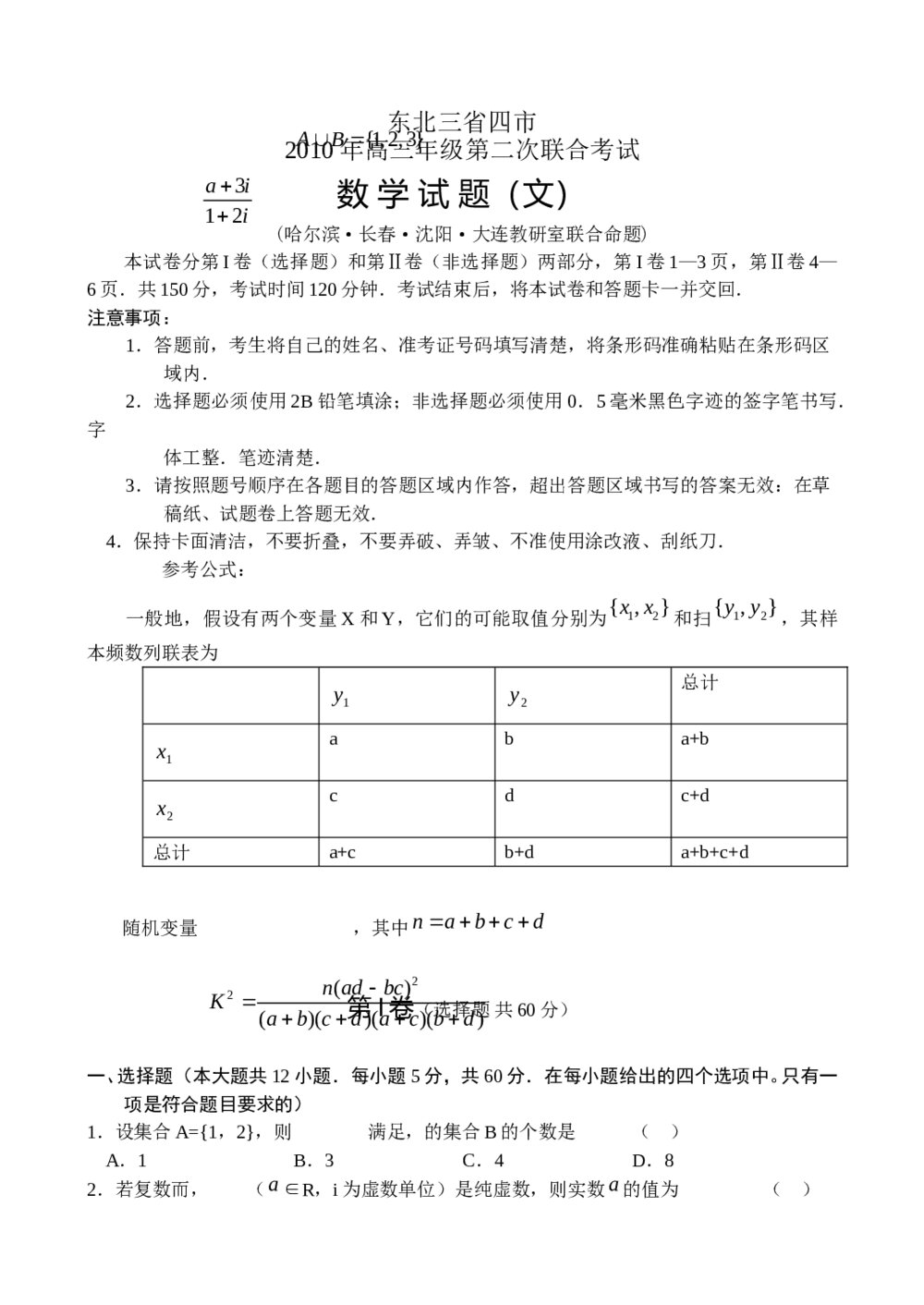 东北三省四市高三第二次联考试(数学文科)试题试卷+参考答案
东北三省四市高三第二次联考试(数学文科)试题试卷+参考答案