









试读已结束,还剩2页未读,您可下载完整版后进行离线阅读
《2011年天津高考(文科)数学试题及答案详细解析(Word版)》是由用户上传到老师板报网,本为文库资料,大小为1021 KB,总共有12页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 12页
- 1021 KB
- VIP模板
- doc
- 数字产品不支持退货
2011年天津高考文科数学试题及答案详细解析(天津卷)参考公式:如果事件A,B互斥,那么棱柱的体积公式其中S表示棱柱的底面面积。一、选择题:在每小题给出的四个选项中只有一项是符合题目要求的.1.是虚数单位,复数=A. B. C. D.2.设变量x,y满足约束条件则目标函数的最大值为A.-4 B.0C. D.43.阅读右边的程序框图,运行相应的程序,若输入的值为-4,则输出的值为A.,0.5B.1C.2D.44.设集合,,则“”是“”的A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.即不充分也不必要条件5.已知则A. B.C. D.6.已知双曲线的左顶点与抛物线的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的准线的交点坐标为(-2,-1),则双曲线的焦距为()A.B.C.D.7.已知函数,其中的最小正周期为,且当时,取得最大值,则()A.在区间上是增函数B.在区间上是增函数C.在区间上是减函数D.在区间上是减函数8.对实数,定义运算“”:设函数。若函数的图象与轴恰有两个公共点则实数的取值范围是()A.B.C.D.[-2,-1]二、填空题:本大题共6小题,每小题5分,共30分.9.已知集合为整数集,则集合中所有元素的和等于________10.一个几何体的三视图如图所示(单位:),则该几何体的体积为__________11.已知为等差数列,为其前项和,,若则的值为_______12.已知,则的最小值为__________13.如图已知圆中两条弦与相交于点,是延长线上一点,且若与圆相切,则的长为__________14.已知直角梯形中,//,,,是腰上的动点,则的最小值为____________三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.15.编号为的16名篮球运动员在某次训练比赛中的得分记录如下:运动员编号得分1535212825361834运动员编号得分1726253322123138(Ⅰ)将得分在对应区间内的人数填入相应的空格;区间人数(Ⅱ)从得分在区间内的运动员中随机抽取2人,(i)用运动员的编号列出所有可能的抽取结果;(ii)求这2人得分之和大于50的概率.16.在△中,内角的对边分别为,已知(Ⅰ)求的值;(Ⅱ)的值.17.(本小题满分13分)如图,在四棱锥中,底面为平行四边形,,,为中点,平面,,为中点.(Ⅰ)证明://平面;(Ⅱ)证明:平面;(Ⅲ)求直线与平面所成角的正切值.18.(本小题满分13分)设椭圆的左、右焦点分别为F1,F2。点满足(Ⅰ)求椭圆的离心率;(Ⅱ)设直线PF2与椭圆相交于A,B两点,若直线PF2与圆相交于M,N两点,且,求椭圆的方程。19.(本小题满分14分)已知函数,其中.(Ⅰ)当时,求曲线在点处的切线方程;(Ⅱ)当时,求的单调区间;DCABPMO(Ⅲ)证明:对任意的在区间内均存在零点.20.(本小题满分14分)已知数列满足(Ⅰ)求的值;(Ⅱ)设,证明是等比数列;(Ⅲ)设为的前项和,证明参考答案一、选择题:本题考查基本知识和基本运算,每小题5分,满分40分。1.【答案】A【解析】.2.【答案】D【解析】可行域如图:联立解得当目标直线移至(2.2)时,有最大值4.3.【答案】C【解析】当时,;当时,当时,,∴.4.【答案】C【解析】∵,,∴,或,又∵或,∴,即“”是“”的充分必要条件.5.【答案】B【解析】∵,又∵为单调递增函数,∴,∴.6.【答案】Bxyo1234-1-2-3-41234x=1x-3y+4=0x+y-4=0【解析】双曲线的渐近线为,由双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1)得,即,又∵,∴,将(-2,-1)代入得,∴,即.7.【答案】A【解析】∵,∴.又∵且,∴当时,,要使递增,须有,解之得,当时,,∴在上递增.8.【答案】B【解析】则的图象如图,∵函数的图象与轴恰有两个公共点,∴函数与的图象有两个交点,由图象可得.二、填空题:本题考查基本知识和基本运算,每小题5分,满分30分。9.【答案】3xyo1234-1-2-3-41234-1-2-3【解析】.∴,即10.【答案】4【解析】.11.【答案】110【解析】设等差数列的首项为,公差为,由题意得,,解之得,∴.12.【答案】18【解析】∵,∴,∴.13.【答案】【解析】设,,,由得,即.∴,由切割定理得,∴.14.【答案】5【解析】建立如图所示的坐标系,设,则,设则,∴.三、解答题(15)本小题主要考查用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式的等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力,满分13分。(Ⅰ)解:4,6,6ABCDoxy(Ⅱ)(i)解:得分在区间内的运动员编号为从中随机抽取2人,所有可能的抽取结果有:,,共15种。(ii)解:“从得分在区间内的运动员中随机抽取2人,这2人得分之和大于50”(记为事件B)的所有可能结果有:,共5种。所以(16)本小题主要考查余弦定理、两角和的余弦公式、同角三角函数的基本关系、二倍角的正弦、余弦公式等基础知识,考查基本运算能力,满分13分。(Ⅰ)解:由所以(Ⅱ)解:因为,所以所以(17)本小题主要考查直线与平面平行、直线与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力和推理论证能力。满分13分。(Ⅰ)证明:连接BD,MO,在平行四边形ABCD中,因为O为AC的中点,所以O为BD的中点,又M为PD的中点,所以PB//MO。因为平面ACM,平面ACM,所以PB//平面ACM。(Ⅱ)证明:因为,且AD=AC=1,所以,即,又PO平面ABCD,平面ABCD,所以,所以平面PAC。(Ⅲ)解:取DO中点N,连接MN,AN,因为M为PD的中点,所以MN//PO,且平面ABCD,得平面ABCD,所以是直线AM与平面ABCD所成的角,在RtDAO中,11,2ADAO,所以52DO,从而,在,即直线AM与平面ABCD所成角的正切值为(18)本小题主要考查椭圆的标准方程和几何性质、直线的方程、两点间的距离公式、点到直线的距离公式、直线与圆的位置关系等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的数学思想,考查解决问题能力与运算能力,满分13分。(Ⅰ)解:设,因为,所以,整理得(舍)或(Ⅱ)解:由(Ⅰ)知,可得椭圆方程为,直线FF2的方程为A,B两点的坐标满足方程组2223412,3().xycyxc消去并整理,得。解得,得方程组的解不妨设,,所以于是圆心到直线PF2的距离因为,所以整理得,得(舍),或所以椭圆方程为(19)本小题主要考查导数的几何意义、利用导数研究函数的单调性、曲线的切线方程、函数的零点、解不等式等基础知识,考查运算能力及分类讨论的思想方法,满分14分。(Ⅰ)解:当时,所以曲线在点处的切线方程为(Ⅱ)解:,令,解得因为,以下分两种情况讨论:(1)若变化时,的变化情况如下表:+-+所以,的单调递增区间是的单调递减区间是。(2)若,当变化时,的变化情况如下表:+-+所以,的单调递增区间是的单调递减区间是(Ⅲ)证明:由(Ⅱ)可知,当时,在内的单调递减,在内单调递增,以下分两种情况讨论:(1)当时,在(0,1)内单调递减,所以对任意在区间(0,1)内均存在零点。(2)当时,在内单调递减,在内单调递增,若所以内存在零点。若所以内存在零点。所以,对任意在区间(0,1)内均存在零点。综上,对任意在区间(0,1)内均存在零点。(20)本小题主要考查等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析能力和解决问题的能力及分类讨论的思想方法。满分14分。(Ⅰ)解:由,可得又,当当(Ⅱ)证明:对任意①②②-①,得所以是等比数列。(Ⅲ)证明:,由(Ⅱ)知,当时,故对任意由①得因此,于是,故展开内容










 2017年高考数学知识方法专题7《解析几何第35练 圆锥曲线中的探索性问题》
2017年高考数学知识方法专题7《解析几何第35练 圆锥曲线中的探索性问题》 高考文科数学二轮专题复习题《选修模块 专题1 第1讲 导数的简单应用》
高考文科数学二轮专题复习题《选修模块 专题1 第1讲 导数的简单应用》 2020年北京市高考(理科)数学试题试卷(原卷版)
2020年北京市高考(理科)数学试题试卷(原卷版)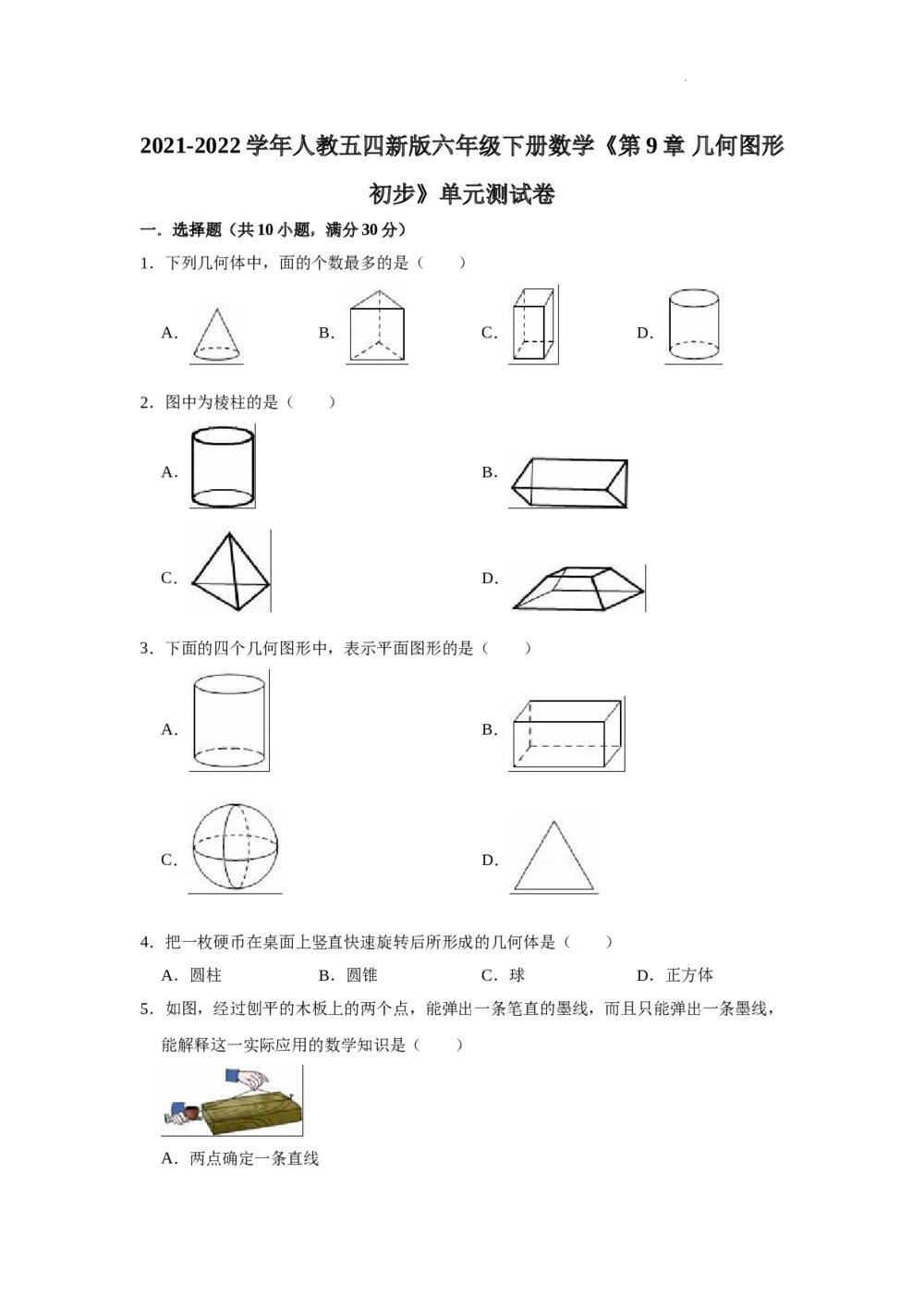 2021-2022学年人教版(五四制)六年级下册数学《第9章几何图形初步》单元测试卷+(含参考答案)
2021-2022学年人教版(五四制)六年级下册数学《第9章几何图形初步》单元测试卷+(含参考答案) 2010年高考数学试题分类汇编--数列+(答案解析)
2010年高考数学试题分类汇编--数列+(答案解析) 九年级数学检测试题试卷(word版)
九年级数学检测试题试卷(word版)