









试读已结束,还剩23页未读,您可下载完整版后进行离线阅读
《2012年江苏省高考数学一轮训练试题考点6《解析几何》》是由用户上传到老师板报网,本为文库资料,大小为2.21 MB,总共有33页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 33页
- 2.21 MB
- VIP模板
- doc
- 数字产品不支持退货
2010-2011学年度第一学期江苏省南通市六所省重点高中联考试卷数学Ⅰ试题2011.13、方程的曲线是焦点在y轴上的双曲线,则m的取值范围是▲答案:0m9、已知椭圆22221(0)yxabab的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则||||FAOH的最大值为▲13、设M1(0,0),M2(1,0),以M1为圆心,|M1M2|为半径作圆交x轴于点M3(不同于M2),记作⊙M1;以M2为圆心,|M2M3|为半径作圆交x轴于点M4(不同于M3),记作⊙M2;……;以Mn为圆心,|MnMn+1|为半径作圆交x轴于点Mn+2(不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:当n=1时,|A1B1|=2;当n=2时,|A2B2|=15;当n=3时,|A3B3|=23354213+-;当n=4时,|A4B4|=34354213--;……由以上论断推测一个一般的结论:对于n∈N*,|AnBn|=▲17、(本题满分15分)已知圆:C22(2)4xy,相互垂直的两条直线1l、2l都过点(,0)Aa.(Ⅰ)当2a时,若圆心为(1,)Mm的圆和圆C外切且与直线1l、2l都相切,求圆M的方程;(Ⅱ)当1a时,求1l、2l被圆C所截得弦长之和的最大值,并求此时直线1l的方程.解:(Ⅰ)设圆M的半径为r,易知圆心),1(mM到点)0,2(A的距离为r2,∴222222)2()21(2)21(rmrm……………………………………………………………4分解得2r且7m∴圆M的方程为4)7()1(22yx…………………7分(Ⅱ)当1a时,设圆C的圆心为C,1l、2l被圆C所截得弦的中点分别为FE,,弦长分别为21,dd因为四边形AECF是矩形,所以1222ACCFCE,即124242221dd,化简得…………………………10分从而1422222121dddd,等号成立1421dd,1421dd时,142)(max21dd,即1l、2l被圆C所截得弦长之和的最大值为142…………………………………13分此时141d,显然直线1l的斜率存在,设直线1l的方程为:)1(xky,则22)214(41kk,1k,∴直线1l的方程为:01yx或01yx…………………………15分江苏省2010高考数学模拟题(压题卷)8.已知F1、F2分别是椭圆12222byax,)0(ba的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A、B两点,若△F2AB是等边三角形,则椭圆的离心率等于13.三、解析几何题1.已知过点(1,0)A的动直线l与圆22:(3)4Cxy相交于,PQ两点,M是PQ中点,l与直线:360mxy相交于N.(1)求证:当l与m垂直时,l必过圆心C;(2)当23PQ时,求直线l的方程;(3)探索AMAN是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.解:(1)l与m垂直,且11,3,3mkk故直线l方程为3(1),yx即330.xy圆心坐标(0,3)满足直线l方程,当l与m垂直时,l必过圆心C.(2)①当直线l与x轴垂直时,易知1x符合题意.②当直线l与x轴不垂直时,设直线l的方程为(1),ykx即0kxyk,23,431PQCM,则由2311kCMk,得43k,直线:4340.lxy故直线l的方程为1x或4340.xy(3),().CMMNAMANACCMANACANCMANACAN①当l与x轴垂直时,易得5(1,),3N则5(0,),3AN又(1,3)AC,5AMANACAN.②当l的斜率存在时,设直线l的方程为(1),ykx则由(1),360,ykxxy得365(,),1313kkNkk则55(,).1313kANkk5155.1313kAMANACANkk综上所述,AMAN与直线l的斜率无关,且5AMAN.2.已知A、B是椭圆2214xy的左、右顶点,直线(22)xtt交椭圆于M、N两点,经过A、M、N的圆的圆心为1C,经过B、M、N的圆的圆心为2C.(1)求证12CC为定值;(2)求圆1C与圆2C的面积之和的取值范围.解:(1)由题设A(-2,0),B(2,0),由2214xtxy,,解出22(,1),(,1)44ttMtNt.设1122(,0),(,0)CxCx,由22112()14txtx解出13(2)8tx.同理,2222()14txxt解出23(2)8tx,122132CCxx(定值).(2)两圆半径分别为131028tx及210328tx,两圆面积和222(310)(103)(9100)6432Sttt,所以S的取值范围是257,84.3.已知圆221:(1)16Fxy,定点2(1,0),F动圆过点2F,且与圆1F相内切.(1)求点M的轨迹C的方程;(2)若过原点的直线l与(1)中的曲线C交于A,B两点,且1ABF的面积为32,求直线l的方程.解:(1)设圆M的半径为r,因为圆M与圆1F内切,所以2MFr,所以124MFMF,即124MFMF.所以点M的轨迹C是以12,FF为焦点的椭圆,设椭圆方程为22221(0)xyabab,其中24,1ac,所以2,3ab.所以曲线C的方程22143xy.(2)因为直线l过椭圆的中心,由椭圆的对称性可知,112ABFAOFSS.因为132ABFS,所以134AOFS.不妨设点11(,)Axy在x轴上方,则1111324AOFSOFy,所以113,32yx,即:A点的坐标为3(3,)2或3(3,)2,所以直线l的斜率为12,故所求直线方程为20xy.4.已知圆C的圆心在抛物线22(0)xpyp上运动,且圆C过(0,)Ap点,若MN为圆C在x轴上截得的弦.(1)求弦长MN;(2)设12,AMlANl,求1221llll的取值范围.解:(1)设00(,)Cxy,则圆C的方程为:22220000()()()xxyyxyp.令0y,并由2002xpy,得2220020xxxxp,解得1020,,xxpxxp从而212MNxxp,(2)设MAN,因为21211sin22MANSllOAMNp,所以2122sinpll,因为l12+l22-2l1l2cosθ=4p2,所以l12+l22=)tan11(4cossin44222ppp.所以22212122211214(1)sintan2(sincos)22sin(45)2pllllllllp.因为0090,所以当且仅当45时,原式有最大值22,当且仅当90时,原式有最小值为2,从而1221llll的取值范围为[2,22].2011届江苏省苏州市迎二模六校联考数学试题5.若双曲线经过点(3,),且渐近线方程是y=±x,则这条双曲线的方程是答案:2219xy10.若点P是曲线y=x2-lnx上的任意一点,则点P到直线y=x-2的最小距离为答案:12.若过点A(a,a)可作圆x2+y2-2ax+a2+2a-3=0的两条切线,则实数a的取值范围是答案:3312aa或18.(本小题满分16分)已知圆C通过不同的三点P(m,0)、Q(2,0)、R(0,1),且圆C在点P处的切线的斜率为1.(1)试求圆C的方程;(2)若点A、B是圆C上不同的两点,且满足•=•,①试求直线AB的斜率;②②若原点O在以AB为直径的圆的内部,试求直线AB在y轴上的截距的范围。18.(1)设圆方程为022FEyDxyx,则圆心)2,2(EDC,且PC的斜率为-1……2分所以120222202401mDEmDFDFE……………………………………………………………5分解得3651mFED,所以圆方程为06522yxyx……………………7分(2)①•=•ABCPABCPCBCACP00)(,所以AB斜率为1…………………10分②设直线AB方程为txy,代入圆C方程得065)62(222ttxtx设),(),,(2211yxByxA,则265337022121ttxxtxxt原点O在以AB为直径的圆的内部,即002121yyxxOBOA………………14分整理得,17170622ttt…………………16分江苏省淮州中学2010—2011学年度第一学期中考试OMNF2F1yx(第18题)高三数学试卷6.若曲线4()fxxx在点P处的切线平行于直线3x-y=0,则点P的坐标为▲.答案:(1,0)二、解答题17.(本小题满分15分)已知点P(1,3),圆C:229()2xmy过点A(1,322),F点为抛物线pxy22(p>0)的焦点,直线PF与圆相切.(1)求m的值与抛物线的方程;(2)设点(2,5)B,点Q为抛物线上的一个动点,求BPBQ的取值范围.解:(Ⅰ)点A代入圆C方程,得22329(1)22m.∴m=1.圆C:229(1)2xy.当直线PF的斜率不存在时不合题意。当直线PF的斜率存在时,设为k,则PF1:(1)3ykx,即30kxyk.∵直线PF与圆C相切,∴2|03|3221kkk.解得1,1kk或.当k=1时,直线PF1与x轴的交点横坐标为2,不合题意,舍去.当k=1时,直线PF1与x轴的交点横坐标为4,42p那么抛物线方程为216yx2(Ⅱ)(1,2)BP,设Q(x,y),(2,5)BQxy,(2)(2)(5)212BPBQxyxy.221216yy21(16)2816y28所以BPBQ的取值范围为,28.江苏连云港市2011届高三上学期第一次调研考试(数学)数学Ⅰ试题10.双曲线22221(0,0)xyabab的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是▲.答案:1,5二、解答题18.(本小题满分16分)如图,椭圆22221xyab(0)ab过点3(1,)2P,其左、右焦点分别为12,FF,离心率12e,,MN是椭圆右准线上的两个动点,且120FMFN.(1)求椭圆的方程;(2)求MN的最小值;(3)以MN为直径的圆C是否过定点?请证明你的结论.解:(1)12cea,且过点3(1,)2P,22222191,42,,abacabc解得2,3,ab椭圆方程为22143xy.…………4分(2)设点12(4,),(4,)MyNy则1122(5,),(3,),FMyFNy1212150FMFNyy,1215yy,又211111151515MNyyyyyy-+≥2,MN的最小值为215.………………………10分(3)圆心C的坐标为12(4,)2yy,半径212yyr.圆C的方程为2221221()(4)()24yyyyxy,整理得:2212128()160xyxyyyyy.…………16分1215yy,22128()10xyxyyy令0y,得2810xx,415x.圆C过定点(415,0).………………16分OFxy··P第22题21.(本小题满分10分)已知动圆P过点1(0,)4F且与直线14y相切.(1)求点P的轨迹C的方程;(2)过点F作一条直线交轨迹C于,AB两点,轨迹C在,AB两点处的切线相交于点N,M为线段AB的中点,求证:MNx轴.解:(1)根据抛物线的定义,可得动圆圆心P的轨迹C的方程为2xy…………4分(2)证明:设221122(,),(,)AxxBxx,∵2yx,∴2yx,∴,ANBN的斜率分别为122,2xx,故AN的方程为21112()yxxxx,BN的方程为22222()yxxxx…7分即21122222yxxxyxxx,两式相减,得122Nxxx,又122Mxxx,∴,MN的横坐标相等,于是MNx………………10分江苏省南通中学2010—2011学年度高三第一学期中考试数学6.若曲线4()fxxx在点P处的切线平行于直线3x-y=0,则点P的坐标为▲.答案:(1,0)2011届江苏高考数学权威预测题7、若双曲线22221(0,0)xyabab的一个焦点到一条渐近线的距离等于焦距的14,则该双曲线的渐近线方程是▲.答案:30xy10、两圆22240()xyaxaaR和224140()xybybbR恰有三条共切线,则11ab的最小值为▲.答案:1、二、解答题18、(16分)如图,在平面直角坐标系中,方程为220xyDxEyF的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.(1)求证:0F;(2)若四边形ABCD的面积为8,对角线AC的长为2,且0ABAD,求224DEF的值;xyHGOAMCBD(3)设四边形ABCD的一条边CD的中点为G,OHAB且垂足为H.试用平面解析几何的研究方法判断点O、G、H是否共线,并说明理由.解:(1)证法一:由题意,原点O必定在圆M内,即点(0,0)代入方程220xyDxEyF的左边后的值小于0,于是有0F,即证.…………4分证法二:由题意,不难发现A、C两点分别在x轴正负半轴上.设两点坐标分别为,0Aa,,0Cc,则有0ac.对于圆方程220xyDxEyF,当0y时,可得20xDxF,其中方程的两根分别为点A和点C的横坐标,于是有ACxxacF.因为0ac,故0F.………………4分(2)不难发现,对角线互相垂直的四边形ABCD面积2ACBDS,因为8S,2AC,可得8BD.………………6分又因为0ABAD,所以A为直角,而因为四边形是圆M的内接四边形,故284BDrr.………………8分对于方程220xyDxEyF所表示的圆,可知22244DEFr,所以2224464DEFr.………………10分(3)证:设四边形四个顶点的坐标分别为,0Aa,0,Bb,,0Cc,0,Dd.则可得点G的坐标为,22cd,即,22cdOG.………………12分又,ABab,且ABOH,故要使G、O、H三点共线,只需证0ABOG即可.而2bdacABOG,且对于圆M的一般方程220xyDxEyF,当0y时可得20xDxF,其中方程的两根分别为点A和点C的横坐标,于是有ACxxacF.………………14分同理,当0x时,可得20yEyF,其中方程的两根分别为点B和点D的纵坐标,于是有BDyybdF.CyxOAB(第12题)yxHAODF1F2所以,02bdacABOG,即ABOG.故O、G、H必定三点共线.………………16分江苏省2011届高三上学期苏北大联考(数学)数学Ⅰ试题3、顶点在原点且以双曲线1322yx的右准线为准线的抛物线方程是★;答案:xy626、在平面直角坐标系xOy中,已知双曲线C:2221xya(0a)的一条渐近线与直线l:210xy垂直,则实数a★;答案:29、曲线C:2sin)(xexxf在0x处的切线方程为★;答案:032yx11、直线250xy与圆222xy相交于,AB两点,O为原点,则OAOB★;答案:012、如图,在平面直角坐标系xOy中,点A为椭圆E:12222byax(0ba)的左顶点,B,C在椭圆E上,若四边形OABC为平行四边形,且∠OAB=30°,则椭圆E的离心率等于★;答案:32213、已知直线01ykx与圆C:422yx相交于A,B两点,若点M在圆C上,且有OBOAOM(O为坐标原点),则实数k=★;答案:0二、解答题16、(本小题共14分)如图,椭圆E:12222byax(0ba)的左、右焦点分别为F1、F2,点A(4,m)在椭圆E上,且0212FFAF,点D(2,0)到直线F1A的距离DH=518.(Ⅰ)求椭圆E的方程;(Ⅱ)设点P位椭圆E上的任意一点,求PDPF1的取值范围。16解:(Ⅰ)由题意知:0,4,0,4,421FFc……………………2分∵,6,518,sin112121DFDHAFAFDFDHFAF又0212FFAF∴abaAFabAF21222,……………………4分∴abaab2226518,则2234ba……………………6分由222acb,得223416bb∴64,4822ab,∴椭圆的方程为:1486422yx。……………………8分(Ⅱ)设点yxP,,则1486422yx,即224348xy∵yxPDyxPF,2,,41∴82221xyxPDPF……………………10分364414024122xxx……………………12分∵88x,∴PDPF1的取值范围为72,36。……………………14分19、(本小题共16分)已知椭圆E:14822yx的左焦点为F,左准线l与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.(Ⅰ)求圆C的方程;(Ⅱ)若直线FG与直线l交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;(Ⅲ)在平面上是否存在一点P,使得21GPGF?若存在,求出点P坐标;若不存在,请说明理由.(1)知:圆C的方程为16)4(22yx……………(4分)江苏省2011年高考数学模拟题5.在平面直角坐标系中,正方形ABCD的中心坐标为(3,2),其一边AB所在直线的方程为x-y+1=0,则边AB的对边CD所在直线的方程为。答案:x-y-3=0。7.若点P(2,0)到双曲线-=1的一条渐近线的距离为,则该双曲线的离心率为。答案:。11.已知在平面直角坐标系xOy中,O(0,0),A(1,-2),B(1,1),C(2.-1),动点M(x,y)满足条件,则\\s\\up8((()·\\s\\up8((()的最大值为。答案:4。四、解析几何题5、已知椭圆x2+=1(0<b<1)的左焦点为F,左、右顶点分别为A,C,上顶点为B,过F、B、C作⊙P,其中圆心P的坐标为(m,n)。(1)当m+n>0时,求椭圆离心率的范围;(2)直线AB与⊙P能否相切?证明你的结论。解:(1)设F、B、C的坐标分别为(-c,0),(0,b),(1,0),则FC、BC的中垂线分别为x=,y-=(x-),联立方程组,解出。m+n=+>0,即b-bc+b2-c>0,即(1+b)(b-c)>0,∴b>c。从而b2>c2,即有a2>2c2,∴e2<,又e>0,∴0<e<。(2)直线AB与⊙P不能相切。由kAB=b,kPB==,如果直线AB与⊙P相切,则b·=-1,又b2+c2=1,解出c=0或2,与0<c<1矛盾,所以直线AB与⊙P不能相切。2011年江苏省海安高级中学、南京外国语学校、南京市金陵中学高三调研测试数学(必试部分)3.抛物线y2=8x的焦点到双曲线–=1的渐近线的距离为______.13.已知椭圆22134xy的上焦点为F,直线10xy和10xy与椭圆相交于点A,B,C,D,则AFBFCFDF.二、解答题18.(本小题满分16分)设圆221:106320Cxyxy,动圆222:22(8)4120Cxyaxaya,(1)求证:圆1C、圆2C相交于两个定点;(2)设点P是椭圆2214xy上的点,过点P作圆1C的一条切线,切点为1T,过点P作圆2C的一条切线,切点为2T,问:是否存在点P,使无穷多个圆2C,满足12PTPT?如果存在,求出所有这样的点P;如果不存在,说明理由.江苏省安宜高级中学10-11年度高三B部数学复习资料期末综合练习(二)4.若抛物线的焦点坐标为(2,0),则抛物线的标准方程是▲.答案:28yx7.已知直线1l:310axy,2l:2(1)10xay,若1l∥2l,则实数a的值是▲.答案:3二、解答题18.(本小题满分16分)已知椭圆E:22184xy的左焦点为F,左准线l与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.(1)求圆C的方程;(2)若直线FG与直线l交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;(3)在平面上是否存在定点P,使得12GFGP?若存在,求出点P坐标;若不存在,请说明理由.18.(1)由椭圆E:22184xy,得l:4x,(4,0)C,(2,0)F,又圆C过原点,所以圆C的方程为22(4)16xy.………………………………4分(2)由题意,得(3,)GGy,代入22(4)16xy,得15Gy,所以FG的斜率为15k,FG的方程为15(2)yx,…………………8分(注意:若点G或FG方程只写一种情况扣1分)所以(4,0)C到FG的距离为152d,直线FG被圆C截得弦长为215216()72.故直线FG被圆C截得弦长为7.…………………………………………………………10分(3)设(,)Pst,00(,)Gxy,则由12GFGP,得22002200(2)12()()xyxsyt,整理得222200003()(162)2160xysxtyst①,…………………………12分又00(,)Gxy在圆C:22(4)16xy上,所以2200080xyx②,②代入①得2200(28)2160sxtyst,…………………………14分又由00(,)Gxy为圆C上任意一点可知,22280,20,160,stst解得4,0st.所以在平面上存在一点P,其坐标为(4,0).…………………………16分江苏常州三中高三数学期末模拟试题11.已知抛物线2:2(0)Cypxp>的准线为l,过(1,0)M且斜率为3的直线与l相交于点A,与C的一个交点为B.若AMMB,则p.214.点P到点A(21,0),B(a,2)及到直线x=-21的距离都相等,如果这样的点恰好只有一个,那么a的值是__________.-21或2118.(本小题满分16分)如图,已知椭圆22221(0)xyabab过点.2(1,)2,离心率为22,左、右焦点分别为1F、2F.点P为直线:2lxy上且不在x轴上的任意一点,直线1PF和2PF与椭圆的交点分别为A、B和C、D,O为坐标原点.(I)求椭圆的标准方程;(II)设直线1PF、2PF的斜线分别为1k、2k.(i)证明:12132kk;(ii)问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率OAk、OBk、OCk、ODk满足0OAOBOCODkkkk?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.江苏省常州市7校2011届高三上学期期中联考(数学理)14、如果关于x的方程213axx在区间(0,)上有且仅有一个解,那么实数a的取值范围为___▲___.20aa或江苏省常州市2011届高三上学期调研试题(数学)6.已知:圆M:0222yyx,直线l的倾斜角为120,与圆M交于P、Q两点,若0OQOP(O为原点),则l在x轴上的截距为.33ABOMPQyxll18.面积为S的ABC的三边cba,,成等差数列,4,60bB,设ABC外接圆的面积为\'S,则SS:\'93414.曲线1:yxC上的点到原点的距离的最小值为.42二、解答题18.(15)已知直线l的方程为2x,且直线l与x轴交于点M,圆22:1Oxy与x轴交于,AB两点(如图).(1)过M点的直线1l交圆于PQ、两点,且圆孤PQ恰为圆周的14,求直线1l的方程;(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;(3)过M点的圆的切线2l交(II)中的一个椭圆于CD、两点,其中CD、两点在x轴上方,求线段CD的长.18、解:(1I)PQ为圆周的1,.42POQO点到直线1l的距离为2.2设1l的方程为22|2|21(2),,.271kykxkk1l的方程为7(2).7yx(2)设椭圆方程为22221(0)xyabab,半焦距为c,则22.ac椭圆与圆O恰有两个不同的公共点,则1a或1.b当1a时,22213,,24cbac所求椭圆方程为22413yx;当1b时,222222,1,2.bcccabc所求椭圆方程为221.2xy(3)设切点为N,则由题意得,椭圆方程为221,2xy在RtMON中,2,1MOON,则30NMO,2l的方程为3(2)3yx,代入椭圆2212xy中,整理得25820.xx设1122(,),(,)CxyDxy,则121282,.55xxxx21212146484(1)[()4]()2.332555CDxxxx江苏省常州市2011届高三复习迎考试卷数学试题Ⅰ12.已知椭圆的中心在坐标原点,焦点在x轴上,以其两个焦点和短轴的两个端点为顶点的四边形是一个面积为4的正方形,设P为该椭圆上的动点,C、D的坐标分别是2,0,2,0,则PC·PD的最大值为▲.414.在平面直角坐标系xOy中,设直线32myx和圆222xyn相切,其中m,*0||1nmnN,,若函数1()xfxmn的零点0(,1),xkkkZ,则k=▲.0二、解答题19.(本小题满分16分)已知椭圆22220yxCabab:+=1>>的离心率为63,过右顶点A的直线l与椭圆C相交于A、B两点,且(13)B,.(1)求椭圆C和直线l的方程;(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线2222440xmxyym与D有公共点,试求实数m的最小值.【解】(1)由离心率63e,得2263aba,即223ab.①………………2分又点(13)B,在椭圆2222:1yxCab+上,即2222(3)(1)1ab+.②………………4分解①②得22124ab,,故所求椭圆方程为221124yx.…………………6分由(20)(13)AB,,,得直线l的方程为2yx.………8分(2)曲线2222440xmxyym,即圆22()(2)8xmy,其圆心坐标为(2)Gm,,半径22r,表示圆心在直线2y上,半径为22的动圆.…………………10分由于要求实数m的最小值,由图可知,只须考虑0m的情形.设G与直线l相切于点T,则由|22|222a,得4m,…………………12分当4m时,过点(42)G,与直线l垂直的直线l的方程为60xy,解方程组6020xyxy,得(24)T,.…………………14分因为区域D内的点的横坐标的最小值与最大值分别为12,,所以切点TD,由图可知当G过点B时,m取得最小值,即22(1)(32)8m,解得min71m.…………………16分(说明:若不说理由,直接由圆过点B时,求得m的最小值,扣4分)江苏省常州市2011届高三复习迎考试卷数学试题Ⅱ(附加题)22.动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4.(1)求点P的轨迹C的方程;(2)过点(0,1)Q作曲线C的切线,求所作的切线与曲线C所围成区域的面积.【解】(1)设P(x,y),根据题意,得22(1)xy+3-y=4,化简,得y=14x2(y≤3).…………………4分(2)设过Q的直线方程为y=kx-1,代入抛物线方程,整理得x2-4kx+4=0.由△=16k2-16=0.解得k=±1.于是所求切线方程为y=±x-1(亦可用导数求得切线方程).切点的坐标为(2,1),(-2,1).由对称性知所求的区域的面积为S=220132(1)d.44xxx…………………10分江苏省常州市北郊中学2011届高三上学期统一练习(数学)4.在平面直角坐标系中,双曲线的中心在原点,焦点在y轴上,一条渐近线方程为30xy,则它的离心率为_______109.已知抛物线)0(22ppxy,过点)0,(p作两条互相垂直的直线21,ll,若1l与抛物线交于QP、两点,若2l与抛物线交于NM、两点,1l的斜率为k,某同学已正确求得弦PQ的中点坐标为),(2kppkp,则弦MN的中点坐标为),(2kpppk二、解答题18.已知⊙O的圆心为原点,与直线0103yx相切,⊙M的方程为4)6()8(22yx,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.(1)求⊙O的方程;(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;(3)求OBOA的最大值与最小值.18.解:(1)⊙O的方程为1022yx(2)由题可知当直线PA过圆M的圆心(8,6)时,弦PQ最大因为直线PA的斜率一定存在,设直线PA的方程为:y-6=k(x-8)又因为PA与圆O相切,所以圆心(0,0)到直线PA的距离为10即101|68|2kk可得91331kk或所以直线PA的方程为:0509130103yxyx或(3)设AOP则2,AOBBOPAOP则1201)(21cos2cos222OPOPOAAOB8210||,12210||minmaxOPOP10200cos||||2OPAOBOBOAOBOA18155)(,855)(minmaxOBOAOBOA19.已知椭圆C的两焦点12,FF均在x轴上,它的一个顶点恰好是抛物线214yx的焦点离心率等于255.点Q在椭圆C外,125FQ,1FQ交椭圆于P点,T是线段2FQ上一点,且0TFPT2,0TF2.(1)求椭圆C的方程;(2)求点T的轨迹E的方程;(3)若M是轨迹E上任意一点,过M点轨迹E的切线与x轴,y轴交于点A,B,ONOAOB,求ON的最小值.19.解(1)抛物线的焦点坐标为(0,1),设椭圆的方程为222210xyabab.由题意知:2222251,,,5,25cbabcaca.∴椭圆的方程为2215xy.(2)111225,25FQFPPQPFPF,∴22,PQPFPQF是等腰三角形.又2220,,PTTFPTTFTQF是的中点.又O是12FF的中点,∴1152OTFQ,∴T的轨迹是圆2250xyy.(3)0000,0Mxyxy.∴O的切线方程为2200005,5xxyyxy.∴22222222200000000551151252525ONxyxyxyxy.又∵2222000000252,,204xyxyxyON∴min25ON.故ON的最小值为25.江苏省成化高中2011届高三(上)期末模拟试卷〈三〉(必做题部分)5.以双曲线2213xy的一条准线为准线,顶点在原点的抛物线方程是2266yxyx或17.(本题满分14分)已知F1(-c,0),F2(c,0)(c>0)是椭圆的两个焦点,O为坐标原点,圆M的方程是22259()416cxcy.(1)若P是圆M上的任意一点,求证:12||||PFPF是定值;(2)若椭圆经过圆上一点Q,且cos∠F1QF2=35,求椭圆的离心率;(3)在(2)的条件下,若|OQ|=342,求椭圆的方程.解:(1)证明:设P(x,y)是圆22259()416cxcy上的任意一点,12||||PFPF=2222222222222295252()162169525()216216ccxcxxcxcxcyccxcxcyxxcxc=3∴12||||PFPF=3----------5分(2)解:在△F1QF2中,F1F2=2c,Q在圆上,设|QF2|=x,则|QF1|=3x,椭圆半长轴长为2x,4c2=x2+9x2-6x2×35,5c2=8x2e2=22()25cx,e=105.--11分(3)由(2)知,x=58c,即|QF2|=58c,则|QF1|=358c22121||||4QOQFQF)cos||||2|||(|4121212221QFFQFQFQFQF2222817)53815285845(41cccc由于|OQ|=342,∴c=2,进一步由e=ca=105得到a2=10,b2=6所求椭圆方程是221106xy.---------16分江阴成化高中11届高三一调模拟试卷四4.双曲线221916xy的渐近线方程为▲.答案:43yx.12.设椭圆22221(0)xyabab>>的两个焦点分别为F1,F2,点P在椭圆上,且120PFPF,12tan2PFF,则该椭圆的离心率等于▲.答案:53.讲评建议:设PF1=m,则PF2=2m,2c=22125PFPFm,2a=3m,22cea.17.如图,已知椭圆C:2221(2)2xyaa的左右焦点分别为F1、F2,点B为椭圆与y轴的正半轴的交点,点P在第一象限内且在椭圆上,且PF2与x轴垂直,15.FPop(Ⅰ)求椭圆C的方程;(Ⅱ)设点B关于直线:yxm的对称点E(异于点B)在椭圆C上,求m的值。解:(1)椭圆C方程为:22142xy,(2)BE⊥l,BE方程:2yx由2221,42yxxy得420,.3xx或422222(,),(,)333323EBEyxmm中点为代入得附加题1、已知点F(0,1),点P在x轴上运动,M点在y轴上,N为动点,且满足0PMPF,PNPM0.(1)求动点N的轨迹C方程;(2)由直线y=-1上一点Q向曲线C引两条切线,切点分别为A,B,求证:AQ⊥BQ.答案:(1)设N(x,y).因PNPM0,故P的坐标为(2x,0),M(0,-y),于是,(,)2xPMy,(,1)2xPF.因0PMPF,即得曲线C的方程为x2=4y.………………5分(2)设Q(m,-1).由题意,两条切线的斜率k均存在,故可设两切线方程为y=k(x-m)-1.将上述方程代入x2=4y,得x2-4kx+4km+4=0.依题意,⊿=(-4k)2-4(4km+4)=0,即k2-mk-1=0.上述方程的两根即为两切线的斜率,由根与系数的关系,其积为-1,即它们所在直线互相垂直.………………10分江阴成化高中2011届高三第一次调研模拟试卷一6.若实数m、n{1,1,2,3},且nm,则曲线122nymx表示焦点在y轴上的双曲线的概率是.4113.设P是椭圆1162522yx上任意一点,A和F分别是椭圆的左顶点和右焦点,则AFPAPFPA41的最小值为918.已知⊙),1,2(1:22AyxO和定点由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足.||||PAPQ(1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。18.解:(1)连OP,Q为切点,PQ⊥OQ,由勾股定理有222||||||OQOPPQ又由已知22|||||,|||PAPQPAPQ故即:22222)1()2(1)(baba化简得实数a、b间满足的等量关系为:032ba…………………4分(2)由032ba,得b=-2a+3。1||22baPQ81251)32(222aaaa.54)56(52a故当552||,56minPQa时,即线段PQ长的最小值为552………………8分(3)设⊙P的半径为R,OP设⊙O有公共点,⊙O的半径为1,.1|||1||,1|||1|OPROPRROPR且即而2222)32(||aabaOP.59)56(52a故当.1553,5332,553||,56minminRabPQa此时时得半径取最小值⊙P的方程为222)1553()53()56(yx……………14分江苏省成化高中2011届高三(上)期末模拟试卷〈二〉7.已知圆22(2)9xy和直线ykx交于A,B两点,O是坐标原点,若2OAOBO,则||AB .310214.我们可以运用下面的原理解决一些相关图形的面积问题:如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k,那么甲的面积是乙的面积的k倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是22221(0)xyabab与222xya,运用上面的原理,图③中椭圆的面积为.ab17.设椭圆2222:1(0)xyCabab的上顶点为A,椭圆C上两点,PQ在x轴上的射影分别为左焦点1F和右焦点2F,直线PQ的斜率为32,过点A且与1AF垂直的直线与x轴交于点B,1AFB的外接圆为圆M.Oxyxl①②③甲甲乙乙(将l向右平移)(1)求椭圆的离心率;(2)直线213404xya与圆M相交于,EF两点,且212MEMFa,求椭圆方程;(3)设点(0,3)N在椭圆C内部,若椭圆C上的点到点N的最远距离不大于62,求椭圆C的短轴长的取值范围.17.解:(1)由条件可知abcP2,,abcQ2,因为23PQk,所以得:e12………4分(2)由(1)可知,cbca3,2,所以,0,3,0,,3,01cBcFcA,从而0,cM半径为a,因为212MEMFa,所以120EMF,可得:M到直线距离为2a从而,求出2c,所以椭圆方程为:2211612xy;………9分(3)因为点N在椭圆内部,所以b>3………10分设椭圆上任意一点为yxK,,则2222263yxKN由条件可以整理得:018941822byy对任意3,bbby恒成立,所以有:0189418922bbbb或者018949189922bb解之得:2b(6,1226]………15分东海高级中学2011届高三理科数学30分钟限时训练(06)4、双曲线22194xy的一个焦点到一条渐近线的距离是 2东海高级中学2011届高三理科数学30分钟限时训练(09)8.一椭圆的四个顶点为A1,A2,B1,B2,以椭圆的中心为圆心的圆过椭圆的焦点且与菱形1122ABAB相切,则椭圆的离心率为215东海高级中学2011届高三理科数学30分钟限时训练(10)5.已知椭圆C以坐标原点为中心,坐标轴为对称轴,且椭圆C以抛物线216xy的焦点为焦点,以双曲线221169yx的焦点为顶点,则椭圆C的标准方程为221259yx7.若直线022byax),(Rba始终平分圆014222yxyx的周长,则ab的最大值是14东海高级中学2011届高三理科数学30分钟限时训练(01)5.已知直线1l:32xy,直线2l与直线1l关于直线xy对称,则直线2l的斜率为_______.0.58.已知直线0132yx与圆032-22xyx交于NM,两点,则弦MN的垂直平分线方程为__________.3x-2y-3=0东海高级中学2011届高三理科数学30分钟限时训练(02)2、若双曲线12222byax的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是___________.56、过点0,4作直线l与圆0204222yxyx交于A、B两点,若AB=8,则直线l的方程为_____________.020125yx或4x东海高级中学2011届高三理科数学30分钟限时训练(03)7、过定点P(1,2)的直线在xy轴与轴正半轴上的截距分别为ab、,则422ab的最小值为.32东海高级中学2011届高三理科数学30分钟限时训练(04)3、抛物线yx82的准线方程为.2y4、双曲线012222babyax的离心率为26,则椭圆12222byax的离心率为.22东海高级中学2011届高三理科数学30分钟限时训练(05)7、已知A(0,b),B为椭圆22xa+22yb=1(a>b>0)的左准线与x轴的交点,若线段AB的中点C在椭圆上,则该椭圆的离心率为______33江苏省东海高级中学2011届高三上学期期中考试试题(数学)7、已知直线0xya与圆221xy交于A、B两点,且向量OA、OB满足OAOBOAOB,其中O为坐标原点,则实数a的值为▲.18、在平面直角坐标系xOy中,O是坐标原点,设函数()(2)3fxkx的图象为直线l,且l与x轴、y轴分别交于A、B两点,给出下列四个命题:①存在正实数m,使△AOB的面积为m的直线l仅有一条;②存在正实数m,使△AOB的面积为m的直线l仅有两条;③存在正实数m,使△AOB的面积为m的直线l仅有三条;④存在正实数m,使△AOB的面积为m的直线l仅有四条.其中所有真命题的序号是▲.②③④17、(14分)已知圆2522yx,ABC内接于此圆,A点的坐标)4,3(,O为坐标原点.⑴若ABC的重心是)2,35(G,求直线BC的方程;⑵若直线AB与直线AC的倾斜角互补,求证:直线BC的斜率为定值.17.解:(1)设1122(,),(,)BxyCxy由题意可得:12123533423xxyy即12121212xxyy....3分又221122222525xyxy相减得:12121212()()()()0xxxxyyyy.............5分∴12121yyxx∴直线BC的方程为1(1)yx,即20xy............7分(2)设AB:(3)4ykx,代入圆的方程整理得:2222(1)(86)92490kxkkxkk.............9分∵13,x是上述方程的两根∴221122383464,11kkkkxykk........11分同理可得:222222383464,11kkkkxykk∴121234BCyykxx...........14分江苏省东海高级中学2011届高三上学期周周练十(数学)4.若,,lmn是三条互不相同的空间直线,,是两个不重合的平面,则下列命题中为真命题的是▲.④①若//,,,ln则//ln;②若,,l则l;③若,,lnmn则//lm;④若,//,ll则.7.已知点A是直角三角形ABC的直角顶点,且(,2),(4,),(1,1)AaBaCa,则三角形ABC的外接圆的方程是▲.5)2(22yx9.已知P是以21,FF为焦点的椭圆)0(12222babyax上的一点,若021PFPF,21tan21FPF,则此椭圆的离心率为▲.3518.(本题满分16分)在平面直角坐标系xOy中,已知以O为圆心的圆与直线l:(34)ymxm,()mR恒有公共点,且要求使圆O的面积最小.(1)写出圆O的方程;(2)圆O与x轴相交于A、B两点,圆内动点P使||PA、||PO、||PB成等比数列,求PAPB的范围;(3)已知定点Q(4,3),直线l与圆O交于M、N两点,试判断tanQMQNMQN是否有最大值,若存在求出最大值,并求出此时直线l的方程,若不存在,给出理由.18.解:(1)因为直线l:(34)ymxm过定点T(4,3),由题意,要使圆O的面积最小,定点T(4,3)在圆上,所以圆O的方程为2225xy.……………………4分(2)A(-5,0),B(5,0),设00(,)Pxy,则220025xy……①00(5,)PAxy,00(5,)PBxy,由||,||,||PAPOPB成等比数列得,2||||||POPAPB,即222222000000(5)(5)xyxyxy,整理得:2200252xy,即2200252xy…②由(1)(2)得:202504y,22200025(25)22PAPBxyy,25[,0)2PAPB………………10分(3)tan||||costanQMQNMQNQMQNMQNMQN||||sin2MQNQMQNMQNS.……………………12分由题意,得直线l与圆O的一个交点为M(4,3),又知定点Q(4,3),直线MQl:3y,||8MQ,则当(0,5)N时MQNS有最大值32.………14分即tanQMQNMQN有最大值为64,此时直线l的方程为250xy.………16分江苏省东海高级中学2011届高三上学期自主探究试题11(数学)17.(14分)如图,反比例函数()yfx(0x)的图像过点(1,4)A和(4,1)B,点(,)Pxy为该函数图像上一动点,过P分别作x轴、y轴的垂线,垂足为C、D.记四边形OCPD(O为坐标原点)与三角形OAB的公共部分面积为S.(1)求S关于x的表达式;(2)求S的最大值及此时x的值.17.解:(1)由题设,得4()fxx(0x),……………………2分BAyxOCPD当1x≤时,2158Sx,当14x时,22248xSx,当4x≥时,230Sx,故222215,1,824,14,830,4.xxxSxxxx≤≥……………………7分)(2)易知当1x≤时,2158Sx为单调递增函数,158S≤,…………9分当4x≥时,230Sx为单调递减函数,158S≤,…………11分当14x时,22248xSx在区间(1,2)上单调递增,在区间(2,4)上单调递减,(证明略),得1538S≤,故S的最大值为3,此时2x.…………14分江苏省东海县高级中学2011届高三理科数学练习十三5.已知l是直线,,是两个不同的平面,则下列命题中:①若//l,//l,则//.②若,//l,则l.③若l,//l,则.④若//,//l,则//l.其中是真命题的序号是.③6.若PQ是圆229xy的弦,若PQ的中点是(1,2)M,则弦PQ的长度为.410.设P为曲线2:1Cyxx上一点,曲线C在点P处的切线的斜率的范围是[1,3],则点P纵坐标的取值范围是.3[,3]412.已知椭圆22221(0)xyabab的左、右焦点分别为12(,0),(,0)FcFc,若椭圆上存在一点P,使1221sinsinacPFFPFF,则椭圆离心率的取值范围为.(21,1)18.设12,FF分别是椭圆2222:1(0)xyCabab的左、右焦点,(1)设椭圆C上的点3(3,)2到两点12,FF距离之和等于4,写出椭圆的方程;(2)设K是(Ⅰ)中椭圆C上的动点,求以线段1KF为直径的圆的圆心轨迹方程;(3)设点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于,MN两点,当直线,PMPN的斜率都存在,并记为,PMPNkk,试探究PMPNkk的值是否与点P及直线L有关,并证明你的结论.18.答案:①221,(1,0)43xy,②2214()123xy,③22PMPNbkka江苏省东海县高级中学2011届高三上学期练习十四(数学理)7.将圆xyx沿122轴正方向平移1个单位后得到圆C,若过点(3,0)的直线l和圆C相切,则直线l的斜率为3310.若椭圆的中心为原点O,右焦点为F,右准线为l,若在l上存在点M,使线段OM的垂直平分线经过F,则椭圆离心率的取值范围为.1,2218.已知动⊙M经过点(2,0)D,且与圆22:40Cxyx外切(1)求点M的轨迹方程;(2)记半径最小的圆为⊙0M,直线l与⊙0M相交于,AB两点,且⊙0M上存在点P,使得000(1,3)MPMAMB(0).①求⊙0M的方程;②求直线l的方程及相应的点P坐标.18.解:(1)圆C半径R=2,C(3,0)--------1分由题意可得,MC=MD+2,MC—MD=2
展开内容










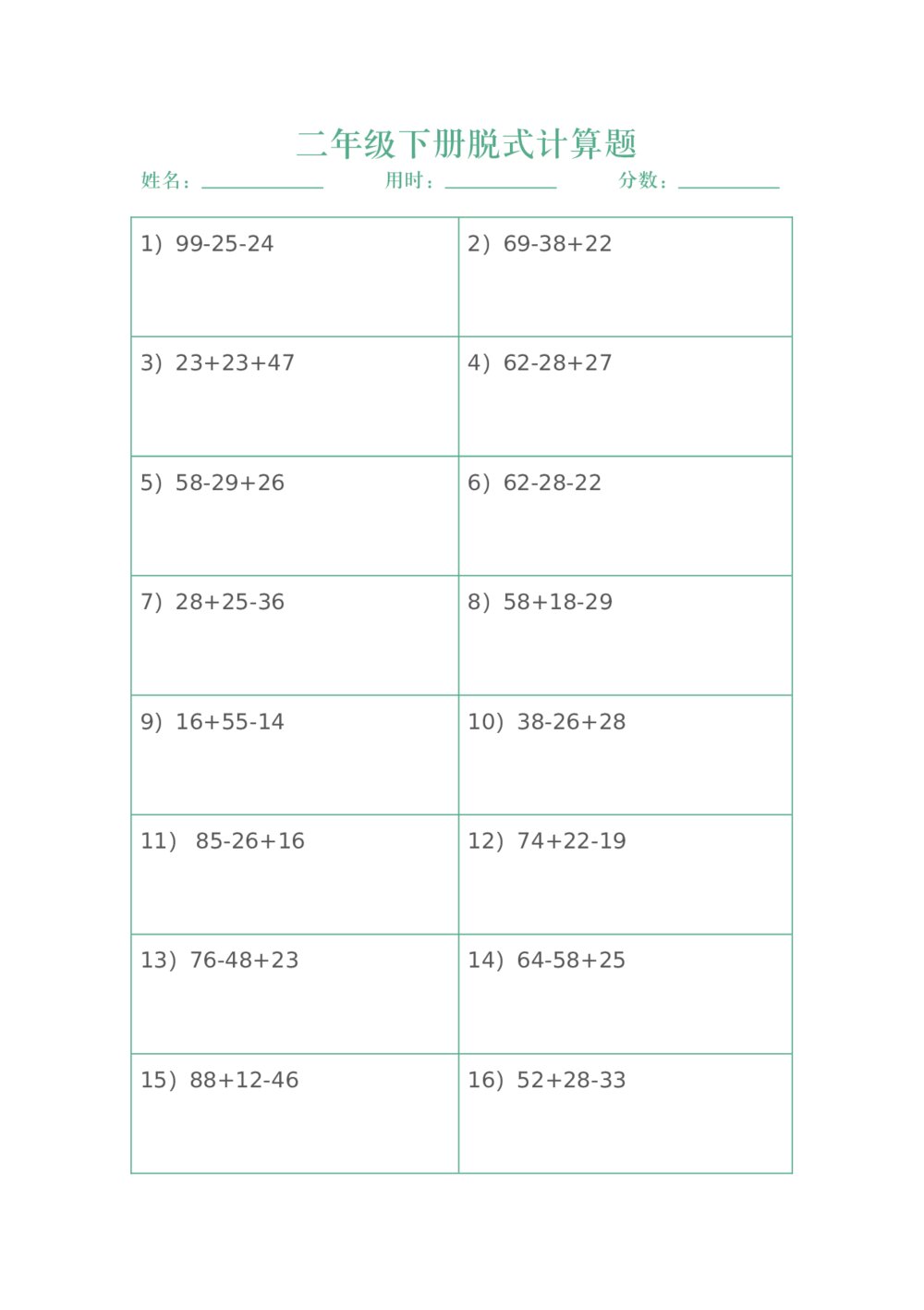 二年级数学下册脱式计算题练习word版+参考答案
二年级数学下册脱式计算题练习word版+参考答案 2017年高考数学知识方法专题8《第40练 随机变量及其分布列》
2017年高考数学知识方法专题8《第40练 随机变量及其分布列》 2014年全国统一高考数学试卷(理科)(新课标ⅰ)+参考答案解析
2014年全国统一高考数学试卷(理科)(新课标ⅰ)+参考答案解析 2015年丰台区高三年级第二学期统一练习数学(理科)试题+答案解析PDF版
2015年丰台区高三年级第二学期统一练习数学(理科)试题+答案解析PDF版 最新6年高考4年模拟试题试卷--第九章第一节直线和圆(答案解析)
最新6年高考4年模拟试题试卷--第九章第一节直线和圆(答案解析) 2018年山东高考(文科)数学真题试卷+参考答案
2018年山东高考(文科)数学真题试卷+参考答案