









试读已结束,还剩93页未读,您可下载完整版后进行离线阅读
《2012年江苏省高考数学一轮训练试题考点2《函数导数》》是由用户上传到老师板报网,本为文库资料,大小为4.71 MB,总共有103页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 103页
- 4.71 MB
- VIP模板
- doc
- 数字产品不支持退货
(新沂市第一中学2011届高三数学)6.二次函数2()fxaxbxc(a、b、cR),若a、b、c成等比数列且(0)1f,则函数()fx的最大值为▲.54(新沂市第一中学2011届高三数学)10.若函数f(x)对于任意的x都有f(x+2)=f(x+1)-f(x)且f(1)=lg3-lg2,f(2)=lg3+lg5,则f(2010)=▲.-1(新沂市第一中学2011届高三数学)20.(本小题满分16分)已知函数2()fxx,()2ln(0)gxexx(e为自然对数的底数),它们的导数分别为()fx、()gx.(1)当0x时,求证:()()4fxgxe;(2)求()()()(0)Fxfxgxx的单调区间及最小值;(3)试探究是否存在一次函数(,)ykxbkbR,使得()fxkxb且()gxkxb对一切0x恒成立,若存在,求出该一次函数的表达式;若不存在,请说明理由.20.解:(1)∵0x,2()2,()efxxgxx,∴()()2()224efxgxxeex,当且仅当exx,即xe时,等号成立.∴()()4fxgxe.…………………4分(2)22()()()()2()exeFxfxgxxxx(0x),令()0Fx,得xe(xe舍),∴当0xe时,()0Fx,()Fx在(0,)e上单调递减;当xe时,()0Fx,()Fx在(,)e上单调递增.…………………………8分∴当xe时,()Fx有极小值,也是最小值,即min()()2ln0FxFeeee.∴()Fx的单调递增区间为(,)e,单调递减区间为(0,)e,最小值为0.…………………10分(3)由(2)知,()fx与()gx的图象有且仅有一个公共点(,)ee,∴猜想:一次函数的图像就是()fx与()gx的图象在点(,)ee处的公切线,其方程为2yexe.………………………………………………………12分下面证明:当0x时,()2fxexe,且()2gxexe恒成立.又∵2()(2)()fxexexe0,∴()2fxexe对0x恒成立.又令()2()22lnGxexegxexeex,∴22()()2eexeGxexx,∴当0xe时,()0Gx,()Gx在(0,)e上单调递减;当xe时,()0Gx,()Gx在(,)e上单调递增.∴当xe时,()Gx有极小值,也是最小值,即min()()22ln0GxGeeeee,∴()0Gx,即()2gxexe恒成立.故存在一次函数2yexe,使得当0x时,()2fxexe,且()2gxexe恒成立.……………………………………………………………………………………16分(新沂市第一中学2011届高三上学期阶段性自主测试)13.已知函数()||,()fxxxpxqxR,给出下列四个命题:①()fx为奇函数的充要条件是0q;②)(xf的图象关于点(0,)q对称;③当0p时,方程()0fx的解集一定非空;④方程()0fx的解的个数一定不超过两个。其中所有正确命题的序号是_____▲____(1)(2)(3)___(新沂市第一中学2011届高三上学期阶段性自主测试)19..(本小题16分)已知函数f(x)=alnx+2x(a为实常数).(1)若a=-2,求证:函数f(x)在(1,+.∞)上是增函数;(2)求函数f(x)在[1,e]上的最小值及相应的x值;(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.19.(1)当2a时,xxxfln2)(2,当),1(x,0)1(2)(2xxxf,故函数)(xf在),1(上是增函数.…………………………4分(2))0(2)(2xxaxxf,当],1[ex,]2,2[222eaaax.若2a,)(xf在],1[e上非负(仅当2a,x=1时,0)(xf),故函数)(xf在],1[e上是增函数,此时min)]([xf1)1(f. ……………6分若222ae,当2ax时,0)(xf;当21ax时,0)(xf,此时)(xf是减函数;当exa2时,0)(xf,此时)(xf是增函数.故min)]([xf)2(af2)2ln(2aaa.若22ea,)(xf在],1[e上非正(仅当2e2a,x=e时,0)(xf),故函数)(xf在],1[e上是减函数,此时)()]([minefxf2ea.………………8分综上可知,当2a时,)(xf的最小值为1,相应的x值为1;当222ae时,)(xf的最小值为2)2ln(2aaa,相应的x值为2a;当22ea时,)(xf的最小值为2ea,相应的x值为e.…………………………………………10分(3)不等式xaxf)2()(,可化为xxxxa2)ln(2.∵],1[ex,∴xx1ln且等号不能同时取,所以xxln,即0lnxx,因而xxxxaln22(],1[ex)……………………………………………12分令xxxxxgln2)(2(],1[ex),又2)ln()ln22)(1()(xxxxxxg,………14分当],1[ex时,1ln,01xx,0ln22xx,从而0)(xg(仅当x=1时取等号),所以)(xg在],1[e上为增函数,故)(xg的最小值为1)1(g,所以a的取值范围是),1[.……………16分(新沂市第一中学2011届高三上学期阶段性自主测试)20、已知定理:“若,ab为常数,()gx满足()()2gaxgaxb,则函数()ygx的图象关于点(,)ab中心对称”.设函数1()xafxax,定义域为A.(1)试证明()yfx的图象关于点(,1)a成中心对称;(2)当[2,1]xaa时,求证:1()[,0]2fx;(3)对于给定的1xA,设计构造过程:21(),xfx32()xfx,…,1()nnxfx.如果(2,3,4...)ixAi,构造过程将继续下去;如果ixA,构造过程将停止.若对任意1xA,构造过程可以无限进行下去,求a的值.20、解(1)∵1()1fxax,∴11()()(1)(1)2faxfaxxx.由已知定理,得()yfx的图象关于点(,1)a成中心对称.(2)先证明()fx在[2,1]aa上是增函数,只要证明()fx在(,)a上是增函数.设12xxa,则1212121211()()0()()xxfxfxaxaxaxax,∴()fx在(,)a上是增函数.再由()fx在[2,1]aa上是增函数,得当[2,1]xaa时,()[(2),(1)]fxfafa,即1()[,0]2fx.(3)∵构造过程可以无限进行下去,∴1()xafxaax对任意xA恒成立.∴方程1xaaax无解,即方程2(1)1axaa无解或有唯一解xa.∴210,10,aaa或210,1.1aaaaa由此得到1a.8、已知函数fx()在R上可导,且222fxxxf()(),则1f()与1f()的大小关系为A.1f()=1f()B.11ff()C.11ff()D.不确定9、若函数f(x)=kax-a-x(a>0且a≠1)在(-∞,+∞)上既是奇函数,又是增函数,则g(x)=loga(x+k)的图象是16、设函数).(cossin32cos2)(2Rxmxxxxf(I)求函数)(xf的最小正周期;(II)若].27,21[)(],2,0[的值域恰为的值使函数求xfmx17、设)(xf是定义在,0上的单调递增函数,满足1)3(),()()(fyfxfxyf,求:(Ⅰ)1f;(Ⅱ)若28xfxf,求x的取值范围13、函数)0()01)(sin()(12xexxxfx。若2)()1(aff,则a的值为2010-2011学年度第一学期江苏省南通市六所省重点高中联考试卷数学Ⅰ试题2011.114、设函数2()(0)fxaxbxca的定义域为D,若所有点(,())(,)sftstD构成一个正方形区域,则a的值为▲20、(本题满分16分)设0a,函数2()|ln1|fxxax.(Ⅰ)当2a时,求函数()fx的单调增区间;(Ⅱ)若[1,)x时,不等式axf)(恒成立,实数a的取值范围.解:(1)当2a时,2()2ln1fxxx222ln2(0)2ln2()xxxexxxe…………(2分)当0xe时,2222()2xfxxxx,()fx在(1,]e内单调递增;2当xe时,2()20fxxx恒成立,故()fx在[,)e内单调递增;()fx的单调增区间为(1,)。…………(6分)(2)①当xe时,2()lnfxxaxa,()2afxxx()xe0a,()0fx恒成立,()fx在,e上增函数。故当xe时,2min()yfee。…………(8分)②当1xe时,2()lnfxxaxa,2()2()()22aaafxxxxxx(1)xe(Ⅰ)当12a,即02a时,()fx在(1,)xe时为正数,所以()fx在区间[1,)e上为增函数。故当1x时,min1ya,且此时(1)()ffe…………(10分)(Ⅱ)当12ae,即222ae时,()fx在(1,)2ax时为负数,在(,)2axe时为正数,所以()fx在区间[1,)2a上为减函数,在(,)2ae上为增函数。故当2ax时,min3ln222aaay,且此时()()2affe。…………(12分)(Ⅲ)当2ae,即22ae时,()fx在(1,)xe进为负数,所以()fx在区间[1,]e上为减函数,故当xe时,2min()yfee。…………(14分)所以函数()yfx的最小值为2min221,023ln,22222,2aaaaayaeeae。由条件得102aaa此时02a;或23ln22222aaaaae,此时22ae;或222eaae,此时无解。综上,02ae。…………(16分)江苏省2010高考数学模拟题(压题卷)1.已知函数31xxy的最大值为M,最小值为m,则mM的值为2.2.已知函数)(log2xaxya在区间[2,4]上是增函数,则实数a的取值范围是),1(.四、导数题1.汶川大地震后,为了消除某堰塞湖可能造成的危险,救授指挥部商定,给该堰塞湖挖一个横截面为等腰梯形的简易引水槽(如图所示)进行引流,已知等腰梯形的下底与腰的长度都为a,且水槽的单位时间内的最大流量与横载面的面积为正比,比例系数0k.(1)试将水槽的最大流量表示成关于的函数()f;(2)为确保人民的生命财产安全,请你设计一个方案,使单位时间内水槽的流量最大(即当为多大时,单位时间内水槽的流量最大).解:(1)设水槽的横截面面积为s,则21[(2cos)]sinsin(1cos).2saaaaa所以2()sin(1cos),(0,).2fksak(2)因为22()(2coscos1)fak,令()0f,则22coscos10.解得1cos2或cos1,由02知cos1,所以1cos,.23当03时,()0f,即()f在(0,)3上递增,当32时,()0f,即()f在(,)32上递减,所以当3时,水槽的流量最大,即设计成3的等腰梯形引水槽,可使单位时间内水槽的流量最大.2.某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.(1)过点p的一条直线与走廊的外侧两边交于,AB两点,且与走廊的一边的夹角为(0)2,将线段AB的长度l表示为的函数;(2)一根长度为5m的铁棒能否水平(铁棒与地面平行)通过该直角走廊?请说明理由(铁棒的粗细忽略不计).解:(1)根据图得22(),(0,).sincos2lBPAP(2)解法1:铁棒能水平通过该直角直廊,理由如下:22()()()sincosl220sin2cos0cos2sinsincos22222(sincos).sincos令()0l得,4.当04时,()0,()ll为减函数;当42时,()0,()ll为增函数;所以当4时,()l有最小值42,因为425,所以铁棒能水平通过该直角走廊.解法2:铁棒能水平通过该直角走廊,理由如下:22222(sincos)4(12sincos)[()][]sincossincosl224814(1)4(sincos)sincossincos224(1)4sin2,因为(0,)2,所以2(0,),所以当2,24时,2sin2有最小值2.所以2[()]l有最小值32,()l有最小值42,因为425,所以铁棒能水平通过该直角走廊.3.已知函数2()4(2)lnfxxxax,(Ra,且0a).(1)当18a时,求函数()fx的单调区间;(2)求函数()fx在区间2[e,e]上的最小值.解:(1)当18a时2()416ln(0)fxxxxx,162(2)(4)()24.xxfxxxx由()0fx,解得4x或20.x注意到0x,所以函数()fx的单调递增区间是(4,).由()0fx,解得04x或2x,注意到0x,所以函数()fx的单调递减区间是(0,4).综上所述,函数()fx的单调递增区间是(4,),单调递减区间是(0,4).(2)当2[e,e]x时,2()4(2)ln,fxxxax22242()24axxafxxxx,设2()242gxxxa,当0a时,有1642(2)80aa,此时()0gx恒成立,所以()0,()fxfx在2[e,e]上单调递增,所以2min()(e)e4e2.fxfa当0a时,1642(2)80aa,令()0fx,即22420xxa,解得212ax或212ax;令()0fx,即22420xxa,解得2211.22aax①当221e,2a即222(e1)a时()fx在区间2[e,e]上单调递减,所以242min()(e)e4e42fxfa;②当22e1e2a,即2222(e1)2(e1)a时,()fx在区间2[e,1]2a上单调递减,在区间22[1,e]2a上单调递增,所以min22()(1)23(2)ln(1)222aaafxfaa;③当21e2a,即202(e1)a时,()fx在区间2[e,e]上单调递增,所以2min()(e)e4e2.fxfa综上所述,当222(e1)a时,42min()e4e42fxa;当2222(e1)2(e1)a时,min2()23(2)ln(1)22aafxaa;当0a或202(e1)a时,2min()e4e2.fxa4.函数3()3fxxx.(1)求函数()fx的极值;(2)已知()fx在[,2]tt上是增函数,求t的取值范围;(3)()fx在[,2]tt上最大值M与最小值m之差Mm为()gt,求()gt的最小值.解:(1)2()33fxx,令()0fx,1x,x(,1)1(1,1)1(1,)()fx+0-0+()fx2-2所以,()fx极大=(1)2f,()fx极小=(1)2.f(2)()fx在[,2]tt上是增函数,必须有21t或1t,所以t的取值范围是(-∞,-3]∪[1,∞).(3)当3t时,()mft,(2)Mft,2()6122gtMmtt,令(2)()ftft,261220tt,613t,当6313t时,()mft,2M,3()32gttt,当6113t时,(2)mft,2M,32()69gtttt,当6113t,2m,()Mft,3()32gttt,当6113t时,2m,(2)Mft,32()694gtttt,当1t时,()mft,(2)Mft,2()6122gttt.233233226122(3),632(31),3669(11),3()632(11),36694(11),36122(1),ttttttttttgttttttttttt()gt最小值为6626(1)(1)2339gg.六、函数题3.已知函数2()(xxfxaxaR,1)a,(1)求函数f(x)的值域;(2)记函数()(),2,gxfxx,若()gx的最小值与a无关,求a的取值范围;(3)若22m,直接写出(不需给出演算步骤)关于x的方程()fxm的解集.解:(1)①0x时,221,()22xxxxxafxaaaa,当且仅当2xxaa,即21xa时等号成立;②0x,31,01,()3xxaafxa,由①②知函数()fx的值域为[22,).(2)()()2,[2,)xxgxfxaax,①0x,1,1,()3,()3xxaagxagx,②20x时,211,1,()2xxxaagxaaa,令xta,则1()2gxtt,记1()2.httt21(1)ta,1()222httt,当且仅当12tt,22t时等号成立,(i)2122a,即42a时,结合①知min()22gx与a无关;(ii)2122a,即412a时,421()220htat,()ht在21[,1)a上是增函数,2minmin2212()()()3gxhthaaa,结合①知2min22()gxaa与a有关;综上,若()gx的最小值与a无关,则实数a的取值范围是42a.(3)①223m时,关于x的方程()fxm的解集为28|log2ammxx;②m>3时,关于x的方程()fxm的解集为28|log2ammxx或3logaxm.4.已知函数12()3,()(,fxaxgxbxcxabR)且1()(1)(0)2ggf.(1)试求,bc所满足的关系式;(2)若0b,方程()()fxgx在(0,)有唯一解,求a的取值范围;(3)若1b,集合|()(),()0Axfxgxgx,试求集合A;解:(1)由1()(1)(0)2ggf,得(24)()3bcbc,,bc所满足的关系式为10bc.(2)由0,10bbc,可得1c,方程()()fxgx,即23axx,可化为133axx,令1xt,则由题意可得,33att在(0,)上有唯一解.令3()3(0)htttt,由2()330htt,可得1t,当01t时,由()0ht,可知()ht是增函数;当1t时,由()0ht,可知()ht是减函数,故当1t时,()ht取极大值2;由函数()ht的图象可在,当2a或0a时,方程()()fxgx有且仅有一个正实数解.故所求a的取值范围为2aa或0a.(3)由1,10bbc,可得0c,|()()Axfxgx且1()0|3gxxaxx且20|310xxaxx且0x,当0a时,394(,0)2aAa;当0a时,1(,0)3A;当94a时,(940),(,0)aA;当94a时,|0Axx且23x;当904a时,394394(,)(,0)22aaAaa.5.已知()1(0,0)fxAxBxAB.(1)求()fx的定义域;(2)求()fx的最大值和最小值;(3)若()11(0)gxmxnxmn,如何由(2)的结论求g(x)的最大值和最小值.解:(1)()fx的定义域为[0,1].(2)222222()(1)ABfxABxxABAB,设22cos,cos,(0,),2AxAB22sin,1sinBxAB,则22()cos(),fxAB当时,222[0,1]AxAB,此时()fx最大值为22AB,又cos()在222[0,]AAB递增,在222[,1]AAB递减,()fx的最小值是(0)f与(1)f的较小者,即A与B的较小者.(3)设111()xtnmm,11[,],[0,1],xtmn则1111()()()()(1)gxktmtntnmnm,由(2)知g(x)的最大值为1111()()mnmnnmnmnm,最小值为11()mnm和11()nnm的较小者,即1nm.6.已知2()log,fxx当点(,)Mxy在()yfx的图象上运动时,点(,)Nxny在函数()nygx的图象上运动()nN.(1)求()nygx的解析式;(2)求集合Aa关于x的方程12(2)()gxgxa有实根,Ra;(3)设()1()()2ngxnHx,函数11()()(),(0)FxHxgxaxb的值域为1,3,2求证:1,22ab.解:(1)由条件知()()nyfxnygx,又22()log()lognfxxgxnx.(2)方程12(2)()gxgxa即2xxa,求集合A就是求方程2xxa有实根时a的范围.而21992(2)244axxx,94a时原方程总有实根,9,4A,(3)2log2111()()()log,(0)2nxnnHxFxxaxbxx,又\'211()0,()ln2FxFxxx在,ab上递减,()31()2FaFb,即2213log11log2aabb①,由1ytx与2logyx的图象只有唯一交点知:方程21logtxx只有唯一解,经检验122ab是方程组①的唯一解,故得证.七、理科附加题3.设函数21321()e(R).3xfxxxxx(1)求函数()yfx的单调区间;(2)求()yfx在[1,2]上的最小值;(3)当(1,)x时,用数学归纳法证明:nN*,1e.!nxxn解:(1)12121()2ee2(2)(e1)xxxfxxxxxxx,令()0fx,可得12x,20x,31.x当x变化时,()fx,()fx的变化情况如下表:x(,2)2(2,0)0(0,1)1(1,)()fx-0+0-0+()fx极小值极大值极小值函数()yfx的增区间为(2,0)和(1,),减区间为(,2)和(0,1).(2)当[1,2]x时,212(1)0,e3f5(2)4(e)0,()3ffx极小值1(1)(1),()3fffx极大值(0)0f.所以()fx在[1,2]上的最小值为212.e3(3)设1()e!nxnxgxn,当1n时,只需证明11()e0xgxx,当(1,)x时,11()e10xgx,所以11()exgxx在(1,)上是增函数,011()(1)e10gxg,即1exx;当(1,)x时,假设nk时不等式成立,即1()e0!kxkxgxk,当1nk时,因为111(1)()ee0(1)!!kkxxkkxxgxkk,所以1()kgx在(1,)上也是增函数.所以01111()(1)e10(1)!(1)!kkgxgkk,即当1nk时,不等式成立.由归纳原理,知当(1,)x时,nN*,1e.!nxxn2011届江苏省苏州市迎二模六校联考数学试题14.已知函数f(x)=ax2-2•x,g(x)=-,若存在x0,使得f(x0)是f(x)的最大值,g(x0)是g(x)的最小值,则这样的整数对(a,b)为答案:(-1,-1)(-1,3)20.(本题满分16分)已知函数f(x)=x(x-a)(x-b),点A(m,f(m)),B(n,f(n)).(1)设b=a,求函数f(x)的单调区间;(2)若函数f(x)的导函数f’(x)满足:当|x|≤l时,有|f’(x)|≤恒成立,求函数f(x)的表达式;(3)若00,由(1)知,在x=a处有极小值也是最小值f(a),f(a)=0,即ln10aa.令()ln1gaaa,/11()1agaaa.当01a时,/()0ga,在(0,1)上单调递增;当a>1时,/()0ga,在(1,)上单调递减.max()(1)0gag,()ga=0只有唯一解a=1.()fx=0在(0,)上有唯一解时必有a=1.……………………………………12分综上:在a>0时,=0在(0,)上有唯一解的充要条件是a=1.(3)证明:∵10时,由对数函数性质,f(x)的值域为R;当m=0时,2()02xfx对0x,()0fx恒成立;……………………6分当m<0时,由()0mfxxxmx,列表:min()()ln.2mfxfmmm这时,minln0()0e<0.20mmmfxmm,……………………8分x(0)m,m()m,()fx-0+()fx减极小增所以若0x,()0fx恒成立,则实数m的取值范围是(e0],.故0x使()0fx成立,实数m的取值范围(,e]0,.………………10分(3)因为对[1]xm,,(1)()()0xxmHxx,所以()Hx在[1,]m内单调递减.于是21211|()()|(1)()ln.22HxHxHHmmmm2121113|()()|1ln1ln0.2222HxHxmmmmmm…………………12分记13()ln(1e)22hmmmmm,则221133111()022332h\'mmmm,所以函数13()ln22hmmmm在1e],是单调增函数,…………………14分所以e3e1e3()(e)1022e2ehmh,故命题成立.…………………16分江苏省常州市北郊中学2011届高三上学期统一练习(数学)2.已知函数3log2xxxf(x>0),直线l与函数xf相切于点mA,1.则直线l的方程为.(写成直线方程一般式)012ln3)2(lnyx11.设)(xf是连续的偶函数,且当0x时是单调增函数,则满足)41()2(xxfxf的所有x之和为-8二、解答题20.已知函数555)(xxf,m为正整数(Ⅰ)求)0()1(ff和)1()(xfxf的值;(Ⅱ)若数列}{na的通项公式为)(mnfan(mn,,2,1),求数列}{na的前m项和mS;(Ⅲ)设数列}{nb满足:211b,nnnbbb21,设11111121nnbbbT,若(Ⅱ)中的mS满足对任意不小于3的正整数n,57774nmTS恒成立,试求m的最大值20.解:(Ⅰ)515555)0()1(ff=1;)1()(xfxf=5555551xx=xxx55555555=1;…………3分(Ⅱ)由(Ⅰ)得)11(1)1()(mkmkfmkf,即,11)()(kmkaa,mkmfmkf由m1m321maaaaaS,……………①得,aaaaaSm13m2m1mm…………②由①+②,得,21)1(2mmamS∴45521)1()1(21)1(mfmSm,…8分(Ⅲ)∵,211b)1b(bbbbnnn2n1n,∴对任意的0*,nbNn.∴,1b1b1)1b(b1b1nnnn1n即1nnnb1b11b1.∴111132211211)11()11()11(nnnnnbbbbbbbbbT.∵,bb,0bbbn1n2nn1n∴数列}b{n是单调递增数列.∴nT关于n递增.当3n,且Nn时,3TTn.∵256777)11621(1621,1621)143(43,43)121(21,214321bbbb∴.77725621243bTTn∴,577743TSm∴5.650m.而m为正整数,∴m的最大值为650.江苏省常州市武进区横山桥高级中学2011届高三上学期期中考试(数学理)7、若函数()4lnfxx,点(,)Pxy在曲线\'()yfx上运动,作PMx轴,垂足为M,则△POM(O为坐标原点)的周长的最小值为___▲___.8、已知32()\'(1)3\'(1)fxxxfxf,则\'(1)\'(1)ff的值为___▲___.11、已知||2||0ab,且关于x的函数3211()||32fxxaxabx在R上有极值,则a与b的夹角范围为___▲___.12、设函数()(01xxafxaa,且1)a,[]m表示不超过实数m的最大整数,则函数11[()][()]22fxfx的值域是___▲___.13、如图放置的边长为1的正三角形PAB沿x轴滚动.设顶点(,)Pxy的纵坐标与横坐标的函数关系式是()yfx,记()fx的最小正周期为T;()yfx在其两个相邻零点间的图象与x轴所围区域的面积记为S,则ST___▲___.二、解答题18、(本题满分16分)函数2219()()122fxxabx,2()gxaxb(abxR、、),集合2219{|310}22Axxx,(1)求集合A;(2)如果0b,对任意xA时,()0fx恒成立,求实数a的范围;(3)如果0b,当“()0fx对任意xA恒成立”与“()0gx在xA内必有解”同时成立时,求a的最大值.18、解:(1)令211xt,则221xt…………………………1分()0fx即219(1)3022tt即2680tt,(2)(4)0tt24t,…3分,所以2214x,所以[15,3][3,15]x,即[15,3][3,15]A………………………………5分(2)()0fx恒成立也就是2219()1022fxxax恒成立,2219122xax,即2219122axx,①+②可得22a所以a的最大值为22,此时322b.………………………16分19、(本题满分16分)函数(1)()ln(0,)axfxxxaRx.(1)试求()fx的单调区间;(2)当0a时,求证:函数()fx的图像存在唯一零点的充要条件是1a;(3)求证:不等式111ln12xx对于(1,2)x恒成立.19解:(1)/221()(0)axafxxxxx.……………………………………………2分 当0a时,/()0fx,在(0,)上单调递增;……………………………………3分 当0a时,(0,)xa时,/()0fx,在上单调递减;(,)xa时,/()0fx,在(,)a上单调递增.…………………………………5分综上所述,当0a时,的单调递增区间为(0,);当0a时,的单调递增区间为(,)a,单调递减区间为(0,)a.……6分(2)充分性:1a时,由(1)知,在1x处有极小值也是最小值,即min()(1)0fxf。而在(0,1)上单调递减,在(1,)上单调递增,在(0,)上由唯一的一个零点1x.……………………………………………………9分必要性:()0fx在(0,)上有唯一解,且0a,由(1)知,在xa处有极小值也是最小值()fa,()0fa,即ln10aa.∴(1)ln2(1)0xxx.∴111(12)ln12xxx.……………………16分20、(本题满分16分)对任意Rx,给定区间)](21,21[zkkk,设函数)(xf表示实数x与x的给定区间内整数之差的绝对值(1)当11[,]22x时,求出()fx的解析式;当11[,]()22xkkkz时,写出用绝对值符号表示的)(xf的解析式;(2)求44(),()33ff的值,判断函数()()fxxR的奇偶性,并证明你的结论;(3)当121ea时,求方程()log0afxx的实根.(要求说明理由1212e)20解:(1)当]21,21[x时,由定义知:x与0距离最近,||)(xxf,].21,21[x当)](21,21[Zkkkx时,由定义知:xk为与最近的一个整数,故11()||,[,]()22fxxkxkkkZ。…………………………3分(2)4141,3333ff…………………………4分判断()fx是偶函数…………………………5分对任何xR,函数)(xf都存在,且存在kZ,满足kkxkkxkkxxfkxk(21212121.||)(,2121可以得出由Z)即kkkx](21,21[Z).…………………………7分由(Ⅰ)的结论,()()||||(),fxxkkxxkfx…………………………9分即)(xf是偶函数.所以当)(,121xHx时为减函数,,0)1()(HxH所以方程没有121x的实根;……………………14分④当0log210log21||,210xxxkxxaa变为方程时设)(),210(log21)(xGxxxxGa明显为减函数,0)21()21()(HGxG,所以方程没有210x的实根.……………………15分综上可知,若121,()log0aeafxx方程有且仅有一个实根,实根为1.…16分江苏省常州市武进区横山桥高级中学2011届高三上学期期中考试(数学文)8、若函数()4lnfxx,点(,)Pxy在曲线\'()yfx上运动,作PMx轴,垂足为M,则△POM(O为坐标原点)的周长的最小值为___▲___.11、已知||2||0ab,且关于x的函数3211()||32fxxaxabx在R上有极值,则a与b的夹角范围为___▲___.13、如图放置的边长为1的正三角形PAB沿x轴滚动.设顶点(,)Pxy的纵坐标与横坐标的函数关系式是()yfx,则()fx的最小正周期为T;()yfx在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST=___▲___.江苏省成化高中2011届高三(上)期末模拟试卷〈三〉(必做题部分)10.已知函数)(xf定义在正整数集上,且对于任意的正整数x,都有(2)2(1)fxfx()fx,且(1)2,(3)6ff,则(2009)f.401814.已知函数①xxfln3)(;②xexfcos3)(;③xexf3)(;④xxfcos3)(.其中对于)(xf定义域内的任意一个自变量1x都存在唯一个自变量)()(,212xfxfx使=3成立的函数是序号是___③18.(本题满分16分)某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建筑面积为1000平方米,球场的总建筑面积的每平方米的平均建筑费用与球场数有关,当该球场建n个时,每平方米的平均建筑费用用f(n)表示,且f(n)=f(m)(1+20mn)(其中n>m,n∈N),又知建五座球场时,每平方米的平均建筑费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几个球场?18.解:设建成x个球场,则每平方米的购地费用为x1000101284=x1280由题意知f(5)=400, f(x)=f(5)(1+205x)=400(1+205x)从而每平方米的综合费用为y=f(x)+x1280=20(x+x64)+300≥20.264+300=620(元),当且仅当x=8时等号成立故当建成8座球场时,每平方米的综合费用最省.19.(本题满分16分).已知定义在R上的函数)3()(2axxxf,其中a为常数.(1)若x=1是函数)(xf的一个极值点,求a的值;(2)若函数)(xf在区间(-1,0)上是增函数,求a的取值范围;(3)若函数]2,0[),()()(xxfxfxg,在x=0处取得最大值,求正数a的取值范围.19.解:(I)).2(363)(,3)(223axxxaxxfxaxxf)(1xfx是的一个极值点,2,0)1(af;(II)①当a=0时,23)(xxf在区间(-1,0)上是增函数,0a符合题意;②当axxxfaxaxxfa2,0:0)(),2(3)(,021得令时;当a>0时,对任意0,0)(),0,1(axfx符合题意;当a<0时,当02,12,0)()0,2(aaxfax时符合题意;综上所述,.2a(III)].2,0[,6)33()(,023xxxaaxxga],2)1(2[36)33(23)(22xaaxxaaxxg令.044(*),02)1(2,0)(22axaaxxg显然有即设方程(*)的两个根为(*),,21由xx式得0221axx,不妨设210xx.当202x时,)(2xg为极小值,所以)(xg在[0,2]上的最大值只能为)0(g或)2(g;当22x时,由于)(xg在[0,2]上是单调递减函数,所以最大值为)0(g,所以在[0,2]上的最大值只能为)0(g或)2(g,又已知)(xg在x=0处取得最大值,所以),2()0(gg即].56,0(,0,56,24200aaaa所以又因为解得20.(本题满分16分)已知函数()fxkxm,当11,xab时,()fx的值域为22,ab,当22[,]xab时,()fx的值域为33[,]ab,依次类推,一般地,当11,nnxab时,()fx的值域为,nnab,其中k、m为常数,且110,1ab.(1)若k=1,求数列,nnab的通项公式;(2)若0k且1k,问是否存在常数m,使数列nb是公比不为1的等比数列?请说明理由;(3)若0k,设数列,nnab的前n项和分别为,nnST,求122008122008TTTSSS.20.解(1)因为()fxxm,当11[,]nnxab时,()fx为单调增函数,所以其值域为11[,]nnambm,于是*11,(,2)nnnnaambbmnnN.又a1=0,b1=1,所以(1)nanm,1(1)nbnm.(2)因为()(0)fxkxmk,当11[,]nnxab时,()fx为单调增函数,所以()fx的值域为11[,]nnkamkbm,所以*1(,2)nnbkbmnnN.要使数列{bn}为等比数列,11nnnbmkbb必须为与n无关的常数.又11,0,1bkk,故当且仅当0m时,数列nb是公比不为1的等比数列.(本题考生若先确定m=0,再证此时数列nb是公比不为1的等比数列,给全分)(3)因为0k,当11[,]nnxab时,()fx为单调减函数,所以()fx的值域为11[,]nnkbmkam,于是*11,(,2)nnnnakbmbkamnnN.所以211112211()()()()()()nnnnnnnnbakbakbakbak.111,1,()()1(),0,1.1iijiiijjjjikTSbakkkkk122008122008TTTSSS20082008111()()iiijjiijTSba200922017036,1,20082009,0,1.(1)kkkkkk江阴成化高中11届高三一调模拟试卷四13.给定(1)log(2)nnan(n∈N*),定义乘积12kaaa为整数的k(k∈N*)叫做“理想数”,则区间[1,2008]内的所有理想数的和为▲.答案:2026.讲评建议:换底公式:logloglogbabNNa.12lg(2)lg2kkaaa为整数,22mk,m∈N*.k分别可取23422,22,22,,最大值22m≤2008,m最大可取10,故和为22+23+…+210-18=2026.18、(本小题满分15分)已知函数()fx的导数2()33,fxxax(0).fb,ab为实数,12a.(Ⅰ)若()fx在区间[1,1]上的最小值、最大值分别为2、1,求a、b的值;(Ⅱ)在(Ⅰ)的条件下,求经过点(2,1)P且与曲线()fx相切的直线l的方程;(Ⅲ)设函数2()(()61)xFxfxxe,试判断函数()Fx的极值点个数.答案:解(Ⅰ)由已知得,323()2fxxaxb由()0fx,得10x,2xa.∵[1,1]x,12a,∴当[1,0)x时,()0fx,()fx递增;当(0,1]x时,()0fx,()fx递减.∴()fx在区间[1,1]上的最大值为(0)fb,∴1b.……………………………2分又33(1)11222faa,33(1)1122faa,∴(1)(1)ff.,即322a,得43a.故43a,1b为所求.………………………………4分(Ⅱ)解:由(1)得32()21fxxx,2()34fxxx,点(2,1)P在曲线()fx上.⑴当切点为(2,1)P时,切线l的斜率2()|4xkfx,∴l的方程为14(2)yx,即470xy.………………………………5分⑵当切点P不是切点时,设切点为00(,)Qxy0(2)x,切线l的斜率0200()|34xxkfxxx,∴l的方程为20000(34)()yyxxxx.又点(2,1)P在l上,∴200001(34)(2)yxxx,∴322000001(21)(34)(2)xxxxx,∴2200000(2)(34)(2)xxxxx,∴2200034xxx,即002(2)0xx,∴00x.∴切线l的方程为1y.…8分故所求切线l的方程为470xy或1y.………………………………9分(或者:由(1)知点A(0,1)为极大值点,所以曲线()fx的点A处的切线为1y,恰好经过点(2,1)P,符合题意.)(Ⅲ)解:2222()(3361)33(2)1xxFxxaxxexaxe.∴222()63(2)233(2)1xxFxxaexaxe22[66(3)83]xxaxae.………………………………11分二次函数266(3)83yxaxa的判别式为22236(3)24(83)12(31211)123(2)1aaaaa,令0,得:2133(2),22.333aa令0,得332,2.33aa或………………………………13分∵20xe,12a,∴当3223a-时,()0Fx,函数()Fx为单调递增,极值点个数为0;…14分当3123a时,此时方程()0Fx有两个不相等的实数根,根据极值点的定义,可知函数()Fx有两个极值点.………………………………16分江阴成化高中2011届高三第一次调研模拟试卷一7.已知函数log(3)ayax在[0,2)上是关于x的减函数,则实数a的取值范围为.3(1,]216.某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.(1)求该企业使用该设备x年的年平均污水处理费用y(万元);(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?16.解:(1)xxxy)2642(5.0100即5.1100xxy(0x);-----------------------------------7分(不注明定义域不扣分,或将定义域写成*Nx也行)(2)由均值不等式得:5.215.110025.1100xxxxy(万元)--------------11分当且仅当xx100,即10x时取到等号.----------------------13分答:该企业10年后需要重新更换新设备.----------14分20.已知函数)()0,1(),0()(xfyPtxtxxf作曲线过点的两条切线PM、PN,切点分别为M、N.(1)当2t时,求函数)(xf的单调递增区间;(2)设|MN|=)(tg,试求函数)(tg的表达式(3)在(2)的条件下,若对任意的正整数n,在区间]64,2[nn内,总存在m+1个数,,,,,121mmaaaa使得不等式)()()()(121mmagagagag成立,求m的最大值.20.解:(I)当,2)(,2xxxft时0221)(222xxxxf1分2,2xx或解得.则函数)(xf有单调递增区间为),2(),2,(4分(II)设M、N两点的横坐标分别为1x、2x,)1(.02).1)(1()(0),0,1().)(1()(:,1)(12112111121112ttxxxxtxtxPPMxxxtxtxyPMxtxf即有过点切线又的方程为切线同理,由切线PN也过点(1,0),得.02222ttxx(2)6分由(1)、(2),可得02,221ttxxxx是方程的两根,(*).22121txxtxx8分])1(1[)()()(||22122122211221xxtxxxtxxtxxxMN])1(1][4)[(22121221xxtxxxx把(*)式代入,得,2020||2ttMN因此,函数)0(2020)()(2ttttgtg的表达式为10分(III)易知]64,2[)(nntg在区间上为增函数,12121(2)()(1,2,,1).(2)()()().()()()(),immmggaimmggagagagagagagan则对一切正整数成立恒成立对一切的正整数不等式nnnggm)64()2(13分,)64(20)64(2022022022nnnnm.3136.3136]1616[61)]64()64[(61,1664)]64()64[(61222mnnnnnnnnnnnm恒成立对一切的正整数即由于m为正整数,6m.15分又当.,16,2,6121满足条件对所有的存在时naaaammm因此,m的最大值为6.江苏省成化高中2011届高三(上)期末模拟试卷〈二〉2.函数)1(log23xxy的定义域为 .1,24.设123)(aaxxf,a为常数.若存在)1,0(0x,使得0)(0xf,则实数a的取值范围是.1(,1)(,)218.某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为x01x,那么月平均销售量减少的百分率为2x.记改进工艺后,旅游部门销售该纪念品的月平均利润是y(元).(1)写出y与x的函数关系式;(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.18、(1)改进工艺后,每件产品的销售价为201x,月平均销售量为21ax件,则月平均利润2120115yaxx(元),∴y与x的函数关系式为235144yaxxx01x(2)由2542120yaxx得112x,23x(舍)当102x时0y;112x时0y,∴函数235144yaxxx01x在12x取得最大值.故改进工艺后,产品的销售价为1201230元时,旅游部门销售该纪念品的月平均利润最大.19.已知二次函数1)(2bxaxxf和函数bxabxxg21)(2,(1)若)(xf为偶函数,试判断)(xg的奇偶性;(5分)(2)若方程()gxx有两个不等的实根2121,xxxx,则①证明函数)(xf在(-1,1)上是单调函数;(6分)②若方程0)(xf的有两实根为4343,xxxx,求使4213xxxx成立的a的取值范围.(5分)19.解:(1)∵)(xf为偶函数,∴()()fxfx,∴0bx,∴0b∴21()gxax,∴函数()gx为奇函数;(2)①由xbxabxxg21)(2得方程(*)0122bxxa有不等实根∴△0422ab及0a得12ab即1122bbaa或又)(xf的对称轴1,12abx故)(xf在(-1,1)上是单调函数②21,xx是方程(*)的根,∴011212bxxa∴12121xabx,同理12222xabx∴)(1xf222211111axbxaxax212)(xaa同理)(2xf222)(xaa要使4213xxxx,只需0)(0)(021xfxfa即002aaa,∴1a或0)(0)(021xfxfa即002aaa,解集为故a的取值范围1a江苏省诚贤中学2011届高三数学试题7.已知函数)(xf是偶函数,且它在,0上是减函数,若)1()(lgfxf,则x的取值围是▲.10.若函数)2(xf=0),4lg(0),2sin(xxxx,则f(3+2)f(102)▲.119.(本小题满分16分)某工厂为了提高经济效益,决定花5600千元引进新技术,同时适当进行裁员.已知这家公司现有职工m人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.(1)若m=400时,要使公司利润至少增加10%,那么公司裁员人数应在什么范围内?(2)若20,mk且150,则1f(f())2=____________125.如果奇函数y=f(x)(x0),当x(0,+)时,f(x)=x1,则使f(x1)<0的x的取值范围是_________(-∞,0)∪(1,2)6.已知()||23fxxxax,若()fx在R上为增函数,则a的取值范围是_______[2,2]8.已知f(x)是以2为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数f(x)=kx+k+1(k∈R且k≠1)有4个零点,则k的取值范围是_____________1(,0)3东海高级中学2011届高三理科数学30分钟限时训练(09)2.若nmaa3log,2log,则nma2=.433.函数322aaxy是偶函数,且在(0,+∞)上是减函数,则整数a的取值为14.已知定义在R上的偶函数()fx满足(2)()1fxfx对于xR恒成立,且()0fx,则(119)f的值是______;19.已知3)2(cos32)2cos()2sin(2)(2xxxxf.(Ⅰ)化简f(x)的解析式;(Ⅱ)若0≤θ≤π,求θ,使函数f(x)为偶函数;(Ⅲ)在(Ⅱ)成立的条件下,求满足],[,1)(xxf的x的集合.9.(1)f(x)=))32sin(2)(()62cos(2xxfx或;(2)当6时,f(x)为偶函数(3)5{|}66xxx或东海高级中学2011届高三理科数学30分钟限时训练(10)2.若函数axxxf3)(3有3个不同的零点,则实数a的取值范围是(-2,2)3.已知函数)4(),1()4(,2)(xxfxxfx,那么)5(f=86.已知函数f(x)=mx+6在闭区间3,2上存在零点,则实数m的取值范围是.(-∞,-2]∪[3,+∞)8.设函数(),()fxxxbxcxR给出下列4个命题,所有正确命题的个数是.②①当0,0cb时,0)(xf只有一个实数根;②当0c时,)(xfy是偶函数;③函数)(xfy的图像关于点),0(c对称;④当0,0cb时,方程0)(xf有两个实数根。东海高级中学2011届高三理科数学30分钟限时训练(01)6.已知函数xbeaxxf)(图象上在点)2,1(P处的切线与直线xy3平行,则函数)(xf的解析式为_____.12.50.5xyxe东海高级中学2011届高三理科数学30分钟限时训练(03)1、函数xxy22的定义域为3,2,1,0,那么其值域为_____.0,1,39、已知函数()lnfxxax()aR.(Ⅰ)求函数()fx的单调区间;(Ⅱ)当a>0时,求函数()fx在[1,2]上最小值.解:(Ⅰ)1()fxax(0x),①当a≤0时,1()fxax>0,故函数()fx增函数,即函数()fx的单调增区间为(0,).②当0a时,令1()0fxax,可得1xa,当10xa时,1()0axfxx;当1xa时,1()0axfxx,故函数()fx的单调递增区间为1(0,]a,单调减区间是1[,)a.(Ⅱ)①当11a,即1a时,函数()fx在区间[1,2]上是减函数,∴()fx的最小值是(2)ln22fa. ②当12a,即12a时,函数()fx在区间[1,2]上是增函数,∴()fx的最小值是(1)fa.③当112a,即112a时,函数()fx在1[1,]a上是增函数,在1[,2]a是减函数.又(2)(1)ln2ffa,∴当1ln22a时,最小值是(1)fa;当ln21a时,最小值为(2)ln22fa. 综上可知,当0ln2a时,函数()fx的最小值是min()fxa;当ln2a时,函数()fx的最小值是min()ln2fx.东海高级中学2011届高三理科数学30分钟限时训练(04)6、已知函数xfy是定义在R上的偶函数,12xfxf对于Rx恒成立,且,0xf则119f.18、曲线xxyln在点(1,0)处的切线方程为.01yx3、已知直线kxy是xyln的切线,则k的值为.1e6、若函数32()31fxxax的图象与直线y=3只有一个公共点,则实数a的取值范围 .)1,1(9、已知定义在正实数集上的函数21()22fxxax,2()3lngxaxb,其中0a.设两曲线()yfx,()ygx有公共点,且在该点处的切线相同.(1)用a表示b,并求b的最大值;(2)求证:()()fxgx≥(0x).9解:(Ⅰ)设()yfx与()(0)ygxx在公共点00()xy,处的切线相同.()2fxxa∵,23()agxx,由题意00()()fxgx,00()()fxgx.即22000200123ln232xaxaxbaxax,,由20032axax得:0xa,或03xa(舍去).即有222221523ln3ln22baaaaaaa.令225()3ln(0)2httttt,则()2(13ln)httt.于是当(13ln)0tt,即130te时,()0ht;当(13ln)0tt,即13te时,()0ht.故()ht在130e,为增函数,在13e,∞为减函数,于是()ht在(0),∞的最大值为123332hee.(Ⅱ)设221()()()23ln(0)2Fxfxgxxaxaxbx,则()Fx23()(3)2(0)axaxaxaxxx.故()Fx在(0)a,为减函数,在()a,∞为增函数,于是函数()Fx在(0),∞上的最小值是000()()()()0FaFxfxgx.故当0x时,有()()0fxgx≥,即当0x时,()()fxgx≥.江苏省东海高级中学2011届高三上学期期中考试试题(数学)3、若1{1,0,,2}3,则使函数yx的定义域为R,且在(-∞,0)上单调递增的值为▲.316、已知二次函数()fx满足fxfx()()11,且ff()()0011,,若fx()在区间nm,上的值域是nm,,则m=▲,n=▲.m=0,n=110、已知函数6(3)3,7(),7xaxxfxax,数列na满足*(),nafnnN,且数列na是递增数列,则实数a的取值范围是▲.(2,3);12、已知函数)(xf的导数()(1)(),fxaxxa若()fx在xa处取到极大值,则a的取值范围是▲.1,013、函数()yfx是定义在R上的增函数,函数(2010)yfx的图象关于点(2010,0)对称.若实数,xy满足不等式22(6)(824)0fxxfyy,则22xy的取值范围是▲.(16,36)二、解答题20、(16分)已知函数||()2xmfx和函数()||28gxxxmm.(1)若2m,求函数()gx的单调区间;(2)若方程||()2mfx在[4,)x恒有唯一解,求实数m的取值范围;(3)若对任意1(,4]x,均存在2[4,)x,使得12()()fxgx成立,求实数m的取值范围.20、(1)2m时,2224(2)()24(2)xxxgxxxx,函数()gx的单调增区间为(,1),(2,),单调减区间为(1,2).…………4分(2)由||()2xmfx在[4,)x恒有唯一解,得xmm在[4,)x恒有唯一解.当xmm时,得0[4,)x;当xmm时,得2xm,则20m或24m,即20mm或.综上,m的取值范围是20mm或.…………10分(3)2()()2()xmmxxmfxxm,则()fx的值域应是()gx的值域的子集.①当84m时,()fx在(,4]上单调减,故4()(4)2mfxf,()gx在[4,]m上单调减,[,)m上单调增,故()()28gxgmm,所以4228mm,解得456mm或.②当8m时,()fx在(,4]上单调减,故4()(4)2mfxf,()gx在2,4m单调增,mm,2上单调减,[,)m上单调增,82)(164)4(mmgmg故()()28gxgmm,所以4228mm,解得456mm或.③04m时,()fx在(,]m上单调减,[,4]m上单调增,故()()1fxfm.()gx在[4,)上单调增,故()(4)82gxgm,所以821m,即742m.④0m时,()fx在(,]m上单调减,[,4]m上单调增,故()()1fxfm.()gx在[4,)上单调增,故()(4)82gxgm,所以821m,即72m.(舍去)综上,m的取值范围是7[,5][6,)2.…………16分江苏省东海高级中学2011届高三上学期周周练十(数学)2.已知函数lg(4)yx的定义域为A,集合{|}Bxxa,若P:“xA”是Q:“xB”的充分不必要条件,则实数a的取值范围▲.4a5.奇函数32()1fxaxbxcxx在处有极值,则3abc的值为▲ .08.函数xaxxf)(在[1,4]上单调递增,则实数a的最大值为▲.213.设函数2()3fxxaxa,()2gxaxa.若0Rx,使得0()0fx与0()0gx同时成立,则实数a的取值范围是▲.(7,+∞)17.(本题满分14分)某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)项目类别年固定成本每件产品成本每件产品销售价每年最多可生产的件数A产品20m10200B产品40818120其中年固定成本与年生产的件数无关,m为待定常数,其值由生产A产品的原材料价格决定,预计]8,6[m.另外,年销售x件B产品时需上交20.05x万美元的特别关税.假设生产出来的产品都能在当年销售出去.(1)写出该厂分别投资生产A、B两种产品的年利润12,yy与生产相应产品的件数x之间的函数关系并指明其定义域;(2)如何投资才可获得最大年利润?请你做出规划.17.解:(Ⅰ)设年销售量为x件,按利润的计算公式,有生产A、B两产品的年利润12,yy分别为:1102010200200yxmxmxx且xN………3分222184080.050.051040yxxxxx220.05100460,0120,.yxxxN……6分(Ⅱ)86m,010m,20)10(1xmy为增函数,0200,200xxNx又时,生产A产品有最大利润为10200201980200mm(万美元)……………………………………8分又220.05100460,0120,.yxxxN100x时,生产B产品有最大利润为460(万美元)10分作差比较:86.7,06.7,06.76,02001520460)2001980()()(max2max1mmmmmyy …12分所以:当6.76m时,投资生产A产品200件可获得最大年利润;当7.6m时,生产A产品与生产B产品均可获得最大年利润;当7.68m时,投资生产B产品100件可获得最大年利润.………14分19.(本题满分16分)已知函数.ln)(),()(2xxgRmmxxxf(1)记),()()(xgxfxh当1m时,求函数)(xh的单调区间;(2)若对任意有意义的x,不等式)()(xgxf恒成立,求m的取值范围;(3)求证:当1m时,方程)()(xgxf有两个不等的实根19.解:(1)当1m时,),0(ln)(2xxxxxh),0()12)(1(12112)(\'2xxxxxxxxxxh……3分当10x时,,0)(\'xh)(xh的单调减区间为);1,0(…………4分当1x时,,0)(\'xh)(xh的单调减区间为).,1(…………5分(2))()(xgxf等价于xmxxln2,其中,0xxxxxxxmlnln2…………6分令,ln)(xxxxt得,1ln)(\'22xxxxt…………7分当10x时,,0)(\'xt当1x时,,0)(\'xt1,1)1()(minmtxtm…………10分(3)设,ln)()()(2xmxxxgxfxh,其中.0x,01212)(\'22xmxxxmxxh等价于,0122mxx此方程有且只有一个正根为,4820mmx…………11分且当),0(0xx时,,0)(\'xh)(xh在),0(0x上单调递减;当),(0xx时,,0)(\'xh)(xh在),(0x上单调递增;函数只有一个极值.ln)()(00200minxmxxxhxh…………12分当1m时,,4820mmx关于m在),1(递增,.0ln),,1(00xx…………13分mmmmmm38,0)1(89)8(,12222,043848220mmmmmmx…………14分,0ln)(ln)()(00000200minxmxxxmxxxhxh………15分当1m时,方程)()(xgxf有两个不等的实根。………16分江苏省东海高级中学2011届高三上学期自主探究试题11(数学)7.在同一平面直角坐标系中,已知函数()yfx的图象与xye的图象关于直线yx对称,则函数()yfx对应的曲线在点(,()efe)处的切线方程为★.1yxeyxOPMQN11.已知函数bxaxxxf2331)((Rba,),若)(xfy在区间2,1上是单调减函数,则ba的最小值为★.2312.定义在)()()()(),0(xyfyfxfxf满足的函数,且0)(1xfx时,若不等式)()()(22afxyfyxf对任意),0(,yx恒成立,则实数a的取值范围为★.2,013.图为函数()(01)fxxx的图象,其在点(())Mtft,处的切线为l,l与y轴和直线1y分别交于点P、Q,点N(0,1),若△PQN的面积为b时的点M恰好有两个,则b的取值范围为★.18,42714.我们知道,如果定义在某区间上的函数()fx满足对该区间上的任意两个数1x、2x,总有不等式1212()()()22fxfxxxf成立,则称函数()fx为该区间上的向上凸函数(简称上凸).类比上述定义,对于数列na,如果对任意正整数n,总有不等式:212nnnaaa成立,则称数列na为向上凸数列(简称上凸数列).现有数列na满足如下两个条件:(1)数列na为上凸数列,且1101,28aa;(2)对正整数n(*,101Nnn),都有20nnab,其中2610nbnn.则数列na中的第五项5a的取值范围为★.13,2520.(16分)已知函数()2fxxxax.(1)若函数()fx在R上是增函数,求实数a的取值范围;(2)求所有的实数a,使得对任意[1,2]x时,函数()fx的图象恒在函数()21gxx图象的下方;(3)若存在[4,4]a,使得关于x的方程()()fxtfa有三个不相等的实数根,求实数t的取值范围.20.解:(1)22(2),,()2(2),,xaxxafxxxaxxaxxa≥由()fx在R上是增函数,则2,22,2aaaa≥≤即22a≤≤,则a范围为22a≤≤;…4分(2)由题意得对任意的实数[1,2]x,()()fxgx恒成立,即1xxa,当[1,2]x恒成立,即1xax,11xaxx,11xaxxx,故只要1xax且1axx在[1,2]x上恒成立即可,在[1,2]x时,只要1xx的最大值小于a且1xx的最小值大于a即可,………6分而当[1,2]x时,21110xxx,1xx为增函数,max132xx;当[1,2]x时,21110xxx,1xx为增函数,min12xx,所以322a;…………………10分(3)当22a≤≤时,()fx在R上是增函数,则关于x的方程()()fxtfa不可能有三个不等的实数根;………11分则当(2,4]a时,由22(2),,()(2),xaxxafxxaxxa≥得xa≥时,2()(2)fxxax对称轴22axa,则()fx在[,)xa为增函数,此时()fx的值域为[(),)[2,)faa,xa时,2()(2)fxxax对称轴22axa,则()fx在2,2ax为增函数,此时()fx的值域为2(2),4a,()fx在2,2axa为减函数,此时()fx的值域为2(2)2,4aa;由存在(2,4]a,方程()()2fxtfata有三个不相等的实根,则2(2)22,4ataa,即存在(2,4]a,使得2(2)1,8ata即可,令2(2)14()488agaaaa,只要使max()tga即可,而()ga在(2,4]a上是增函数,max9()(4)8gag,故实数t的取值范围为91,8;…………………15分同理可求当[4,2)a时,t的取值范围为91,8;综上所述,实数t的取值范围为91,8.……………16分江苏省东海县高级中学2011届高三理科数学练习十三17.已知某企业原由工人500人,每人每年可为企业创利润6万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗,为维护生产稳定,该企业决定待岗人数不超过原有工人的10%,并且每年给每位待岗工人发放生活补贴0.5万元。据评估,当待岗工人的人数x不超过原有工人数的5%时,留岗工人每人每年可为企业多创利润9110x万元,当待岗员工人数x超过原有员工的5%,时,留岗员工每人每年可为企业多创利润1万元.(1)试用x表示企业年利润y的函数关系式;(2)为使企业年利润y最大,求应安排多少工人待岗?17.解:(1)9(500)(7)0.510(500)70.52650xxyxxxx 1x25 ,xN(2)当8x时,年利润y最大,即为使企业年利润y最大,则应安排8名工人待岗!江苏省东海县高级中学2011届高三上学期练习十四(数学理)4.设xR,函数2lg(43)ymxmxm有意义,实数m取值范围.[0,1)14.函数()fx满足1(0,1)1()xaaafx,若12()()1fxfx,则12()fxx的最大值为.5419.已知ln(),0()ln0,axxxefxaxxxe,函数,,其中a为常数.(1)试判断函数f(x)的奇偶性;(2)若(0,]e时,函数()fx的最大值为1,求实数a的值.(3)在(2)的条件下,求证:11ln(1)()ninnNn19.解:(1)当,0xe时,则0,xe∴()()ln(x)ln()f(x)fxaxaxx---------------2分0,xe当时,则,0xe∴()()lnxln(ln)f(x)fxaxaxxaxx-----------4分∴函数f(x)为奇函数---------------5分(2)假设存在满足条件的实数a1()fxax,---------------6分①1ae当时,由于0,xe,1()0fxax∴()fx在0,xe上是增函数min()()11fxfeae21aee,(舍去)---------------8分②1ae当时,令1()0,fxxa得则()fx1,ea在上递减,)1(0,-a上递增max11()()1ln()1fxfaa,解得1a综合①②可知1a---------------11分(3)由(2)知,()ln1fxxx,0,xe∴ln1xx(当且仅当1x时取“=”)-------13分∵111en∴11ln(1)nn-------14分NMPFEDCBA(第17题图)∴111341ln(1)ln(1)ln(1)ln2lnlnln1223nnn=341111ln(2)ln(1)2312nnnn∴11ln(1)()ninnNn-------16分江苏省东海县高级中学2011届高三上学期练习十五(数学理)4.0.34121,log3log5,,,2abcabc若,则的大小关系为(),则cba,,的大小关系为__________________.(用<表示)cba5.若21()ln(2)2fxxbx在(-1,+)上是减函数,则实数b的取值范围是______________.1b6.右图是函数2()fxxaxb的部分图象,则函数/()ln()gxxfx的零点所在的区间是________________.③①11(,)42②(1,2)③1(,1)2④(2,3)10.设22,2()log(1)2xttxfxxx且(2)1,f则((5))ff的值为________.811.曲线xey21在点),4(2e处的切线方程为____________________.22220exye13.已知定义在R上的偶函数()fx满足(2)()1fxfx对于xR恒成立,且()0fx,则(119)f________;114.四位同学在研究函数)(1)(Rxxxxf时,分别给出下面四个结论:①函数)(xf的图象关于y轴对称;②函数)(xf的值域为(-1,1);③若,21xx则一定有)()(21xfxf;④若规定)()(1xfxf,)]([)(1xffxfnn,则xnxxfn1)(对任意*Nn恒成立.你认为上述四个结论中正确的有②③④16.已知下列两个命题::P函数)(42)(2Rmmxxxf在),2[单调递增;:Q关于x的不等式244(2)10xmx)(Rm的解集为R;若PQ为真命题,PQ为假命题,求m的取值范围.16解:函数)(42)(2Rmmxxxf的对称轴为mx故P为真命题2m 2[4(2)]441013.Qmm为真命题,,.PQPQPQ为真为假与一真一假若假真QP,则2m,且31mm或,1m若真假QP,则2m,且31m,32m综上所述,m的取值范围321mmm或17.如图,ABCD是正方形空地,边长为30米,电源在点P处,点P到边,ADAB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,:16:9MNNE.线段MN必须过点P,端点,MN分别在边,ADAB上,设ANx米,液晶广告屏幕MNEF的面积为S平方米.(1)求S关于的函数关系式及该函数的定义域;(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?17.解:(1)39xAMx(1030)x≤≤.2222229(9)xMNANAMxx.∵:16:9MNNE,∴916NEMN.∴2222999[]1616(9)xSMNNEMNxx.……5分定义域为[10,30].(3)224918(9)9(218)[2]16(9)xxxxSxx=339[(9)81]8(9)xxx,令0S,得0x(舍),3933x.当310933x≤时,0,SS关于x为减函数;当393330x≤时,0,SS关于x为增函数;∴当3933x时,S取得最小值.答:当AN长为3933m时,液晶广告屏幕MNEF的面积S最小.19.设函数xbxxfln)1()(2,其中b为常数.(1)当21b时,判断函数()fx在定义域上的单调性;(2)若函数()fx的有极值点,求b的取值范围及()fx的极值点;(3)求证对任意不小于3的正整数n,不等式nnnn1ln)1ln(12都成立.19.解:(1)由题意知,()fx的定义域为),0(,)0(21)21(22222)(\'22xxbxxbxxxbxxf……1分当21b时,()0fx,函数()fx在定义域),0(上单调递增.……2分(2)设bxxxG22)(2,若函数()fx的有极值点,则G(x)=0有解21;08-4bb当12b时,()0fx有两个不同解,221211bx22121,2bx………4分0)bi时,,舍去),0(0221211bx,),0(1221212bx而,此时()fx,()fx随x在定义域上的变化情况如下表:x),0(2x2x2()x,()fx0()fx减极小值增由此表可知:0b时,()fx有惟一极小值点22121,bx,……6分ii)当102b时,0<21xx<1此时,()fx,()fx随x的变化情况如下表:x10x,1x12()xx,2x2()x,()fx00()fx增极大值减极小值增()fx有极大值221211bx和极小值点221212bx;……8分综上所述:当且仅当21b时()fx有极值点;当0b时,()fx有惟一最小值点22121,bx;当102b时,()fx有一个极大值点22121bx和一个极小值点22121bx……9分(3)由(2)可知当1b时,函数xxxfln)1()(2,此时()fx有惟一极小值点23122121bx为减函数在时,)231,0()(,0)(\')231,0(xfxfx成立时恒有当,即恒有恒有,时,当1ln)1ln(3)11ln(10)11(f(1)231341110322nnnnnnnfnn令函数)0ln)1()(xxxxh(xxxxh111)(\'则2!1\'()0()1[1,)()!!1111311(1)(1)ln(1)0n11ln(1)lnln(1)113ln(1)lnnxhxhxxxhxrnrnhhnnnnnnnnnnnn时,,又在处连续时为增函数时即综上述可知时恒有20.已知函数2,mxfxmnRxn在1x处取得极值2,(1)求fx的解析式;(2)设A是曲线yfx上除原点O外的任意一点,过OA的中点且垂直于x轴的直线交曲线于点B,试问:是否存在这样的点A,使得曲线在点B处的切线与OA平行?若存在,求出点A的坐标;若不存在,说明理由;(3)设函数22gxxaxa,若对于任意1xR的,总存在21,1x,使得21gxfx,求实数a的取值范围。20、(I).………2分又fx在1x处取得极值2.22(1)01040(1)(11122,141mnfmmnnnfmnxfxx即解得或舍去)………………4分(Ⅱ)由(I)得222441xfxx假设存在满足条件的点A,且00204,1xAxx,则2041OAkx………………6分20200222200204200022200200044164224121644,,54214420,,555OAxxxfxxxxkfxxxxxxx依题意得即………………8分江苏省东海县高级中学2010-2011学年度第一学期期中考试高三理科数学试题3.奇函数32()1fxaxbxcxx在处有极值,则3abc的值为 ▲ .011.已知函数2240()04xxxfxxxx,,,若2(8)(2)fafa,则实数a的取值范围是____▲__.(42),13.已知函数1()||(0)fxxaxx,若1()2fx恒成立,则实数a的取值范围是_____▲______.620.(本小题满分16分)已知函数()ln()(xfxeaa为常数)是实数集R上的奇函数,函数()()singxfxx是区间[-1,1]上的减函数.(1)求a的值;(2)若2()1gxtt在[1,1]x上恒成立,求实数t的取值范围;(3)设mR,讨论关于x的方程2ln(2)()xxexmfx的根的个数.20.解:(1)2()ln(),ln()ln(),()()1,11,()004.xxxxxxxxxfxeaeaeaeaeaaeaeaaeeaa+是奇函数则恒成立整理得分(2)因为/()sin[-1,1],()cos0[-1,1]gxxxgxx在上是减函数在上恒成立,又cos,cos[cos1,1],1.xx………………………6分又max()[-1,1],()(1)sin1,gxgxg在上是减函数所以只需2sin11tt,2(1)sin110(-1)tt其中恒成立.令2()(1)sin11(1)htt,则210(1)sin110ttt1t--10分.(3)由(1)知()fxx,所以方程化为:2ln(2)xxexmx22/1212lnln1ln2,(),()2,()xxxxexmfxfxxexmfxxxx令//111(0,),()0,()(0,],[,),()0xefxfxexefx当时即在上是增函数当即1()[,)fxe在是减函数,所以当xe时,1max11()()fxfee,而222()()fxxeme,即22min2()()fxfeme,结合图象知22222211,,11,,11,,.memeeememeeememeee当时即时方程无解;当时即时方程有一解;当时即时方程有个解…………16分.江苏省东海县高级中学2010-2011学年度第一学期期中考试高三数学试题(文科)5.已知0,1)1(0,cos)(xxfxxxf,则4()3f的值为____▲______.327.已知2()3(2),(2)fxxxff则=▲.-214.已知函数()()1||xfxxRx时,则下列结论不正确的是▲(4)(1).xR,等式()()0fxfx恒成立(2).(0,1)m,使得方程|()|fxm有两个不等实数根(3).12,xxR,若12xx,则一定有12()()fxfx(4).(1,)k,使得函数()()gxfxkx在R上有三个零点18.(本题满分16分)某水库堤坝因年久失修,发生了渗水现象,当发现时已有200m2的坝面渗水.经测算知渗水现象正在以每天4m2的速度扩散.当地政府积极组织工人进行抢修.已知每个工人平均每天可抢修渗水面积2m2,每人每天所消耗的维修材料费75元,劳务费50元,给每人发放50元的服装补贴,每渗水1m2的损失为250元.现在共派去x名工人,抢修完成共用n天.(Ⅰ)写出n关于x的函数关系式;(Ⅱ)要使总损失最小,应派去多少名工人去抢修(总损失=渗水损失+政府支出).18.解:(Ⅰ)由题意得22004nxn所以100,3,2nxxNx.……………4分(Ⅱ)设总损失为,12550250262550yynxxnxnxx………8分当且仅当时,即时,等号成立.………………………14分所以应派52名工人去抢修,总损失最小.………………………16分19.(本题满分16分)已知函数()lnfxx,()(0)agxax,设()()()Fxfxgx.(Ⅰ)求函数()Fx的单调区间;(Ⅱ)若以函数()((0,3])yFxx图像上任意一点00(,)Pxy为切点的切线的斜率12k恒成立,求实数a的最小值;(Ⅲ)是否存在实数m,使得函数2211aygmx的图像与函数2(1)yfx的图像恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由。19.解:(I)ln0aFxfxgxxxx,221\'0axaFxxxxx∵0a,由\'0,Fxxa,∴Fx在,a上单调递增。由\'00,Fxxa,∴Fx在0,a上单调递减。∴Fx的单调递减区间为0,a,单调递增区间为,a……………4分(II)2\'03xaFxxx,000201\'032xakFxxx恒成立200max12axx当01x时,20012xx取得最大值12………………………8分∴12a,∴min12a………………………10分(III)若222111122aygmxmx的图象与221ln1yfxx的图象恰有四个不同得交点,即2211ln122xmx有四个不同的根,亦即2211ln122mxx有四个不同的根。令2211ln122Gxxx,则32221122\'111xxxxxxxGxxxxx………………………12分当x变化时,\'Gx、Gx的变化情况如下表:x(,1)(1,0)(0,1)1,\'Gx的符号+-+-Gx的单调性由表格知:1()(0)2GxG极小值,11ln20GxGG极大值………14分画出草图和验证1122ln5222GG可知,当1,ln22m时,yGx与ym恰有四个不同的交点。∴当1,ln22m时,222111122aygmxmx的图象与221ln1yfxx的图象恰有四个不同的交点。……………………………16分江苏省高淳高级中学2011届高三上学期第二次质量检测(数学理)11.若函数f(x)=x2lga-2x+2在区间(1,2)内有且只有一个零点,那么实数a的取值范围是_____▲______.(1,)14.已知f(x)=ax2+bx+c(a≠0),且方程f(x)=x无实数根,下列命题:①方程f[f(x)]=x也一定没有实数根;②若a>0,则不等式f[f(x)]>x对一切实数x都成立;③若a<0,则一定存在实数x0,使f[f(x0)]>x0;④若a+b+c=0,则不等式f[f(x)]<x对一切实数x都成立.其中正确命题的序号是________▲______①②④(把你认为正确的命题的所有序号都填上).17.(本小题满分14分)某公司为了加大产品的宣传力度,准备立一块广告牌,在其背面制作一个形如△ABC的支架,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米.为节省材料,要求AC的长度越短越好,求AC的最短长度,且当AC最短时,BC的长度为多少米?17.14.设BC=x米(x>1),AC=y米,则AB=y-.……2分在△ABC中,由余弦定理,得(y-)2=y2+x2-2xycos60.……4分所以y=(x>1).……7分法一:y==(x-1)++2≥2+.当且仅当x-1=,即x=1+时,y有最小值2+.……12分法二:y′==.由y′=0得x=1+.因为当1<x<1+时,y′<0;当x>1+时,y′>0,所以当x=1+时,y有最小值2+.……12分答:AC的最短长度为2+米,此时BC的长度为(1+)米.……14分20.(本小题满分16分)BCA已知函数f(x)=x-a-lnx.(Ⅰ)若a=1,求f(x)的单调区间及f(x)的最小值;(Ⅱ)若a>0,求f(x)的单调区间;(Ⅲ)试比较++…+与(n∈N*且n≥2)的大小,并证明你的结论.20.(1)1,()1lnafxxx111,()1ln,()10.xxfxxxfxxx当时()1,.fx在区间上是递增的……………2分101,()1ln,()10xfxxxfxx当()(0,1).fx在区间上是递减的故a=1时,()fx的增区间为[1,),减区间为(0,1),min()(1)0.fxf………4分(2)若111,()ln,()10.xaxafxxaxfxxx当时,则()fx在区间[,]a上是递增的;当10,()ln,()10xafxaxxfxx时()fx在区间(0,)a上是递减的.………6分若01,,()ln,axafxxax当时11()1,1,()0,1,()0xfxxfxaxfxxx则()fx在区间[1,)上是递增的,()fx在区间[,1)a上是递减的;当10,()ln,()10,xafxaxxfxx时()fx在区间(0,a)上是递减的,而()fx在xa处连续;则()fx在区间[1,)上是递增的,在区间(0,1)上是递减的综上:当1,()afx时的递增区间是[,)a,递减区间是(0,a);当01a时,()fx的递增区间是[1,),递减区间是(0,1)…………11分(3)由(1)可知,当1a,1x时,有1ln0xx,即ln11xxx222222ln2ln3ln23nn22211111123n2221111()23nn……13分1111111()23341nnn11(1)(21)1()212(1)nnnnn…………………16分江苏省海安、如皋2011届高三上学期期中考试试卷(数学理)9.若函数2()5fxmxx在2),上是增函数,则m的取值范围是▲.104,11.若关于x的方程kx-lnx=0有解,则k的取值范围是▲.1e,13.设()fx是定义在2,上的减函数,且22(sin1)(cos)faxfax≤对一切xR都成立,则a的取值范围是▲.11022,14.设函数22fxxxbxc,则下列命题中正确命题的序号是▲.①③⑤①当0b时,fx在R上有最大值;②函数fx的图象关于点0c,对称;③方程fx=0可能有4个实根;④当0b时,fx在R上无最大值;⑤一定存在实数a,使fx在[)a,上单调递减.17.(本题满分14分)定义在R上的奇函数()fx有最小正周期2,且当(01)x,时,()22xxfx.(1)求()fx在[-1,0)上的解析式;(2)判断()fx在(-2,-1)上的单调性,并给予证明.【解】(1)因为奇函数()fx的定义域为R,周期为2,所以(1)(12)(1)fff,且(1)(1)ff,于是(1)0.f……………………2分当(10)x,时,(01)x,,()()2222xxxxfxfx. …………………………5分所以()fx在[-1,0)上的解析式为0(1)()22(10).xxxfxx,,,……………………7分(2)()fx在(-2,-1)上是单调增函数.…………………………9分先讨论()fx在(0,1)上的单调性.[方法1]设1201xx,则11221212121()()22222212xxxxxxxxfxfx因为1201xx,所以12122221xxxx,,于是12121220102xxxx,,从而12()()0fxfx,所以()fx在(0,1)上是单调增函数. ………………………12分因为()fx的周期为2,所以()fx在(-2,-1)上亦为单调增函数.………………14分[方法2]当(01)x,时,()22ln2xxfx.因为ln2>0,220xx,所以()22ln20xxfx,所以()fx在(0,1)上是单调增函数.………………………12分因为()fx的周期为2,所以()fx在(-2,-1)上亦为单调增函数.………………14分【注】第(2)小题亦可利用周期性求出22()22(21)xxfxx,再利用定义或导数确定单调性.江苏省海安、如皋2011届高三上学期期中考试试卷(数学文)11.若正数a,b,c满足a2+2ab+4bc+2ca=16,则a+b+c的最小值是▲.417.(本题满分14分)已知函数21(0)()21(1)xccxxcfxcx,,,≤满足29()8fc.(1)求常数c的值;(2)解不等式2()18fx.【解】(1)由题意知0
展开内容










 2022-2023学年江西省南昌市西湖区名校联盟七年级(下册)期中数学试卷word
2022-2023学年江西省南昌市西湖区名校联盟七年级(下册)期中数学试卷word 2020年高考真题数学(文科)(全国卷Ⅰ)+答案解析
2020年高考真题数学(文科)(全国卷Ⅰ)+答案解析 2017年北京高考数学(理科)试题试卷+答案(word版)
2017年北京高考数学(理科)试题试卷+答案(word版)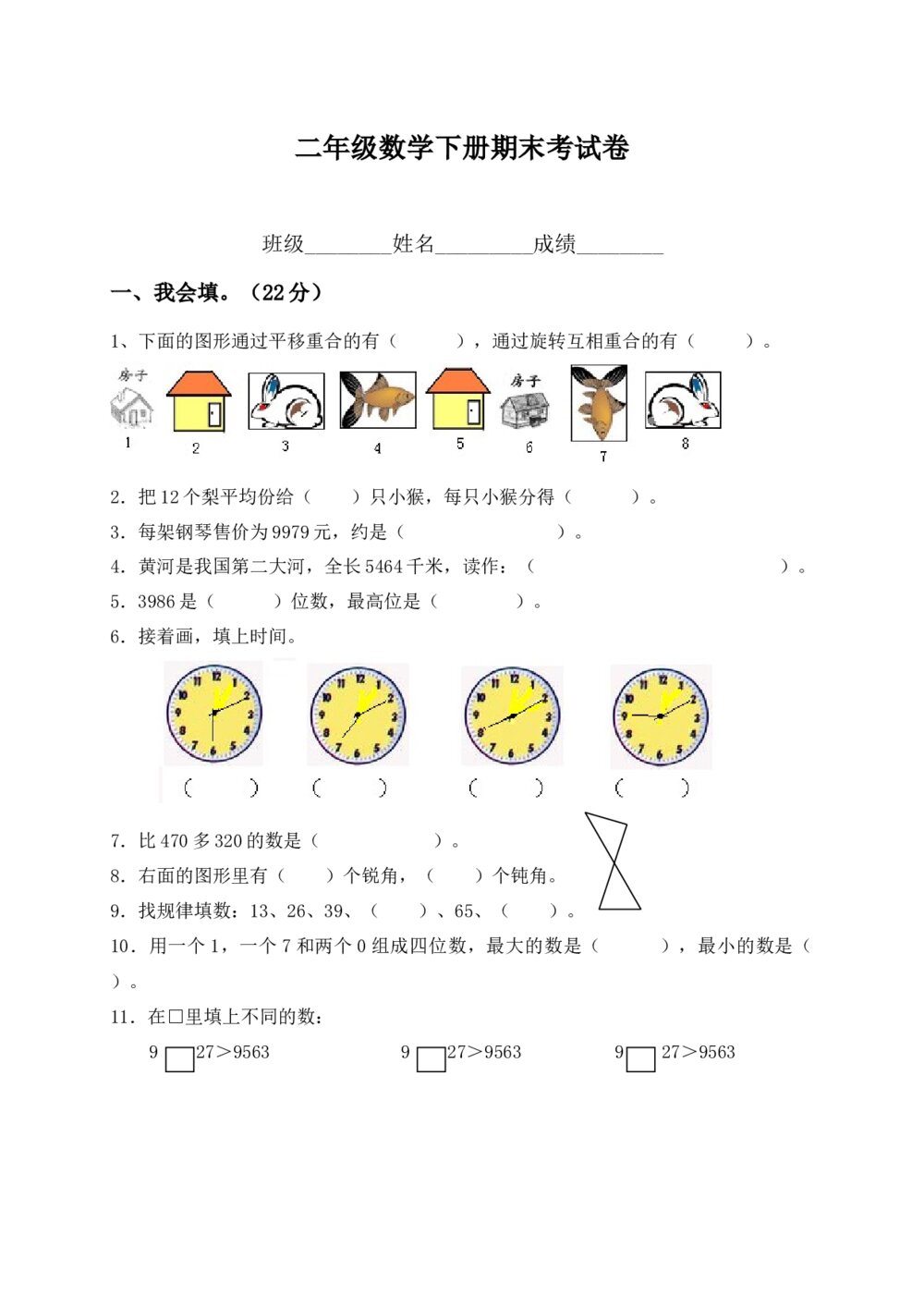 二年级数学下册期末考试卷word版
二年级数学下册期末考试卷word版 2011浙江省高考理科综合能力测试卷
2011浙江省高考理科综合能力测试卷 2013年北京高考(文科)数学试题试卷+答案
2013年北京高考(文科)数学试题试卷+答案