









试读已结束,还剩2页未读,您可下载完整版后进行离线阅读
《2012年石家庄市高三二模数学试卷+答案(文科)》是由用户上传到老师板报网,本为文库资料,大小为634.5 KB,总共有12页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 12页
- 634.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2012年石家庄市高中毕业班第二次模拟考试高三数学(文科)注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第I卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3.回答第II卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第I卷(选择题60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={5,6,7},N={5,7,8},则A.B.C.D.=(6,7,8}2.复数-(i为虚数单位)在复平面内对应的点所在的象限为A.第一象限B.第二象限C.第三象限D.第四象限3.已知函数分别由右表给出,则的值为A.1B.2C.3D.44.若x、y满足约束条件,则z=3x-yA.最小值-8,最大值0B.最小值-4,最大值0C.有最小值-4,无最大值D.有最大值-4,无最小值5.的值为A.1B.C.D.6.已知向量a=(1,2),b=(2,3),则是向量与向量n=(3,-1)夹角为钝角的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要的条件7.一个几何体的正视图与侧视图相同,均为右图所示,则其俯视图可能是8.程序框图如右图,若n=5,则输出的s值为A.30B.50C.62D.669.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:根据上表可得回归直线方程,据此模型预报身高为172cm的高三男生的体重为A.70.09B.70.12C.70.55D.71.0510.已知拋物线的焦点为F,点M在该拋物线上,且在x轴上方,直线的倾斜角为600,则|FM|=A.4B.6C.8D.1011.已知a是实数,则函数的图象不可能是12.已知函数则满足不等式的%的取值范围为A.B.(-3,1)C.[-3,0)D.(-3,0)第II卷(非选择题共90分)本卷包括必考题和选考题两部分,第13题〜第21题为必考题,每个试题考生都必须作答.第22题〜第24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.13.双曲线的离心率为________.14.在中,,AC=1,AB=,则BC的长度为________.15.在区间[1,3]上随机选取一个数x,ex(e为自然对数的底数)的值介于e到e2之间的概率为________.16.已知长方体ABCE-A1B1C1D1的外接球的体积为36,则该长方体的表面积的最大值为________.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知等比数列{an}的前n项和为Sn,a1=2,S12S23S3成等差数列.(I)求数列{an}的通项公式;(II)数列是首项为-6,公差为2的等差数列,求数列{bn}的前n项和.18.(本小题满分12分)在三棱柱中,侧面为矩形,AB=1,,D为的中点,BD与交于点0,CO丄侧面(I)证明=BCAB1(II)若OC=OA,求三棱锥的体积.19.(本小题满分12分)我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了100位居民某年的月均用水量(单位:t),制作了频率分布直方图.(I)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;(II)用样本估计总体,如果希望80%的居民每月的用水量不超出标准〜则月均用水量的最低标准定为多少吨,请说明理由;(III)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).20.(本小题满分12分)已知点P(l,)在椭圆上,且该椭圆的离心率为.(I)求椭圆E的方程;(II)过椭圆E上一点P(x0,3)作圆的两条切线,分别交x轴于点B、C,求的面积.21.(本小题满分12分)己知函数(a<2,e为自然对数的底数).(1)若a=1,求曲线在点处的切线方程;(II)若存在,使得.,求实数a的取值范围.请考生在第22〜24三题中任选一题做答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-1几何证明选讲已知四边形ACBE,AB交CE于D点,(I)求证:;(II)求证:A、E、B、C四点共圆.23.(本小题满分H)分)选修4-4坐标系与参数方程在平面直角坐标系经xOy中,以0为极点,x轴的正半轴为极轴,取与直角坐标系相同的长度单位建立极坐标系.曲线C1的参数方程为:(为参数);射线C2的极坐标方程为:,且射线C2与曲线C1的交点的横坐标为.(I)求曲线C1的普通方程;(II)设A、B为曲线C1与y轴的两个交点,M为曲线C1上不同于A、B的任意一点,若直线MA与MB分别与x轴交于P、Q两点,求证|OP|•|OQ|为定值.24.(本小题满分10分)选修4-5不等式选讲设函数..(I)画出函数y=f(x)的图象;(II)若不等式恒成立,求实数a的取值范围.2012年石家庄市高中毕业班第二次模拟考试高三数学(文科答案)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1-5CBACB6-10ABCBC11-12BD二、填空题:本大题共4小题,每小题5分,共20分.13.5414.1或215.1216.72三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.解:(Ⅰ)由已知21343SSS,211114()3(1)aaqaaqq………………….2分230qq,0q(舍)或13q……………………4分1123nna.………………………….6分(Ⅱ)由题意得:28nnban,.........................8分11282283nnnbann,设数列nb的前n项和为nT.nn121-3n(-6+2n-8)T=+121-3…………………….10分121733nnn.……………………….12分18.解:(Ⅰ)因为11ABBA是矩形,D为1AA中点,1AB,12AA,22AD,所以在直角三角形1ABB中,112tan2ABABBBB,在直角三角形ABD中,12tan2ADABDAB,所以1ABB=ABD,…………………2分又1190BABABB,190BABABD,所以在直角三角形ABO中,故90BOA,即1BDAB,…………………………………………………………………………4分又因为11COABBA侧面,111ABABBA侧面,所以1COAB所以,1ABBCD面,BCBCD面,故1BCAB………………………6分(Ⅱ)在RtABD中,可求得62BD,2132362ADABOCOABD111222ABBSABBB…………………………9分111--11236332318BABCCABBABBVVSOC…………………………12分19.解:(Ⅰ)……………………………………………………………………3分(Ⅱ)月均用水量的最低标准应定为2.5吨.样本中月均用水量不低于2.5吨的居民有20位,占样本总体的20%,由样本估计总体,要保证80%的居民每月的用水量不超出标准,月均用水量的最低标准应定为2.5吨.………………………………………………7分(Ⅲ)这100位居民的月均用水量的平均数为1357911130.5(0.100.200.300.400.600.30.1)44444441.875…………………12分20.解:(Ⅰ)依题意得:222221245141ceaabcab,…………………2分解之得4,2,23acb.∴椭圆E的方程为2211612xy.………………5分(Ⅱ)把0(,3)Px代入2211612xy,求得02x,不妨取02x,易知过椭圆E上一点0(,3)Px作圆22(1)1xy的两条切线的斜率存在,设为k,则切线的方程为:3(2)ykx,………………7分依题意得22211kk,化简得23830kk,则147,3k2473k.∴切线的方程为:473(2)3yx,…………………9分令0y得27Bx,27Cx∴1273372PBCS.…………………12分21.解:(Ⅰ)当1a时,2()(1)xfxxxe,切点为(1,)e,于是有2()()xfxxxe,……………2分(1)2kfe∴ 切线方程为2yexe.………………5分(Ⅱ)()(2)xfxxxae,令()0fx,得20xa 或 0x,(1)当220a„,即02a„时,x2(2,2)a2a(2,0)a0(0,2)2()fx+0_0+()fx极大值极小值∴ 2(2)(4)afaea,2(2)(4)fea,当02a„时,有(2)(2)ffa…若存在[2,2]x使得22()3fxae…,只须222(4)3eaae…,解得413a„„, ∴ 01a„„.……………8分②当22a,即0a时,x2(2,0)0(0,2)2()fx-0+()fx极小值∴ 2(2)(43)fea,2(2)(4)fea,∵ 22(43)(4)eaea, ∴ (2)(2)ff若存在[2,2]x使得22()3fxae…,只须222(4)3eaae…,解得413a„„, ∴ 403a„.……………11分综上所述 413a„„.………………12分请考生在第22~24三题中任选一题做答,如果多做,则按所做的第一题记分22.(本小题满分10分)选修4-1几何证明选讲证明:(Ⅰ)依题意,DEBEBEEC,11,所以DEBBEC,………………2分得34,因为45,所以35,又26,可得EBDACD.……………………5分(Ⅱ)因为因为EBDACD,所以EDBDADCD,即EDADBDCD,又ADECDB,ADECDB,所以48,………………7分因为0123180,因为278,即274,由(Ⅰ)知35,所以01745180,即0180,ACBAEB所以A、E、B、C四点共圆.………………10分23.(本小题满分10分)选修4-4:坐标系与参数方程解:(Ⅰ)曲线1C的普通方程为2221xya,射线2C的直角坐标方程为(0)yxx,…………………3分可知它们的交点为66,33,代入曲线1C的普通方程可求得22a.所以曲线1C的普通方程为2212xy.………………5分(Ⅱ)||||OPOQ为定值.由(Ⅰ)可知曲线1C为椭圆,不妨设A为椭圆1C的上顶点,设(2cos,sin)M,(,0)PPx,(,0)QQx,因为直线MA与MB分别与x轴交于P、Q两点,所以AMAPKK,BMBQKK,………………7分由斜率公式并计算得2cos1sinPx,2cos1sinQx,所以||||2PQOPOQxx.可得||||OPOQ为定值.……………10分24.(本小题满分10分)选修4-5:不等式选讲解:(Ⅰ)由于37,2,()352.xxfxxx…………2分则函数的图象如图所示:(图略)……………5分(Ⅱ)由函数()yfx与函数yax的图象可知,当且仅当132a时,函数yax的图象与函数()yfx图象没有交点,……………7分所以不等式()fxax恒成立,则a的取值范围为1,32.…………………10分










 高考文科数学二轮复习《专题1集合与常用逻辑用语、函数、不等式》PPT版
高考文科数学二轮复习《专题1集合与常用逻辑用语、函数、不等式》PPT版 江苏省南通市2012届高三数学试卷+参考答案
江苏省南通市2012届高三数学试卷+参考答案 2016年江苏省高考(文科)数学试卷word版+答案
2016年江苏省高考(文科)数学试卷word版+答案 2012广东省高考数学(文科)试题试卷
2012广东省高考数学(文科)试题试卷 2012年高考数学三轮复习精编模拟套题(八)+参考答案
2012年高考数学三轮复习精编模拟套题(八)+参考答案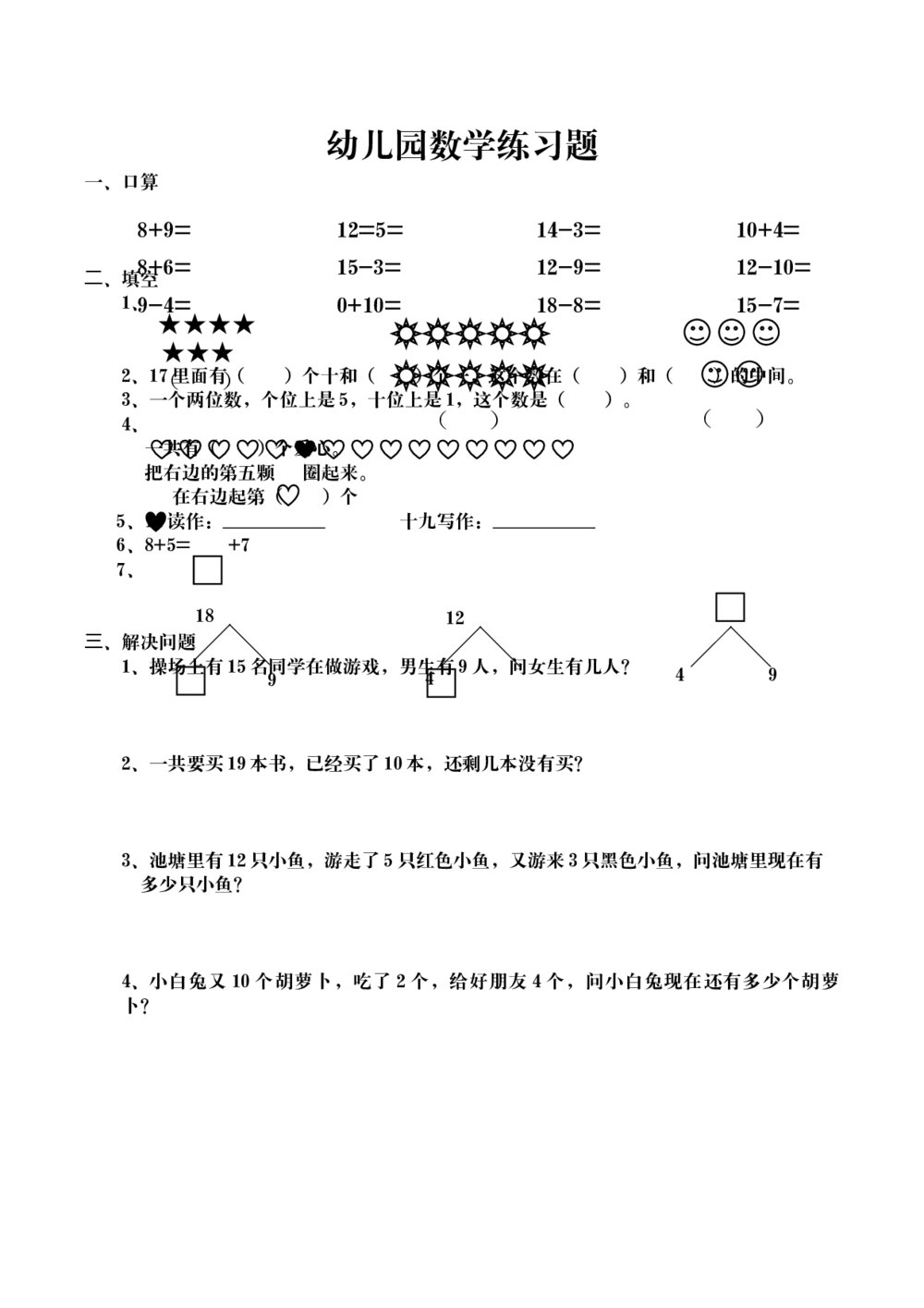 一年级幼儿园中大班数学练习题
一年级幼儿园中大班数学练习题