








《2017年高考数学知识方法专题4《三角函数与平面向量第17练 三角函数的化简与求值》》是由用户上传到老师板报网,本为文库资料,大小为764.5 KB,总共有9页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 9页
- 764.5 KB
- VIP模板
- doc
- 数字产品不支持退货
第17练 三角函数的化简与求值[题型分析·高考展望] 三角函数的化简与求值在高考中频繁出现,重点考查运算求解能力.运算包括对数字的计算、估值和近似计算,对式子的组合变形与分解变形,属于比较简单的题目,这就要求在解决此类题目时不能丢分,由于三角函数部分公式比较多,要熟练记忆、掌握并能灵活运用.体验高考1.(2015·课标全国Ⅰ)sin20°cos10°-cos160°sin10°等于( )A.-B.C.-D.答案 D解析 sin20°cos10°-cos160°sin10°=sin20°cos10°+cos20°sin10°=sin30°=.2.(2015·重庆)若tanα=2tan,则等于( )A.1B.2C.3D.4答案 C解析 ======3.3.(2016·课标全国甲)若cos=,则sin2α等于( )A.B.C.-D.-答案 D解析 因为sin2α=cos=2cos2-1,又因为cos=,所以sin2α=2×-1=-,故选D.4.(2016·课标全国丙)若tanα=,则cos2α+2sin2α等于( )A.B.C.1D.答案 A解析 tanα=,则cos2α+2sin2α===.5.(2016·四川)cos2-sin2=________.答案 解析 由题可知,cos2-sin2=cos=.高考必会题型题型一 利用同角三角函数基本关系式化简与求值基本公式:sin2α+cos2α=1;tanα=.基本方法:(1)弦切互化;(2)“1”的代换,即1=sin2α+cos2α;(3)在进行开方运算时,注意判断符号.例1 已知tanα=2,求:(1)的值;(2)3sin2α+3sinαcosα-2cos2α的值.解 (1)方法一 ∵tanα=2,∴cosα≠0,∴====.方法二 由tanα=2,得sinα=2cosα,代入得===.(2)3sin2α+3sinαcosα-2cos2α====.点评 本题(1)(2)两小题的共同点:都是正弦、余弦的齐次多项式.对于这样的多项式一定可以化成切函数,分式可以分子分母同除“cosα”的最高次幂,整式可以看成分母为“1”,然后用sin2α+cos2α代换“1”,变成分式后再化简.变式训练1 已知sin(3π+α)=2sin,求下列各式的值:(1);(2)sin2α+sin2α.解 由已知得sinα=2cosα.(1)原式==-.(2)原式===.题型二 利用诱导公式化简与求值1.六组诱导公式分两大类,一类是同名变换,即“函数名不变,符号看象限”;一类是异名变换,即“函数名称变,符号看象限”.2.诱导公式化简的基本原则:负化正,大化小,化到锐角为最好!例2 (1)设f(α)=,则f=______.(2)化简:+=________.答案 (1) (2)0解析 (1)∵f(α)====,∴f====.(2)原式=+=-sinα+sinα=0.点评 熟练运用诱导公式和基本关系式,并确定相应三角函数值的符号是解题的关键.另外,切化弦是常用的规律技巧.变式训练2 (1)(2016·课标全国乙)已知θ是第四象限角,且sin=,则tan=________.(2)已知cos=a(|a|≤1),则cos+sin=________.答案 (1)- (2)0解析 (1)将θ-转化为(θ+)-.由题意知sin(θ+)=,θ是第四象限角,所以cos(θ+)>0,所以cos(θ+)==.tan(θ-)=tan(θ+-)=-tan[-(θ+)]=-=-=-=-.(2)cos=cos=-cos=-a.sin=sin=cos=a,∴cos+sin=0.题型三 利用其他公式、代换等化简求值两角和与差的三角函数的规律有三个方面:(1)变角,目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”.(2)变名,通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”“升幂与降幂”等.(3)变式,根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有“常值代换”“逆用变用公式”“通分与约分”“分解与组合”“配方与平方”等.例3 化简:(1)sin50°(1+tan10°);(2).解 (1)sin50°(1+tan10°)=sin50°(1+tan60°tan10°)=sin50°·=sin50°·====1.(2)原式=====cos2x.点评 (1)二倍角公式是三角变换的主要公式,应熟记、巧用,会变形应用.(2)重视三角函数的“三变”:“三变”是指“变角、变名、变式”.变角:对角的分拆要尽可能化成同名、同角、特殊角;变名:尽可能减少函数名称;变式:对式子变形一般要尽可能有理化、整式化、降低次数等.在解决求值、化简、证明问题时,一般是观察角度、函数名、所求(或所证明)问题的整体形式中的差异,再选择适当的公式恒等变形.变式训练3 (1)在△ABC中,已知三个内角A,B,C成等差数列,则tan+tan+tantan的值为________.(2)的值是( )A.B.C.D.(3)若α∈,且3cos2α=sin,则sin2α的值为( )A.B.-C.D.-答案 (1) (2)C (3)D解析 (1)因为三个内角A,B,C成等差数列,且A+B+C=π,所以A+C=,=,tan=,所以tan+tan+tantan=tan+tantan=+tantan=.(2)原式====.(3)cos2α=sin=sin=2sincos代入原式,得6sincos=sin,∵α∈,sin(-α)≠0,∴cos=,∴sin2α=cos=2cos2-1=-.高考题型精练1.(2015·陕西)“sinα=cosα”是“cos2α=0”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案 A解析 ∵sinα=cosα⇒cos2α=cos2α-sin2α=0;cos2α=0⇔cosα=±sinα⇏sinα=cosα,故选A.2.(2016·课标全国丙)若tanθ=-,则cos2θ等于( )A.-B.-C.D.答案 D解析 tanθ=-,则cos2θ=cos2θ-sin2θ===.3.若tan=,且-<α<0,则等于( )A.-B.C.-D.答案 A解析 由tan==,得tanα=-.又-<α<0,所以sinα=-.故==2sinα=-.4.已知f(x)=sin2,若a=f(lg5),b=f(lg),则( )A.a+b=0B.a-b=0C.a+b=1D.a-b=1答案 C解析 a=f(lg5)=sin2(lg5+)==,b=f(lg)=sin2(lg+)==,则可得a+b=1.5.已知sin+sinα=,则sin的值是( )A.-B.C.D.-答案 D解析 sin+sinα=⇒sincosα+cossinα+sinα=⇒sinα+cosα=⇒sinα+cosα=,故sin=sinαcos+cosαsin=-=-.6.若(4tanα+1)(1-4tanβ)=17,则tan(α-β)等于( )A.B.C.4D.12答案 C解析 由已知得4tanα-16tanαtanβ+1-4tanβ=17,∴tanα-tanβ=4(1+tanαtanβ),∴tan(α-β)==4.7.(2015·江苏)已知tanα=-2,tan(α+β)=,则tanβ的值为________.答案 3解析 ∵tanα=-2,∴tan(α+β)===,解得tanβ=3.8.设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=________.答案 -解析 f(x)=sinx-2cosx==sin(x-φ),其中sinφ=,cosφ=,当x-φ=2kπ+(k∈Z)时,函数f(x)取到最大值,即θ=2kπ++φ时,函数f(x)取到最大值,所以cosθ=-sinφ=-.9.已知α∈,且2sin2α-sinα·cosα-3cos2α=0,则=_______.答案 解析 ∵α∈,且2sin2α-sinα·cosα-3cos2α=0,∴(2sinα-3cosα)(sinα+cosα)=0,∴2sinα=3cosα,又sin2α+cos2α=1,∴cosα=,sinα=,∴==.10.(2015·四川)已知sinα+2cosα=0,则2sinαcosα-cos2α的值是________.答案 -1解析 ∵sinα+2cosα=0,∴sinα=-2cosα,∴tanα=-2.又∵2sinαcosα-cos2α==,∴原式==-1.11.(2015·广东)已知tanα=2.(1)求tan的值;(2)求的值.解 (1)tan====-3.(2)=====1.12.已知函数f(x)=cos2x+sinxcosx,x∈R.(1)求f的值;(2)若sinα=,且α∈,求f.解 (1)f=cos2+sincos=2+×=.(2)因为f(x)=cos2x+sinxcosx=+sin2x=+(sin2x+cos2x)=+sin,所以f=+sin=+sin=+.又因为sinα=,且α∈,所以cosα=-,所以f=+=.展开内容









 20以内数字加减法练习(word版)
20以内数字加减法练习(word版)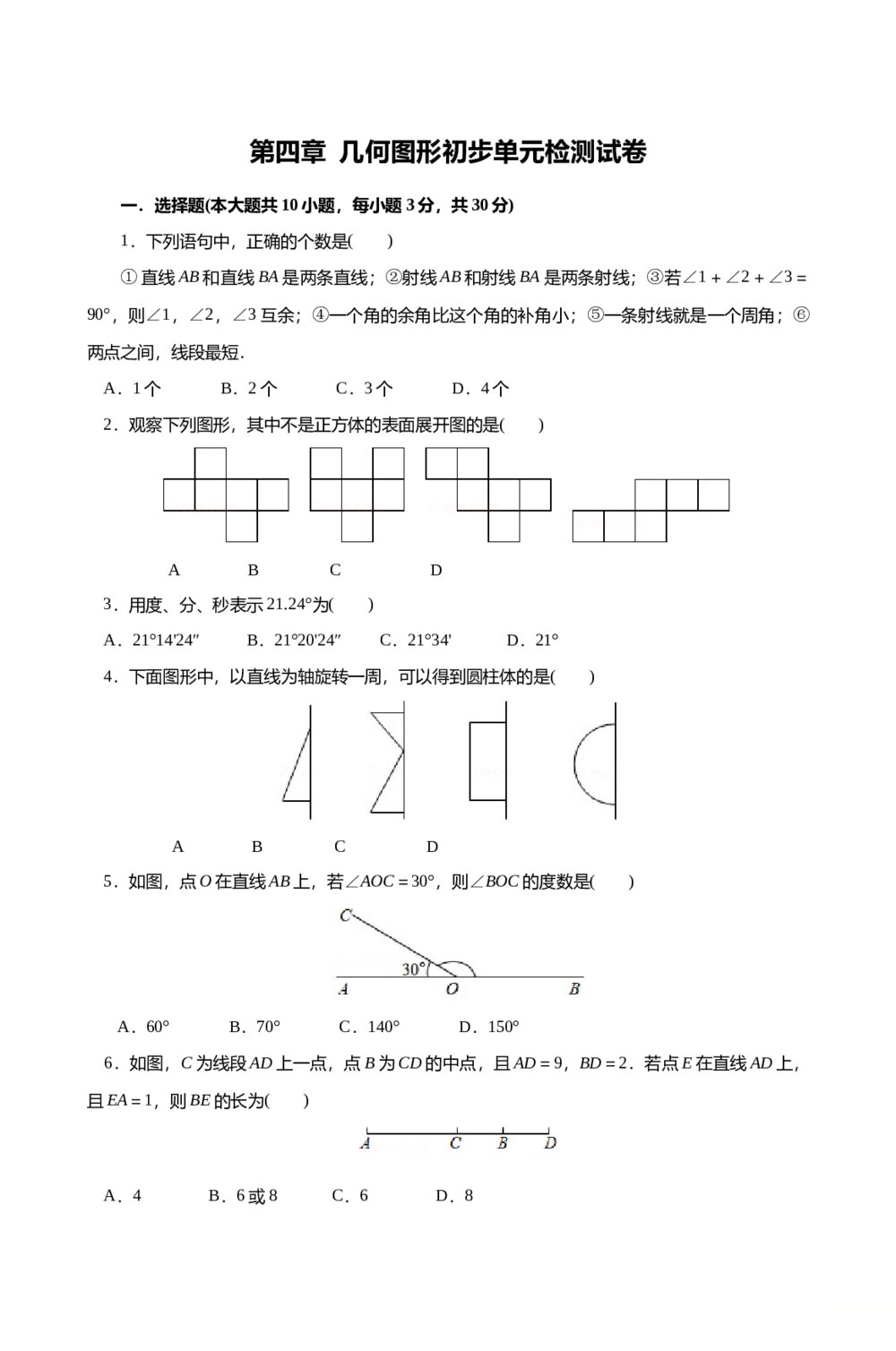 人教版七年级数学上册《第四章·几何图形初步单元检测试卷》+(含参考答案)
人教版七年级数学上册《第四章·几何图形初步单元检测试卷》+(含参考答案) 北京市石景山区高三一模数学文科+参考答案
北京市石景山区高三一模数学文科+参考答案 2011年全国统一高考数学试卷(理科)(大纲版)+(答案解析)
2011年全国统一高考数学试卷(理科)(大纲版)+(答案解析) 重庆卷2011全国高考(理科)数学试卷
重庆卷2011全国高考(理科)数学试卷 小学二年级数学应用题专项训练word
小学二年级数学应用题专项训练word