









试读已结束,还剩1页未读,您可下载完整版后进行离线阅读
《2009年北京高考(文科)数学试卷+答案解析》是由用户上传到老师板报网,本为文库资料,大小为393.5 KB,总共有11页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 11页
- 393.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2009年普通高等学校招生全国统一考试数学(文史类)(北京卷)本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟。考试结束后,将本试卷和答题卡一并交回。第I卷(选择题共40分)注意事项:1.答第I卷前,考生务必将答题卡上的姓名、准考证号用黑色字迹的签字笔填写,用2B铅笔将准考证号对应的信息点涂黑。2.每小题选出答案后,将答题卡上对应题目的答案选中涂满涂黑,黑度以盖住框内字母为准,修改时用橡皮擦除干净。在试卷上作答无效。一、本大题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。1.设集合21{|2},{1}2AxxBxx,则AB()A.{12}xxB.1{|1}2xxC.{|2}xxD.{|12}xx【答案】A【解析】本题主要考查集合的基本运算以及简单的不等式的解法.属于基础知识、基本运算的考查.∵1{|2},2Axx2{1}|11Bxxxx,∴{12}ABxx,故选A.2.已知向量(1,0),(0,1),(),abckabkRdab,如果//cd,那么A.1k且c与d同向B.1k且c与d反向C.1k且c与d同向D.1k且c与d反向【答案】D.w【解析】.k.s.5.u.c本题主要考查向量的共线(平行)、向量的加减法.属于基础知识、基本运算的考查.∵a1,0,b0,1,若1k,则cab1,1,dab1,1,显然,a与b不平行,排除A、B.若1k,则cab1,1,dab1,1,即c//d且c与d反向,排除C,故选D3.若4(12)2(,abab为有理数),则ab()A.33B.29C.23D.19【答案】B.w【解析】本题主要考查二项式定理及其展开式.属于基础知识、基本运算的考查.∵40123401234444441222222CCCCC1421282417122,由已知,得171222ab,∴171229ab.故选B..k.s.5.u.c4.为了得到函数3lg10xy的图像,只需把函数lgyx的图像上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度【答案】C.w【解析】本题主要考查函数图象的平移变换.属于基础知识、基本运算的考查.A.lg31lg103yxx,B.lg31lg103yxx,C.3lg31lg10xyx,D.3lg31lg10xyx.故应选C.5.用数字1,2,3,4,5组成的无重复数字的四位偶数的个数为()A.8B.24C.48D.120【答案】C.w【解析】本题主要考查排列组合知识以及分步计数原理知识.属于基础知识、基本运算的考查.2和4排在末位时,共有122A种排法,其余三位数从余下的四个数中任取三个有3443224A种排法,于是由分步计数原理,符合题意的偶数共有22448(个).故选C.6.“6”是“1cos22”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A.w【解析】本题主要考查.k本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断.属于基础知识、基本运算的考查.当6时,1cos2cos32,反之,当1cos22时,有2236kkkZ,或2236kkkZ,故应选A.7.若正四棱柱1111ABCDABCD的底面边长为1,1AB与底面ABCD成60°角,则11AC到底面ABCD的距离为()A.33B.1C.2D.3【答案】D.w【解析】.k本题主要考查正四棱柱的概念、直线与平面所成的角以及直线与平面的距离等概念.属于基础知识、基本运算的考查.依题意,160BAB,如图,11tan603BB,故选D.8.设D是正123PPP及其内部的点构成的集合,点0P是123PPP的中心,若集合0{|,||||,1,2,3}iSPPDPPPPi,则集合S表示的平面区域是()A.三角形区域B.四边形区域C.五边形区域D.六边形区域【答案】D【解析】本题主要考查集合与平面几何基础知识..5.u.c.o.本题主要考查阅读与理解、信息迁移以及学生的学习潜力,考查学生分析问题和解决问题的能力.属于创新题型.大光明如图,A、B、C、D、E、F为各边三等分点,答案是集合S为六边形ABCDEF,其中,021,3iPAPAPAi即点P可以是点A.第Ⅱ卷(110分)注意事项:1.用铅笔或圆珠笔将答案直接写在试卷上。2.答卷前将密封线内的项目填写清楚。题号二三总分151617181920分数二、填空题:本大题共6小题,每小题5分,共30分。把答案填写在题中横线上。9.若4sin,tan05,则cos.【答案】35【解析】本题主要考查简单的三角函数的运算。属于基础知识、基本运算的考查。由已知,在第三象限,∴2243cos1sin155,∴应填35.10.若数列{}na满足:111,2()nnaaanN,则5a;前8项的和8S.(用数字作答)【答案】16255.w【解析】本题主要考查简单的递推数列以及数列的求和问题.m属于基础知识、基本运算的考查.1213243541,22,24,28,216aaaaaaaaa,易知882125521S,∴应填255.11.若实数,xy满足20,4,5,xyxx则sxy的最大值为.【答案】9【解析】.s.5.u本题主要考查线性规划方面的基础知.属于基础知识、基本运算的考查.如图,当4,5xy时,459sxy为最大值.故应填9.12.已知函数3,1,(),1,xxfxxx若()2fx,则x..w.w.k.s.5【答案】3log2.w【解析】5.u.c本题主要考查分段函数和简单的已知函数值求x的值.属于基础知识、基本运算的考查.由31log232xxx,122xxx无解,故应填3log2.13.椭圆22192xy的焦点为12,FF,点P在椭圆上,若1||4PF,则2||PF;12FPF的大小为.【答案】2,120.w【解析】u.c本题主要考查椭圆的定义、焦点、长轴、短轴、焦距之间的关系以及余弦定理.属于基础知识、基本运算的考查.∵229,3ab,∴22927cab,∴1227FF,又1124,26PFPFPFa,∴22PF,又由余弦定理,得2221224271cos2242FPF,∴12120FPF,故应填2,120.14.设A是整数集的一个非空子集,对于kA,如果1kA且1kA,那么称k是A的一个“孤立元”,给定{1,2,3,4,5,6,7,8,}S,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有个.【答案】6【解析】本题主要考查阅读与理解、信息迁移以及学生的学习潜力,考查学生分析问题和解决问题的能力.属于创新题型.什么是“孤立元”?依题意可知,必须是没有与k相邻的元素,因而无“孤立元”是指在集合中有与k相邻的元素.故所求的集合可分为如下两类:因此,符合题意的集合是:1,2,3,2,3,4,3,4,5,4,5,6,5,6,7,6,7,8共6个.故应填6.三、解答题:本大题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。15.(本小题共12分)已知函数()2sin()cosfxxx.(Ⅰ)求()fx的最小正周期;(Ⅱ)求()fx在区间,62上的最大值和最小值.【解析】本题主要考查特殊角三角函数值、诱导公式、二倍角的正弦、三角函数在闭区间上的最值等基础知识,主要考查基本运算能力.(Ⅰ)∵2sincos2sincossin2fxxxxxx,∴函数()fx的最小正周期为.(Ⅱ)由2623xx,∴3sin212x,∴()fx在区间,62上的最大值为1,最小值为32.16.(本小题共14分)如图,四棱锥PABCD的底面是正方形,PDABCD底面,点E在棱PB上.(Ⅰ)求证:平面AECPDB平面;(Ⅱ)当2PDAB且E为PB的中点时,求AE与平面PDB所成的角的大小.【解法1】本题主要考查直线和平面垂直、平面与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力和推理论证能力.(Ⅰ)∵四边形ABCD是正方形,∴ACBD⊥,∵PDABCD底面,∴PDAC⊥,∴AC⊥平面PDB,∴平面AECPDB平面.(Ⅱ)设AC∩BD=O,连接OE,由(Ⅰ)知AC⊥平面PDB于O,∴AEO∠为AE与平面PDB所的角,∴O,E分别为DB、PB的中点,OE//PD∴,12OEPD,又∵PDABCD底面,∴OE⊥底面ABCD,OE⊥AO,在Rt△AOE中,1222OEPDABAO,∴45AEO,即AE与平面PDB所成的角的大小为45.【解法2】如图,以D为原点建立空间直角坐标系Dxyz,设,,ABaPDh则,0,0,,,0,0,,0,0,0,0,0,0,AaBaaCaDPh,(Ⅰ)∵,,0,0,0,,,,0ACaaDPhDBaa,∴0,0ACDPACDB,∴ACDP⊥,AC⊥BD,∴AC⊥平面PDB,∴平面AECPDB平面.(Ⅱ)当2PDAB且E为PB的中点时,1120,0,2,,,222PaEaaa,设ACBDO,则11(,,0)22Oaa,连接OE,由(Ⅰ)知AC⊥平面PDB于O,∴AEO∠为AE与平面PDB所成的角,∵1122,,,0,0,2222EAaaaEOa,∴2cos2EAEOAEOEAEO,∴45AEO,即AE与平面PDB所成的角的大小为45.17.(本小题共13分)某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,遇到红灯时停留的时间都是2min.(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率【解析】本题主要考查随机事件、互斥事件、相互独立事件等概率的基础知识,考查运用概率知识解决实际问题的能力.(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为11141133327PA.(Ⅱ)设这名学生在上学路上因遇到红灯停留的总时间至多是4min为事件B,这名学生在上学路上遇到k次红灯的事件0,1,2kBk.则由题意,得40216381PB,132212142412321224,33813381PBCPBC.由于事件B等价于“这名学生在上学路上至多遇到两次红灯”,∴事件B的概率为01289PBPBPBPB.18.(本小题共14分)设函数3()3(0)fxxaxba.(Ⅰ)若曲线()yfx在点(2,(2))f处与直线8y相切,求,ab的值;(Ⅱ)求函数()fx的单调区间与极值点.【解析】本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力.(Ⅰ)\'233fxxa,∵曲线()yfx在点(2,(2))f处与直线8y相切,∴\'203404,24.86828faababf(Ⅱ)∵\'230fxxaa,当0a时,\'0fx,函数()fx在,上单调递增,此时函数()fx没有极值点.当0a时,由\'0fxxa,当,xa时,\'0fx,函数()fx单调递增,当,xaa时,\'0fx,函数()fx单调递减,当,xa时,\'0fx,函数()fx单调递增,∴此时xa是()fx的极大值点,xa是()fx的极小值点.19.(本小题共14分)已知双曲线2222:1(0,0)xyCabab的离心率为3,右准线方程为33x。(Ⅰ)求双曲线C的方程;(Ⅱ)已知直线0xym与双曲线C交于不同的两点A,B,且线段AB的中点在圆225xy上,求m的值【解析】本题主要考查双曲线的标准方程、圆的切线方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法,考查推理、运算能力.(Ⅰ)由题意,得2333acca,解得1,3ac,∴2222bca,∴所求双曲线C的方程为2212yx.(Ⅱ)设A、B两点的坐标分别为1122,,,xyxy,线段AB的中点为00,Mxy,由22012xymyx得22220xmxm(判别式0),∴12000,22xxxmyxmm,∵点00,Mxy在圆225xy上,∴2225mm,∴1m.20.(本小题共13分)设数列{}na的通项公式为(,0)napnqnNP.数列{}nb定义如下:对于正整数m,mb是使得不等式nam成立的所有n中的最小值.(Ⅰ)若11,23pq,求3b;(Ⅱ)若2,1pq,求数列{}mb的前2m项和公式;(Ⅲ)是否存在p和q,使得32()mbmmN?如果存在,求p和q的取值范围;如果不存在,请说明理由.【解析】本题主要考查数列的概念、数列的基本性质,考查运算能力、推理论证能力、分类讨论等数学思想方法.本题是数列与不等式综合的较难层次题.(Ⅰ)由题意,得1123nan,解11323n,得203n.∴11323n成立的所有n中的最小正整数为7,即37b.(Ⅱ)由题意,得21nan,对于正整数m,由nam,得12mn.根据mb的定义可知当21mk时,*mbkkN;当2mk时,*1mbkkN.∴1221321242mmmbbbbbbbbb1232341mm213222mmmmmm.(Ⅲ)假设存在p和q满足条件,由不等式pnqm及0p得mqnp.∵32()mbmmN,根据mb的定义可知,对于任意的正整数m都有3132mqmmp,即231pqpmpq对任意的正整数m都成立.当310p(或310p)时,得31pqmp(或231pqmp),这与上述结论矛盾!当310p,即13p时,得21033qq,解得2133q.(经检验符合题意)∴存在p和q,使得32()mbmmN;p和q的取值范围分别是13p,2133q.展开内容










![六年级数学奥数《第五讲[1]几何-立体部分》教师版PPT课件](https://img.banbaow.com/uploadfile/2023/0601/80d687a3965e58674594f/0.jpg) 六年级数学奥数《第五讲[1]几何-立体部分》教师版PPT课件
六年级数学奥数《第五讲[1]几何-立体部分》教师版PPT课件 2011海淀区高三二模数学期末练习试卷(理科)+答案
2011海淀区高三二模数学期末练习试卷(理科)+答案 2019年上海高考数学真题试卷+(答案解析word版)
2019年上海高考数学真题试卷+(答案解析word版)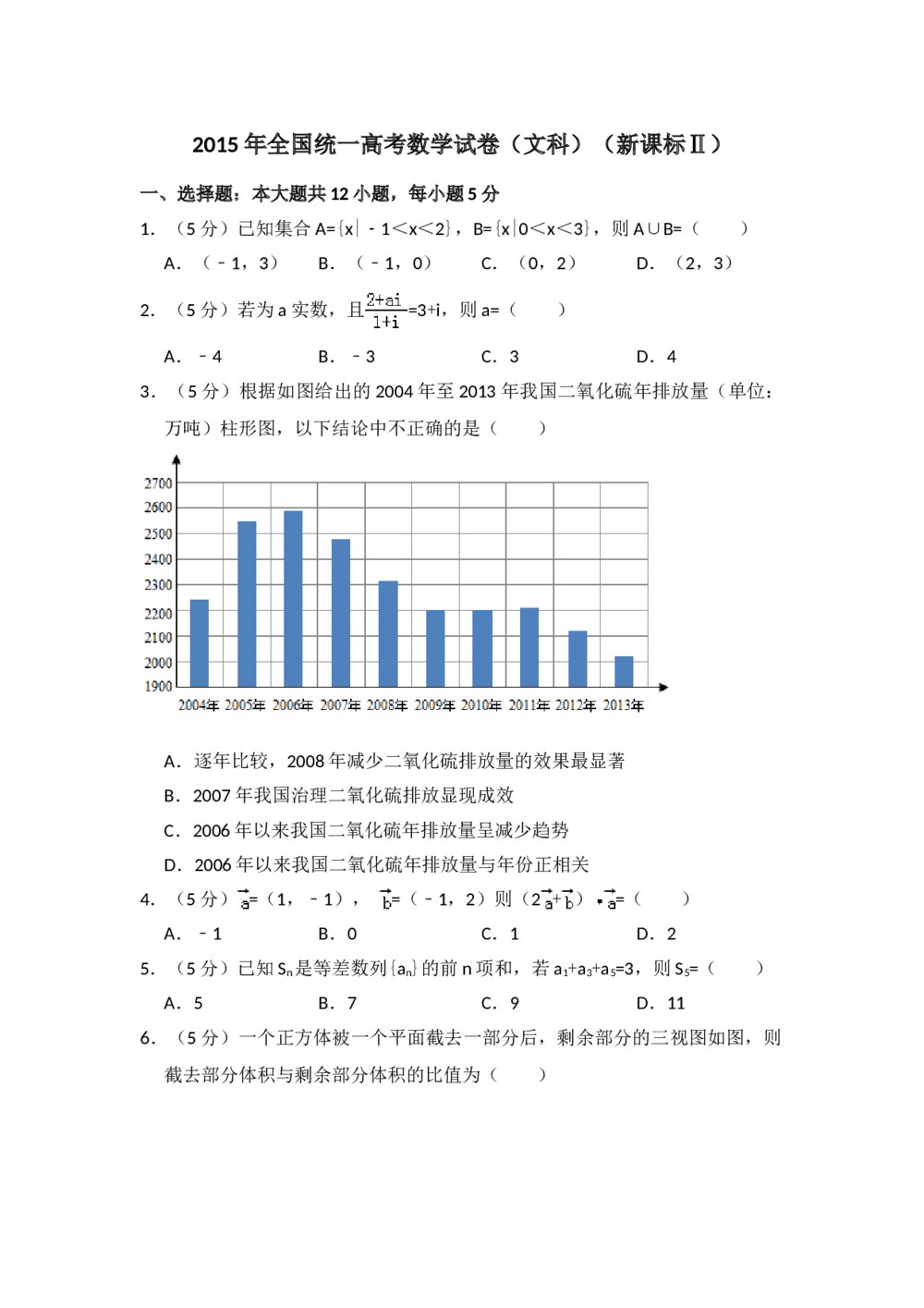 2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析
2015年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析 人教版小学数学六年级上期末阶段检测(4)+参考答案
人教版小学数学六年级上期末阶段检测(4)+参考答案 人教版数学二年级下册《归类达标测试卷3·几何与统计推理》试题word版+(答案)
人教版数学二年级下册《归类达标测试卷3·几何与统计推理》试题word版+(答案)