









试读已结束,还剩9页未读,您可下载完整版后进行离线阅读
《2020年上海高考数学试卷试题+参考答案》是由用户上传到老师板报网,本为文库资料,大小为549.71 KB,总共有19页,格式为docx。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 19页
- 549.71 KB
- VIP模板
- docx
- 数字产品不支持退货
2020年全国高考数学真题试卷及解析(上海卷)一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)1.已知集合,2,,集合,4,,则 .2.计算: .3.已知复数为虚数单位),则 .4.已知函数,是的反函数,则 .5.已知、满足,则的最大值为 .6.已知行列式,则 .7.已知有四个数1,2,,,这四个数的中位数是3,平均数是4,则 .8.已知数列是公差不为零的等差数列,且,则 .9.从6个人挑选4个人去值班,每人值班一天,第一天安排1个人,第二天安排1个人,第三天安排2个人,则共有 种安排情况.10.已知椭圆的右焦点为,直线经过椭圆右焦点,交椭圆于、4}{2B5}AB1lim31nnn12(zii||z3()fxx()fx()fx()fxxy202300xyxyy…„…2zyx126300abcdabcdabab{}na1109aaa12910aaaa22:143xyCFlFCPQ两点(点在第二象限),若点关于轴对称点为,且满足,求直线的方程是 .11.设,若存在定义域为的函数同时满足下列两个条件:(1)对任意的,的值为或;(2)关于的方程无实数解,则的取值范围是 .12.已知,,,,,是平面内两两互不相等的向量,满足,且,(其中,2,,2,,,则的最大值是.二、选择题(本大题共4题,每题5分,共20分)13.下列等式恒成立的是 A.B.C.D.14.已知直线方程的一个参数方程可以是 A.为参数)B.为参数)C.为参数)D.为参数)PQxQPQFQlaRR()fx0xR0()fx0x20xx()fxaa1a2a1b2b(*)kbkN12||1aa||{1ijab2}1i1j)kk()222abab„222abab…2||abab…222abab„3410xy()13(14xttyt14(13xttyt13(14xttyt14(13xttyt15.在棱长为10的正方体中,为左侧面上一点,已知点到的距离为3,到的距离为2,则过点且与平行的直线相交的面是 A.B.C.D.16.命题:存在且,对于任意的,使得(a);命题单调递减且恒成立;命题单调递增,存在使得,则下列说法正确的是 A.只有是的充分条件B.只有是的充分条件C.,都是的充分条件D.,都不是的充分条件三、解答题(本大题共5题,共14+14+14+16+18=76分)17.(14分)已知是边长为1的正方形,正方形绕旋转形成一个圆柱.(1)求该圆柱的表面积;1111ABCDABCDP11ADDAP11ADP1AAP1AC()11AABB11BBCC11CCDDABCDpaR0axR()()fxafxf1:()qfx()0fx2:()qfx00x0()0fx()1qp2qp1q2qp1q2qpABCDABCDAB(2)正方形绕逆时针旋转至,求线段与平面所成的角.18.(14分)已知函数,.(1)的周期是,求,并求的解集;(2)已知,,,,求的值域.19.(14分)在研究某市场交通情况时,道路密度是指该路段上一定时间内通过的车辆数除以时间,车辆密度是该路段一定时间内通过的车辆数除以该路段的长度,现定义交通流量为,为道路密度,为车辆密度..ABCDAB211ABCD1CDABCD()sinfxx0()fx41()2fx12()()3()()2gxfxfxfx[0x]4()gxqvxxq1100135(),040()3(40)85,4080xxvfxkxx„„(1)若交通流量,求道路密度的取值范围;(2)已知道路密度,交通流量,求车辆密度的最大值.20.(16分)已知双曲线与圆交于点,(第一象限),曲线为、上取满足的部分.(1)若,求的值;(2)当,与轴交点记作点、,是曲线上一点,且在第一象限,且,求;(3)过点斜率为的直线与曲线只有两个交点,记为、,用表示,并求的取值范围.95vx80x50vq2212:14xyb2222:4(0)xybb(AAx)Ay12||Axx6Axb5b2x1F2FP1||8PF12FPF2(0,2)2bD2blMNbOMONOMON21.(18分)已知数列为有限数列,满足,则称满足性质.(1)判断数列3、2、5、1和4、3、2、5、1是否具有性质,请说明理由;(2)若,公比为的等比数列,项数为10,具有性质,求的取值范围;(3)若是1,2,3,,的一个排列,符合,2,,,、都具有性质,求所有满足条件的数列.{}na12131||||||maaaaaa„„„{}naPP11aqPq{}nam(4)m…{}nb1(1kkbak1)m{}na{}nbP{}na参考答案1.,【解析】因为,2,,,4,,则,.故答案为:,.2.【解析】,故答案为:.3.【解析】由,得.故答案为:.4.【解析】由,得,把与互换,可得的反函数为.故答案为:.5.-1{1A3}{2B5}{2AB4}1111lim1101limlim113130333limnnnnnnnnnn12zi22||1(2)5z3()yfxx3xyxy3()fxx13()fxx【解析】由约束条件作出可行域如图阴影部分,化目标函数为,由图可知,当直线过时,直线在轴上的截距最大,联立,解得,即.有最大值为.故答案为:.6.2【解析】行列式,可得,解得.故答案为:2.7.36【解析】因为四个数的平均数为4,所以,因为中位数是3,所以,解得,代入上式得,所以,故答案为:36.202300xyxyy…„…2zyx2yxz2yxzAy20230xyxy11xy(1,1)Az12111126300abcd36abcd2abcd441213ab232a4a1349b36ab8.【解析】根据题意,等差数列满足,即,变形可得,所以.故答案为:.9.180【解析】根据题意,可得排法共有种.故答案为:180.10.【解析】椭圆的右焦点为,直线经过椭圆右焦点,交椭圆于、两点(点在第二象限),若点关于轴对称点为,且满足,可知直线的斜率为,所以直线的方程是:,即.故答案为:.{}na1109aaa11198aadad1ad1129110119899369362729998daaaaadddaadaddd112654180CCC22:143xyC(1,0)FlFCPQPQxQPQFQl1l(1)yx10xy11.,,,【解析】根据条件(1)可得或(1),又因为关于的方程无实数解,所以或1,故,,,,故答案为:,,,.12.6【解析】如图,设,,由,且,,分别以,为圆心,以1和2为半径画圆,其中任意两圆的公共点共有6个.故满足条件的的最大值为6.故答案为:6.13.B(0)0ff1x()fxa0a(a0)(01)(1)11OAa22OAa12||1aa||{1ijab2}1A2Ak【解析】.显然当,时,不等式不成立,故错误;.,,,故正确;.显然当,时,不等式不成立,故错误;.显然当,时,不等式不成立,故错误.故选:.14.B【解析】为参数)的普通方程为:,即,不正确;为参数)的普通方程为:,即,正确;为参数)的普通方程为:,即,不正确;为参数)的普通方程为:,即,不正确;故选:.15.D【解析】如图,A0a0b222abab„AB2()0ab…2220abab…222abab…BC0a0b2||abab…CD0a0b222abab„DB13(14xttyt1314xy4310xy14(13xttyt1413xy3410xy13(14xttyt1314xy4310xy14(13xttyt1413xy3470xyB由点到的距离为3,到的距离为2,可得在△内,过作,且于,于,在平面中,过作,交于,则平面平面.连接,交于,连接,平面平面,平面平面,平面平面,.在中,过作,且于,则.线段在四边形内,在线段上,在四边形内.过点且与平行的直线相交的面是.故选:.16.C【解析】对于命题:当单调递减且恒成立时,当时,此时,又因为单调递减,所以P11ADP1AAP1AADP1//EFAD1EFAAEEFADFABCDF//FGCDBCG//EFG1ADCACFGMEM//EFG1ADC1AAC11ADCAC1AACEFMEM1//EMACEFMP//PNEMPNFMN1//PNACFMABCDNFMNABCDP1ACABCDD1q()fx()0fx0axax()fx()()fxafx又因为恒成立时,所以(a),所以(a),所以命题命题,对于命题:当单调递增,存在使得,当时,此时,(a),又因为单调递增,所以,所以(a),所以命题命题,所以,都是的充分条件,故选:.17.【解析】(1)该圆柱的表面由上下两个半径为1的圆面和一个长为、宽为1的矩形组成,.故该圆柱的表面积为.(2)正方形,,又,,,且、平面,平面,即在面上的投影为,连接,则即为线段与平面所成的角,而,线段与平面所成的角为.18.【解析】(1)由于的周期是,所以,所以.()0fx()()fxfxf()()fxafxf1qp2q()fx00x0()0fx00axxaxf0()0fx()fx()()fxafx()()fxafxf2pp1q2qpC2221214S411ABCD1ADAB12DAD1ADADADABAADABADB1ADADB1DADBA1CD1DCA1CDABCD1126cos33ACDCACD1CDABCD()fx421421()sin2fxx令,故或,整理得或.故解集为或,.(2)由于,所以.所以由于,,所以.,故,故.所以函数的值域为.19.【解析】(1),越大,越小,是单调递减函数,,当时,最大为85,于是只需令,解得,故道路密度的取值范围为.(2)把,代入中,得,解得.11sin22x1226xk526k43xk543xk{|43xxk543xk}kZ1()sinfxx21cos233111()sin3sin()sin()sin2sin2cos2sin(2)22222226xgxxxxxxxx[0x]422663x„„1sin(2)126x„„11sin(2)62x„„1()02gx„„()gx1[,0]2qvxvx()vfx0k4080x„„v1100135()953x3xx(3,40)80x50v()(40)85vfxkx504085k78k,当时,单调递增,;当时,是关于的二次函数,开口向下,对称轴为,此时有最大值,为.故车辆密度的最大值为.20.【解析】(1)由,点为曲线与曲线的交点,联立,解得,;(2)由题意可得,为曲线的两个焦点,由双曲线的定义可得,又,,所以,因为,则,所以,在△中,由余弦定理可得,由,可得;1100135(),04037(40)85,40808xxxxqvxxxxx„„040xq40110040135()4040003q4080x„„qx4807xq2748048028800()12040008777q2880076AxA12222222144AAAAxybxyb2Ay2b1F2F112||||2PFPFa1||8PF24a2||844PF5b453c12||6FF12PFF22212121212||||||cos2||||PFPFFFFPFPFPF6416361128416120FPF1211arccos16FPF(3)设直线,可得原点到直线的距离,所以直线是圆的切线,设切点为,所以,并设与圆联立,可得,可得,,即,注意直线与双曲线的斜率为负的渐近线平行,所以只有当时,直线才能与曲线有两个交点,由,可得,所以有,解得或(舍去),因为为在上的投影可得,,所以,则,.21.【解析】(1)对于数列3,2,5,1,有,,,满足题意,该数列满足性质;对于第二个数列4、3、2、5、1,,,.不满足题意,该数列不满足性质.(2)由题意:,可得:,,3,,,24:22bblyxOl2224||2414bdbblM2OMkb2:OMyxb2224xyb222244xxbbxb2y(,2)Mbl2Ayl222222144AAAAxybxyb422Abyab4244bb2225b2225bOMONOM24OMONb24625OMONb(625OMON)|23|1|53|2|13|2P|34|1|24|2|54|1P11111||||nnaaqaaq…1|1||1|nnqq…{2n9}两边平方可得:,整理可得:,当时,得此时关于恒成立,所以等价于时,,所以,,所以,或,所以取,当时,得,此时关于恒成立,所以等价于时,,所以,所以,所以取.当时:,当为奇数时,得,恒成立,当为偶数时,,不恒成立;故当时,矛盾,舍去.当时,得,当为奇数时,得,恒成立,当为偶数时,,恒成立;故等价于时,,所以,所以或,所以取,综上,.22212121nnnnqqqq…11(1)[(1)2]0nnqqqq…1q…1(1)20nqq…n2n(1)20qq…(2)(1)0qq…2q„1q…1q…01q„1(1)20nqq„n2n(1)20qq„(2)(1)0qq„21q„„01q„10q„11[(1)2]0nnqqq„n1(1)20nqq„n1(1)20nqq…10q„1q11[(1)2]0nnqqq„n1(1)20nqq„n1(1)20nqq…2n(1)20qq…(2)(1)0qq…2q„1q…2q„(q2](0,)(3)设,,4,,,,因为,可以取,或,可以取,或,如果或取了或,将使不满足性质;所以的前5项有以下组合:①,;;;;②,;;;;③,;;;;④,;;;;对于①,,,,与满足性质矛盾,舍去;对于②,,,,与满足性质矛盾,舍去;对于③,,,,与满足性质矛盾,舍去;对于④,,,与满足性质矛盾,舍去;所以,4,,,,均不能同时使、都具有性质.当时,有数列,2,3,,,满足题意.当时,有数列,,,3,2,1满足题意.1ap{3p3m2}m1ap2a1p1p3a2p2p2a3a3p3p{}naP{}na1ap21ap31ap42ap52ap1ap21ap31ap42ap52ap1ap21ap31ap42ap52ap1ap21ap31ap42ap52ap11bp21||2bb31||1bb{}nbP11bp21||2bb31||3bb41||2bb{}nbP11bp21||2bb31||3bb41||1bb{}nbP11bp21||2bb31||1bb{}nbP{3P3m2}m{}na{}nbP1p{}:1na1mmpm{}:namm当时,有数列,1,3,,,满足题意.当时,有数列,,,,,3,2,1满足题意.所以满足题意的数列只有以上四种。2p{}:2na1mm1pm{}:1namm2m3m{}na










 2020年高考真题数学试卷(理科)(新课标Ⅱ)(原卷版))+(答案解析)
2020年高考真题数学试卷(理科)(新课标Ⅱ)(原卷版))+(答案解析) 2011年高考一轮课时训练(理)2.3数学归纳法+答案解析(通用版).DOC
2011年高考一轮课时训练(理)2.3数学归纳法+答案解析(通用版).DOC 2016年高考文科数学(新课标Ⅰ)+(参考答案)
2016年高考文科数学(新课标Ⅰ)+(参考答案)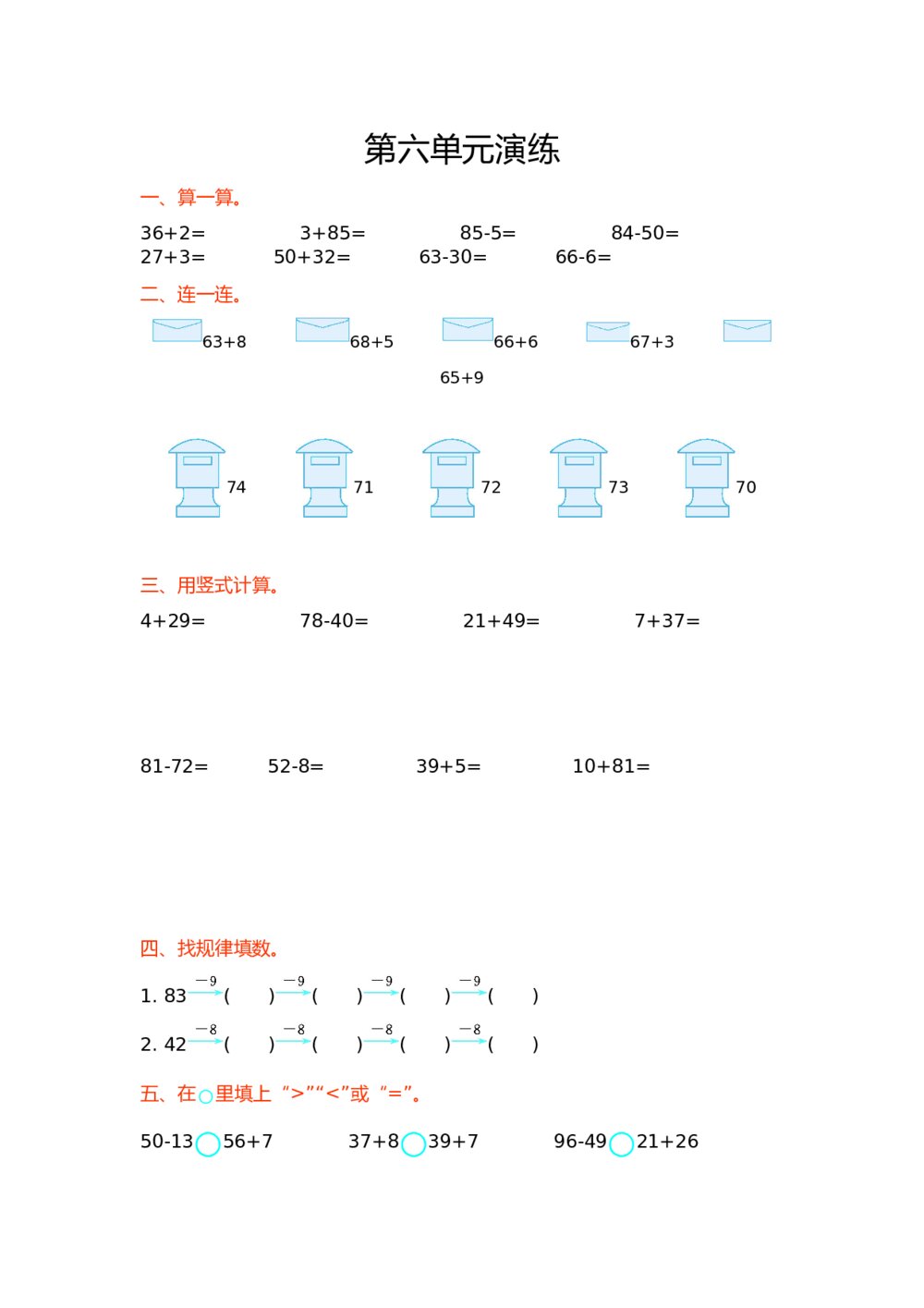 新北师大版小学一年级下册数学第六单元精品试卷有答案
新北师大版小学一年级下册数学第六单元精品试卷有答案 2021年全国新高考试卷数学试题+(答案解析版pdf)
2021年全国新高考试卷数学试题+(答案解析版pdf) 人教版一年级数学下册期末总复习试题全集word
人教版一年级数学下册期末总复习试题全集word