









试读已结束,还剩25页未读,您可下载完整版后进行离线阅读
《最新6年高考4年模拟试题试卷--第一章第一节集合(答案解析)》是由用户上传到老师板报网,本为文库资料,大小为1.95 MB,总共有35页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 35页
- 1.95 MB
- VIP模板
- doc
- 数字产品不支持退货
第一章集合与常用逻辑用语第一节集合第一部分六年高考荟萃2010年高考题一、选择题1.(2010浙江理)(1)设P={x︱x<4},Q={x︱2x<4},则(A)pQ(B)QP(C)RpQC(D)RQPC答案B【解析】22<<xxQ,可知B正确,本题主要考察了集合的基本运算,属容易题2.(2010陕西文)1.集合A={x-1≤x≤2},B={xx<1},则A∩B=()(A){xx<1}(B){x-1≤x≤2}(C){x-1≤x≤1}(D){x-1≤x<1}答案D【解析】本题考查集合的基本运算由交集定义得{x-1≤x≤2}∩{xx<1}={x-1≤x<1}3.(2010辽宁文)(1)已知集合1,3,5,7,9U,1,5,7A,则UCA(A)1,3(B)3,7,9(C)3,5,9(D)3,9答案D【解析】选D.在集合U中,去掉1,5,7,剩下的元素构成.UCA4.(2010辽宁理)1.已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},uðB∩A={9},则A=(A){1,3}(B){3,7,9}(C){3,5,9}(D){3,9}答案D【命题立意】本题考查了集合之间的关系、集合的交集、补集的运算,考查了同学们借助于Venn图解决集合问题的能力。【解析】因为A∩B={3},所以3∈A,又因为uðB∩A={9},所以9∈A,所以选D。本题也可以用Venn图的方法帮助理解。5.(2010全国卷2文)(A)1,4(B)1,5(C)2,4(D)2,5答案C解析:本题考查了集合的基本运算.属于基础知识、基本运算的考查.∵A={1,3}。B={3,5},∴{1,3,5}AB,∴(){2,4}UCAB故选C.6.(2010江西理)2.若集合A=|1xxxR,,2B=|yyxxR,,则AB=()A.|11xxB.|0xxC.|01xxD.答案C【解析】考查集合的性质与交集以及绝对值不等式运算。常见的解法为计算出集合A、B;{|11}Axx,{|0}Byy,解得AB={x|01}x。在应试中可采用特值检验完成。7.(2010安徽文)(1)若A=|10xx,B=|30xx,则AB=(A)(-1,+∞)(B)(-∞,3)(C)(-1,3)(D)(1,3)答案C【解析】(1,),(,3)AB,(1,3)AB,故选C.【方法总结】先求集合A、B,然后求交集,可以直接得结论,也可以借助数轴得交集.8.(2010浙江文)(1)设2{|1},{|4},PxxQxx则PQ(A){|12}xx(B){|31}xx(C){|14}xx(D){|21}xx答案D解析:22<<xxQ,故答案选D,本题主要考察了集合的基本运算,属容易题9.(2010山东文)(1)已知全集UR,集合240Mxx,则UCM=A.22xxB.22xxC.22xxx或D.22xxx或答案:C10.(2010北京文)⑴集合2{03},{9}PxZxMxZx,则PMI=(A){1,2}(B){0,1,2}(C){1,2,3}(D){0,1,2,3}答案:B11.(2010北京理)(1)集合2{03},{9}PxZxMxZx,则PMI=(A){1,2}(B){0,1,2}(C){x|0≤x<3}(D){x|0≤x≤3}答案:B12.(2010天津文)(7)设集合Ax||x-a|<1,xR,|15,.ABBxxxR若,则实数a的取值范围是(A)a|0a6(B)|2,aa或a4(C)|0,6aa或a(D)|24aa答案C【解析】本题主要考查绝对值不等式的基本解法与集合交集的运算,属于中等题。由|x-a|<1得-1b+2}因为AB,所以a+1b-2或a-1b+2,即a-b-3或a-b3,即|a-b|3【温馨提示】处理几何之间的子集、交、并运算时一般利用数轴求解。14.(2010广东理)1.若集合A={x-2<x<1},B={x0<x<2}则集合A ∩B=()A.{x-1<x<1}B.{x-2<x<1}C.{x-2<x<2}D.{x0<x<1}答案D.【解析】{|21}{|02}{|01}ABxxxxxx.15.(2010广东文)10.在集合dcba,,,上定义两种运算和如下abcdaabcdbbbbbccbcb0ddbbd那么da()cA.aB.bC.cD.d解:由上表可知:a(cc),故da()cdac,选A16.(2010广东文)1.若集合3,2,1,0A,4,2,1B则集合BAA.4,3,2,1,0B.4,3,2,1C.2,1D.答案A【解析】并集,选A.17.(2010福建文)1.若集合A=x|1x3,B=x|x>2,则AB等于()A.x|22答案A【解析】AB=x|1x3x|x>2=x|23}(D){x|x-1或x3}答案C【解析】因为集合M=x|x-1|2x|-1x3,全集U=R,所以UCM=x|x<-1x>3或【命题意图】本题考查集合的补集运算,属容易题.22.(2010安徽理)2、若集合121log2Axx,则ARðA、2(,0],2B、2,2C、2(,0][,)2D、2[,)22.A23.(2010湖南理)1.已知集合M={1,2,3},N={2,3,4},则A.MNB.NMC.{2,3}MND.{1,4}MN24.(2010湖北理)2.设集合22{,|1}416xyAxy,{(,)|3}xBxyy,则AB的子集的个数是A.4B.3C.2D.1答案A【解析】画出椭圆221416xy和指数函数3xy图象,可知其有两个不同交点,记为A1、A2,则AB的子集应为1212,,,,AAAA共四种,故选A.二、填空题1.(2010上海文)1.已知集合1,3,Am,3,4B,1,2,3,4AB则m。答案2【解析】考查并集的概念,显然m=22.(2010湖南文)15.若规定E=1,210...aaa的子集12...,nkkkaaa为E的第k个子集,其中k=1211222nkkk,则(1)1,3,aa是E的第____个子集;(2)E的第211个子集是_______答案53.(2010湖南文)9.已知集合A={1,2,3,},B={2,m,4},A∩B={2,3},则m=答案34.(2010重庆理)(12)设U=0,1,2,3,A=20xUxmx,若1,2UA,则实数m=_________.答案-3【解析】1,2UA,A={0,3},故m=-35.(2010江苏卷)1、设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=___________.答案1【解析】考查集合的运算推理。3B,a+2=3,a=1.6.(2010重庆文)(11)设|10,|0AxxBxx,则AB=____________.答案|1|0|10xxxxxx2009年高考题一、选择题1.(2009年广东卷文)已知全集UR,则正确表示集合{1,0,1}M和2|0Nxxx关系的韦恩(Venn)图是()答案B解析由2|0Nxxx,得{1,0}N,则NM,选B.2.(2009全国卷Ⅰ理)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=AB,则集合()uABI中的元素共有()A.3个B.4个C.5个D.6个解:{3,4,5,7,8,9}AB,{4,7,9}(){3,5,8}UABCAB故选A。也可用摩根律:()()()UUUCABCACB答案A3.(2009浙江理)设UR,{|0}Axx,{|1}Bxx,则UABð()A.{|01}xxB.{|01}xxC.{|0}xxD.{|1}xx答案B解析对于1UCBxx,因此UABð{|01}xx4.(2009浙江理)设UR,{|0}Axx,{|1}Bxx,则UABð()A.{|01}xxB.{|01}xxC.{|0}xxD.{|1}xx答案B解析对于1UCBxx,因此UABð{|01}xx.5.(2009浙江文)设UR,{|0}Axx,{|1}Bxx,则UABð()A.{|01}xxB.{|01}xxC.{|0}xxD.{|1}xx答案B【命题意图】本小题主要考查了集合中的补集、交集的知识,在集合的运算考查对于集合理解和掌握的程度,当然也很好地考查了不等式的基本性质.解析对于1UCBxx,因此UABð{|01}xx.6.(2009北京文)设集合21{|2},{1}2AxxBxx,则AB()A.{12}xxB.1{|1}2xxC.{|2}xxD.{|12}xx答案A解析本题主要考查集合的基本运算以及简单的不等式的解法.属于基础知识、基本运算的考查∵1{|2},2Axx2{1}|11Bxxxx,∴{12}ABxx,故选A.7.(2009山东卷理)集合0,2,Aa,21,Ba,若0,1,2,4,16AB,则a的值为()A.0B.1C.2D.4答案D解析∵0,2,Aa,21,Ba,0,1,2,4,16AB∴2164aa∴4a,故选D.【命题立意】:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案本题属于容易题.8.(2009山东卷文)集合0,2,Aa,21,Ba,若0,1,2,4,16AB,则a的值为()A.0B.1C.2D.4答案D解析∵0,2,Aa,21,Ba,0,1,2,4,16AB∴2164aa∴4a,故选D.【命题立意】:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案本题属于容易题.9.(2009全国卷Ⅱ文)已知全集U={1,2,3,4,5,6,7,8},M={1,3,5,7},N={5,6,7},则Cu(MN)=()A.{5,7}B.{2,4}C.{2.4.8}D.{1,3,5,6,7}答案C解析本题考查集合运算能力。10.(2009广东卷理)已知全集UR,集合{212}Mxx和{21,1,2,}Nxxkk的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有()A.3个B.2个C.1个D.无穷多个答案B解析由{212}Mxx得31x,则3,1NM,有2个,选B.11.(2009安徽卷理)若集合21|21|3,0,3xAxxBxx则A∩B是A.11232xxx或B.23xxC.122xxD.112xx答案D解析集合1{|12},{|3}2AxxBxxx或,∴1{|1}2ABxx选D12.(2009安徽卷文)若集合,则是A.{1,2,3}B.{1,2}C.{4,5}D.{1,2,3,4,5}答案B解析解不等式得1|32Axx∵1||5BxxNx∴1,2AB,选B。13.(2009江西卷理)已知全集UAB中有m个元素,()()UUABðð中有n个元素.若ABI非空,则ABI的元素个数为()A.mnB.mnC.nmD.mn答案D解析因为[()()]UUUABABððð,所以AB共有mn个元素,故选D14.(2009湖北卷理)已知{|(1,0)(0,1),},{|(1,1)(1,1),}PaammRQbbnnR是两个向量集合,则PQI()A.{〔1,1〕}B.{〔-1,1〕}C.{〔1,0〕}D.{〔0,1〕}答案A解析因为(1,)(1,1)ambnn代入选项可得1,1PQ故选A.15.(2009四川卷文)设集合S={x|5x},T={x|0)3)(7(xx}.则TS=()A.{x|-7<x<-5}B.{x|3<x<5}C.{x|-5<x<3}D.{x|-7<x<5}答案C解析S={x|55x},T={x|37x}∴TS={x|-5<x<3}16.(2009全国卷Ⅱ理)设集合1|3,|04xAxxBxx,则AB=A.B.3,4C.2,1D.4.答案B解:1|0|(1)(4)0|144xBxxxxxxx.(3,4)AB.故选B.17.(2009福建卷理)已知全集U=R,集合2{|20}Axxx,则UAð等于A.{x∣0x2}B.{x∣02}D.{x∣x0或x2}答案A解析∵计算可得0Axx或2x∴02CuAxx.故选A18.(2009辽宁卷文)已知集合M=﹛x|-3<x5﹜,N=﹛x|x<-5或x>5﹜,则MN=()A.﹛x|x<-5或x>-3﹜B.﹛x|-5<x<5﹜C.﹛x|-3<x<5﹜D.﹛x|x<-3或x>5﹜答案A解析直接利用并集性质求解,或者画出数轴求解.19.(2009宁夏海南卷理)已知集合1,3,5,7,9,0,3,6,9,12AB,则NACBI()A.1,5,7B.3,5,7C.1,3,9D.1,2,3答案A解析易有NACB1,5,7,选A20.(2009陕西卷文)设不等式20xx的解集为M,函数()ln(1||)fxx的定义域为N则MN为()A.[0,1)B.(0,1)C.[0,1]D.(-1,0]答案A.解析[0,1],(1,1)MN,则[0,1)MN,故选A.21.(2009四川卷文)设集合S={x|5x},T={x|0)3)(7(xx}.则TS=()A.{x|-7<x<-5}B.{x|3<x<5}C.{x|-5<x<3}D.{x|-7<x<5}答案C解析S={x|55x},T={x|37x}∴TS={x|-5<x<3}22.(2009全国卷Ⅰ文)设集合A={4,5,6,7,9},B={3,4,7,8,9},全集=AB,则集合[u(AB)中的元素共有A.3个B.4个C.5个D.6个解析本小题考查集合的运算,基础题。(同理1)解:{3,4,5,7,8,9}AB,{4,7,9}(){3,5,8}UABCAB故选A。也可用摩根律:()()()UUUCABCACB23.(2009宁夏海南卷文)已知集合1,3,5,7,9,0,3,6,9,12AB,则ABA.3,5B.3,6C.3,7D.3,9答案D解析集合A与集合B都有元素3和9,故AB3,9,选.D。24.(2009四川卷理)设集合2|5,|4210,SxxTxxx则STA.|75xx B.|35xx C.|53xx D.|75xx【考点定位】本小题考查解含有绝对值的不等式、一元二次不等式,考查集合的运算,基础题。解析:由题)3,7(T),5,5(S,故选择C。解析2:由{|55},Sxx{|73}Txx故{|53}STxx,故选C.25.(2009福建卷文)若集合|0.|3AxxBxx,则AB等于A.{|0}xxB{|03}xxC{|4}xxDR答案B解析本题考查的是集合的基本运算.属于容易题.解法1利用数轴可得容易得答案B.解法2(验证法)去X=1验证.由交集的定义,可知元素1在A中,也在集合B中,故选.二、填空题26.(2009年上海卷理)已知集合|1Axx,|Bxxa,且ABR,则实数a的取值范围是______________________.答案a≤1解析因为A∪B=R,画数轴可知,实数a必须在点1上或在1的左边,所以,有a≤1。27.(2009重庆卷文)若{Unn是小于9的正整数},{AnUn是奇数},{BnUn是3的倍数},则()UABð.答案2,4,8解法1{1,2,3,4,5,6,7,8}U,则{1,3,5,7},{3,6,9},AB所以{1,3,5,7,9}AB,所以(){2,4,8}UABð解析2{1,2,3,4,5,6,7,8}U,而(){|(){2,4,8}UUABnUnABðð28..(2009重庆卷理)若3AxRx,21xBxR,则AB.答案(0,3)解析因为|33,|0,AxxBxx所以(0,3)ABI29..(2009上海卷文)已知集体A={x|x≤1},B={x|≥a},且A∪B=R,则实数a的取值范围是__________________.答案a≤1解析因为A∪B=R,画数轴可知,实数a必须在点1上或在1的左边,所以,有a≤1。30.(2009北京文)设A是整数集的一个非空子集,对于kA,如果1kA且1kA,那么k是A的一个“孤立元”,给定{1,2,3,4,5,6,7,8,}S,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有个.答案6.w解析本题主要考查阅读与理解、信息迁移以及学生的学习潜力,考查学生分析问题和解决问题的能力.属于创新题型.什么是“孤立元”?依题意可知,必须是没有与k相邻的元素,因而无“孤立元”是指在集合中有与k相邻的元素.故所求的集合可分为如下两类:因此,符合题意的集合是:1,2,3,2,3,4,3,4,5,4,5,6,5,6,7,6,7,8共6个.故应填6.31..(2009天津卷文)设全集1lg|*xNxBAU,若4,3,2,1,0,12|nnmmBCAU,则集合B=__________.答案{2,4,6,8}解析}9,8,7,6,5,4,3,2,1{BAU}9,7,5,3,1{BCAU}8,6,4,2{B【考点定位】本试题主要考查了集合的概念和基本的运算能力。32.(2009陕西卷文)某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有人。答案:8.解析:由条件知,每名同学至多参加两个小组,故不可能出现一名同学同时参加数学、物理化学课外探究小组,设参加数学、物理、化学小组的人数构成的集合分别为,,ABC,则()0cardABC.()6,()4cardABcardBC,由公式()()()()()()()cardABCcardAcardBcardCcardABcardACcardBC易知36=26+15+13-6-4-()cardAC故()cardAC=8即同时参加数学和化学小组的有8人.33.(2009湖北卷文)设集合A=(x∣log2x<1),B=(X∣21XX<1),则AB=.答案|01xx解析易得A=|02xxB=|21xx∴A∩B=|01xx.34..(2009湖南卷理)某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_12__答案:12解析设两者都喜欢的人数为x人,则只喜爱篮球的有(15)x人,只喜爱乒乓球的有(10)x人,由此可得(15)(10)830xxx,解得3x,所以1512x,即所求人数为12人。35.(2009湖南卷文)某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为12.解:设所求人数为x,则只喜爱乒乓球运动的人数为10(15)5xx,故15530812xx.注:最好作出韦恩图!2005—2008年高考题一、选择题1.(2008年北京卷1)已知全集UR,集合|23Axx≤≤|14Bxxx或,那么集合A(uB等于()A.|24xx≤B.|34xxx或≤≥C.|21xx≤D.|13xx≤≤答案D2.(2008年四川卷1)设集合1,2,3,4,5,1,2,3,2,3,4UAB,则u)(BA() A.2,3 B.1,4,5 C.4,5 D.1,5答案B3.(2008年全国II理1文)设集合M={mZ|-3<m<2},N={nZ|-1≤n≤3},则MN()A.01,B.101,,C.012,,D.1012,,,答案B解析1,0,1,2M,3,2,1,0,1N,∴1,0,1NM选B.高考考点集合的运算,整数集的符号识别4.(2008年山东卷1)满足M{a1,a2,a3,a4},且M∩{a1,a2,a3}={a1,a2}的集合M的个数是()A.1 B.2C.3D.4答案B5.(2007年全国Ⅰ)设,abR,集合{1,,}{0,,}bababa,则ba()A.1B.1C.2D.2答案C6.(2007年江西)若集合M={0,l,2},N={(x,y)|x-2y+1≥0且x-2y-1≤0,x,y∈M},则N中元素的个数为()A.9B.6C.4D.2答案C7.(2007年安徽)若>122|X-2|log|82xRxBxAZ,则A(RB)的元素个数为()A.0B.1C.2D.3答案C8.(2008年江西卷2)定义集合运算:,,.ABzzxyxAyB设1,2A,0,2B,则集合AB的所有元素之和为()A.0B.2C.3D.6答案D9.(2006年全国II理1文1)已知集合M={x|x<3},N={x|log2x>1},则M∩N=()A.B.{x|0<x<3}C.{x|1<x<3}D.{x|2<x<3}答案D解析2log12Nxxxx,用数轴表示可得答案D。考察知识点有对数函数的单调性,集合的交集。本题比较容易.10.(2005天津卷理)设集合RxxxA,914,RxxxxB,03,则A∩B=()A.]2,3(B.]25,0[]2,3(C.),25[]3,(D.),25[)3,(答案D11.(2005上海)已知集合RxxxM,2|1||,ZxxxP,115|,则PM等于()A.Zxxx,30|B.Zxxx,30|C.Zxxx,01|D.Zxxx,01|答案B二、填空题12.(2007年北京)已知集合1axxA,0452xxxB,若BA,则实数a的取值范围是.答案3,213.(2006年上海卷)已知集合A={-1,3,2m-1},集合B={3,2m}.若BA,则实数m=.答案由2211mmm,经检验,1m为所求;14.(2006年上海卷)已知{1,3,}Am,集合{3,4}B,若BA,则实数___m。答案已知{1,3,}Am,集合{3,4}B,若BA,则实数4m15.(2005年重庆卷理)集合xBxxRxA{},06|{2R|}2|2|x,则BA=.答案(0,3)15.(2005年重庆文)若集合}0)5)(2(|{},034|{2xxRxBxxRxA,则BA.答案(2,3)第二部分四年联考汇编2010年联考题题组二(5月份更新)一、选择题1.(安徽两地三校国庆联考)设合集U=R,集合}1|{},1|{2xxPxxM,则下列关系中正确的是()A.M=PB.MPC.PMD.MP答案C2.(昆明一中一次月考理)设集合2{|320}Mxxx,集合1{|()4}2xNx,则MN()A.{|2}xxB.{|1}xxC.{|1}xxD.{|2}xx答案:A3.(池州市七校元旦调研)设UR,{|0}Axx,{|1}Bxx,则UABð()A.{|01}xxB.{|01}xxC.{|0}xxD.{|1}xx答案:B解析对于1UCBxx,因此UABð{|01}xx.4.(昆明一中一次月考理)定义映射f:A→B,若集合A中元素x在对应法则f作用下的象为3logx,则A中元素9的象是()A.3B.2C.2D.3答案:C5.(岳野两校联考)若P={1、2、3、4、5},Q={0、2、3},且定义AB{|xAx且Bx},那么()()PQQP()A.B.{0、1、2、3、4、5}C{0}D{0、1、4、5}答案D6.(昆明一中一次月考理)设1a,集合103xAxx,210Bxxaxa。若AB,则a的取值范围是()A.13aB.3aC.3aD.13a答案:B7.(安徽两地三校国庆联考)设集合A={x|11xx<0},B={x||x-1|<a},若“a=1”是“A∩B≠φ”的(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分又不必要条件答案A8.(昆明一中四次月考理)已知集合2log(1)0Sxx,202xTxx,则ST等于()(A)0,2(B)1,2(C)1,(D)2,答案:D9.(安徽六校联考)若集合{||2|1}Axx,2{|0}21xBxx,则AB()A.1{|2}2xxB.{|23}xxC.11{|1}22xxx或D.1{|3}2xx答案B10.(哈师大附中、东北师大附中、辽宁省实验中学)若集合1,2,3,4,2ABxNx,则AB()A.1,2,3,4B.2,1,0,1,2,3,4C.1,2D.2,3,4答案C11.(玉溪一中期中文)已知2{|4}Axx,3{|log1}Bxx,则AB=()A.{|2}xxB.{|23}xxC.{|3}xxD.{|2}{|23}xxxx答案:B二、填空题1.(安庆市四校元旦联考)设集合{|1Ax≤x≤2},B={x|0≤x≤4},则A∩B=.答案[0,2]2.(安徽两地三校国庆联考)已知集合P={(x,y)|y=m},Q={(x,y)|y=1xa,a>0,a≠1},如果PQ有且只有一个元素,那么实数m的取值范围是________.答案m>13.设命题P:2aa,命题Q:对任何xR,都有2410xax.命题P与Q中有且仅有一个成立,则实数a的取值范围是.答案021a或121a解:由aa2得10a.由0142axx对于任何xR成立,得04162a,即2121a.因为命题P、Q有且仅有一个成立,故实数a的取值范围是021a或121a.三、解答题1.(本小题满分10分)(安徽两地三校国庆联考)设命题P:关于x的不等式a222aaxx>1(a>0且a≠1)为{x|-a1/2;P、Q中有且仅有一个为真∴0.∴13|xxBA(II){}44Axaxa=-<<+.{}15Bxxx或=<->.且RBA315414aaa实数a的取值范围是()1,3.2007---2008年联考题一、选择题1.(广东地区2008年01月份期末试题汇编)设全集U=R,A={x∈N︱1≤x≤10},B={x∈R︱x2+x-6=0},则下图中阴影表示的集合为()A.{2}B.{3}C.{-3,2}D.{-2,3}答案A2.(2007-2008年湖南示范)已知M={y|y=x2},N={y|x2+y2=2},则MN=()A、{(1,1),(-1,1)}B、{1}C、[0,1]D、[0,2]答案D解析M={y|y≥0},N={x|-2≤x≤2},选D(注意:集合表示的是范围不是点)3.(广东地区2008年01月份期末试题汇编)已知全集U=R,集合|1Axyx,集合|0Bx<x<2,则()UCAB()A.1,)B.1,C.0),+D.0,+答案D4.(2008年江苏省启东中学高三综合测试二)定义集合A*B={x|xA,且xB},若A={1,3,5,7},B={2,3,5},则A*B的子集个数为()A.1B.2C.3D.4答案D5.(广东地区2008年01月份期末试题汇编)设全集{0,1,2,3,4}U,集合{0,1,2}A,集合{2,3}B,则()UABð( )A.B.{1,2,3,4}C.{0,1,2,3,4}D.{2,3,4}答案D6.(广东地区2008年01月份期末试题汇编)设集合{1,2}M,则满足条件{1,2,3,4}MN的集合N的个数是( )A.1B.3C.4D.8答案C7.(2007-2008北京四中模三文)设全集U=R,集合2|{2xxxM,R}x,21|{xxN,R}x则NMCU)(等于( )A.{2} B.}31|{xx C.{x|x<2,或2<x<3} D.21|{xx或}32x答案D解析M={2},N=[-1,3],CUM=(-∞,2)∪(2,+∞),选D8.(广东地区2008年01月份期末试题汇编)设全集,UR且|12Axx,2|680Bxxx,则()UCAB()A.[1,4)B.(2,3)C.(2,3]D.(1,4)答案C9.(黄爱民,胡彬《中学生学习报》2005模拟一)设集合I={1,2,3},AI,若把集合M∪A=I的集合M叫做集合A的配集,则A={1,2}的配集有()个A,1B,2C,3D,4答案D解析分A的配集中一定含有元素3,余下两个元素1,2可以全不含、仅有一个、两个都有;选D10.(广东地区2008年01月份期末试题汇编)设集合A=2{|21},{|ln(1)}xxBxyx,则AB为()A.{|2}xxB.{|12}xxC.{|1}xxD.{|1}xx答案C解析(,2),(,1)AB则(,1)AB选C.11.(广东地区2008年01月份期末试题汇编)设全集U=R,A=(2){|21},{|ln(1)}xxxBxyx,则右图中阴影部分表示的集合为A.{|1}xxB.{|12}xxC.{|01}xxD.{|1}xx答案B解析(0,2),(,1)AB,图中阴影部分表示的集合为[1,2)UABð,选B.12.(广东地区2008年01月份期末试题汇编)设集合{1,2}A,则满足{1,2,3}AB的集合B的个数是()。A.1B.3C.4D.8答案C解析{1,2}A,{1,2,3}AB,则集合B中必含有元素3,即此题可转化为求集合{1,2}A的子集个数问题,所以满足题目条件的集合B共有224个。故选择答案C。13.(广东地区2008年01月份期末试题汇编)集合2,4,6M的真子集的个数为A.6B.7C.8D.9答案B14.(2008年广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)设全集U=R,A={x∈N︱1≤x≤10},B={x∈R︱x2+x-6=0},则下图中阴影表示的集合为()A.{2}B.{3}C.{-3,2}D.{-2,3}答案Aw.w.w.15.(广东地区2008年01月份期末试题汇编)已知集合2{|log1},{|1}MxxNxx,则MN=().A.{|01}xxB.{|02}xxC.{|1}xxD.16.(广东地区2008年01月份期末试题汇编)已知I为实数集,2{|20},{|1}MxxxNxyx,则I()MNð=().A.{|01}xxB.{|02}xxC.{|1}xxD.17.(2007-2008燕园冲刺三)年集合P={1,4,9,16,……},若a∈P,b∈P,有a○b∈P,则运算○可能是()A,加法B,减法C,除法D,乘法答案D解析P={n2},ab∈P,选D18.(广东地区2008年01月份期末试题汇编)设(,)46,(,)38AxyyxBxyyx,则ABB.(2,1).(2,2).(3,1).(4,2).ABCD19.(2007年岳阳市一中高三训练)a、b为实数,集合xxfaNabM:},0,{},1,{表示把集合M中的元素x映射到集合N中仍为x,则ba=()A、1B、0C、-1D、±1答案A20.(广东地区2008年01月份期末试题汇编)设全集I={-2,-1,-21,31,21,1,2,3},A={31,21,1,2,3},B={-2,2},则集合{-2}等于()A.A∩BB.IA∩BC.IA∩IBD.A∪IB答案B21.(广东地区2008年01月份期末试题汇编)若集合}1|{2xxM,}1|{xxyxN,则NM=A.MB.NC.D.}10|{}01|{xxxx答案B解析本题考查了定义域及交集运算M={|x-1<x<1},N={|x0≤x<1}22.(2007年岳阳市一中高三训练)a、b为实数,集合xxfaNabM:},0,{},1,{表示把集合M中的元素x映射到集合N中仍为x,则ba=()A、1B、0C、-1D、±1答案A23.(广东地区2008年01月份期末试题汇编)设I是全集,I={0,1,2,3,4},集合A={0,l,2,3},集合B={4},则BCACII()A.{0}B.{0,1}C.{0,1,2,3,4}D.{0,1,4}答案C24.(湖北省黄冈中学2007年高三年级4月)对于函数)]([)(,)],([)()],([)(11)(1232xffxfxffxfxffxfxxxfnn,设)2*,(nNn且,令集合},)(|{2007RxxxfxM,则集合M为()A.空集B.实数集C.单元素集D.二元素集答案A二、填空题24.(2007-2008北京四中模二文)已知集合P={(x,y)|y=m},Q={(x,y)|y=1xa,a>0,a≠1},如果PQ有且只有一个元素,那么实数m的取值范围是________解析Q={y|y>1},所以m>1。填m>125.(2007-2008江苏常州模拟)设含有集合A={1,2,4,8,16}中三个元素的集合A的所有子集记为B1,B2,B3,…,Bn(其中n∈N*),又将Bk(k=1,2,……,n)的元素之和记为ak,则nkka1=_____解析五个元素中,每个元素都出现C24=6次,nkka1=6×(1+2+4+8+16)=186,填18626.(2008年江苏省启东中学高三综合测试一)满足0,1,2{0,1,2,3,4,5}A的集合A的个数是_______个。答案727.(2008年北京市宣武区高三综合练习一)设集合A=Rxxx,22,B=30,222xxxyy,则R(BA)=.答案(-∞,1)∪(4,+∞)28.(2008年北京市宣武区高三综合练习二)对任意两个集合M、N,定义:NxMxxNM且,MNNMNM,RxxyyM,2,RxxyyN,sin3,则NM.答案[-3,0)∪(3,+∞)29.(2007~2008学年福建省莆田一中上学期期末考试卷)非空集合G关于运算满足:①对于任意a、bG,都有abG;②存在Ge,使对一切Ga都有ae=ea=a,则称G关于运算为融洽集,现有下列集合运算:⑴G={非负整数},为整数的加法⑵G={偶数},为整数的乘法⑶G={平面向量},为平面向量的加法⑷G={二次三项式},为多项式的加法其中关于运算的融洽集有____________答案⑴⑵⑶三、解答题30.(2008年河南省上蔡一中高三月考)已知函数1()2xfxx的定义域集合是A,函数22()lg[(21)]gxxaxaa的定义域集合是B(1)求集合A、B(2)若AB=B,求实数a的取值范围.解(1)A=|12xxx或B=|1xxaxa或(2)由AB=B得AB,因此112aa所以11a,所以实数a的取值范围是1,1展开内容










 小学二年级数学期中考试试卷word
小学二年级数学期中考试试卷word 2014年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析
2014年全国统一高考数学试卷(文科)(新课标ⅱ)+参考答案解析 小学二年级数学乘法口算题+答案(word版)
小学二年级数学乘法口算题+答案(word版) 2017年高考数学知识方法专题11《数学方法第49练 配凑法与构造法》
2017年高考数学知识方法专题11《数学方法第49练 配凑法与构造法》 2009年上海高考数学(理科)试卷+(word解析版答案)
2009年上海高考数学(理科)试卷+(word解析版答案)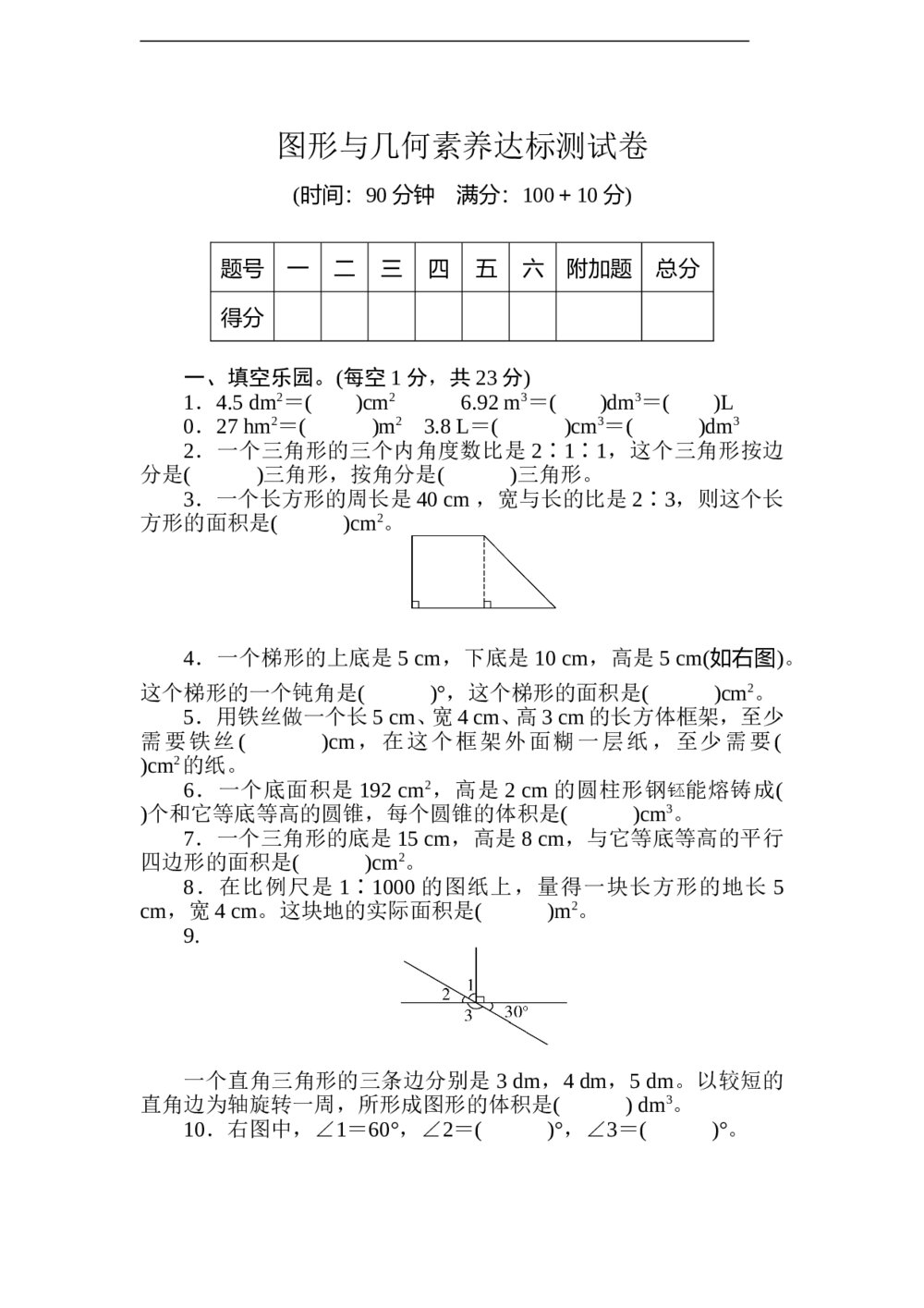 人教版六年级数学下册《图形与几何素养》达标测试卷word版+(答案)
人教版六年级数学下册《图形与几何素养》达标测试卷word版+(答案)