









试读已结束,还剩2页未读,您可下载完整版后进行离线阅读
《2012年朝阳区高三二模数学(理科)试卷+答案》是由用户上传到老师板报网,本为文库资料,大小为579.5 KB,总共有12页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 12页
- 579.5 KB
- VIP模板
- doc
- 数字产品不支持退货
北京市朝阳区2011-2012学年度高三年级第二次综合练习数学试卷(理工类)2012.5(考试时间120分钟满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知全集RU,集合21xAx,2340Bxxx,则UABð=A.04xxB.04xxC.10xxD.14xx2.复数z满足等式(2i)iz,则复数z在复平面内对应的点所在的象限是A.第一象限B.第二象限C.第三象限D.第四象限3.已知双曲线2215xym(0m)的右焦点与抛物线212yx的焦点相同,则此双曲线的离心率为A.6B.322C.32D.344.在△ABC中,2AB,3AC,0ABAC,且△ABC的面积为32,则BAC等于A.60或120B.120C.150D.30或1505.在直角坐标系xOy中,直线l的参数方程为,4xtyt(t为参数).以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为42sin()4,则直线l和曲线C的公共点有A.0个B.1个C.2个D.无数个6.下列命题::p函数44()sincosfxxx的最小正周期是;:q已知向量(1),=a,2(1),=-b,(11),=c,则(+)//abc的充要条件是1;:r若111adx=x(1a),则ea.其中所有的真命题是A.rB.,pqC.,qrD.,pr7.直线yx与函数22,,()42,xmfxxxxm的图象恰有三个公共点,则实数m的取值范围是A.[1,2)B.[1,2]C.[2,)D.(,1]8.有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是A.1B.322C.2D.3第二部分(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.二项式251(+)axx展开式中的常数项为5,则实数a=_______.10.执行如图所示的程序框图,输出的结果是_______.x=1,y=1,z=2z≤10开始结束是否z=x+y输出zy=zx=y(第10题图)11.若实数,xy满足10,0,xyx则22xy的最小值是.12.如图,AB是圆O的直径,CDAB于D,且2ADBD,E为AD的中点,连接CE并延长交圆O于F.若2CD,则AB_______,EF_________.13.一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(xN)件.当20x时,年销售总收入为(233xx)万元;当20x时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元,则y(万元)与x(件)的函数关系式为,该工厂的年产量为件时,所得年利润最大.(年利润=年销售总收入年总投资)14.在如图所示的数表中,第i行第j列的数记为,ija,且满足11,,12,jjiaai,1,1,1,(,)Nijijijaaaij,则此数表中的第5行第3列的数是;记第3行的数3,5,8,13,22,为数列{}nb,则数列{}nb的通项公式为.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上.15.(本小题满分13分)已知函数23sincoscosfxxxxm()Rm的图象过点π(,0)12M.(Ⅰ)求m的值;(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c.若cos+cos=2coscBbCaB,第1行1248…第2行2359…第3行35813………CFBAEDO求()fA的取值范围.16.(本小题满分13分)一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率;(Ⅱ)求取出的3个球中恰有2个球编号相同的概率;(Ⅲ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.]17.(本小题满分14分)在如图所示的几何体中,四边形ABCD为正方形,EA平面ABCD,//EFAB,=4,=2,=1ABAEEF.(Ⅰ)若点M在线段AC上,且满足14CMCA,求证://EM平面FBC;(Ⅱ)求证:AF平面EBC;(Ⅲ)求二面角--AFBD的余弦值.18.(本小题满分14分)已知函数22()ln(0)afxaxxax.(Ⅰ)若曲线()yfx在点(1,(1))f处的切线与直线20xy垂直,求实数a的值;(Ⅱ)讨论函数()fx的单调性;(Ⅲ)当(,0)a时,记函数()fx的最小值为()ga,求证:21()e2ga.19.(本小题满分13分)在平面直角坐标系xOy中,已知点(2,0)A,(2,0)B,E为动点,且直线EA与直线EB的斜率之积为12.(Ⅰ)求动点E的轨迹C的方程;(Ⅱ)设过点(1,0)F的直线l与曲线C相交于不同的两点M,N.若点P在y轴上,且PMPN,求点P的纵坐标的取值范围.20.(本小题满分13分)已知数列12:,,,nnAaaa(,2)nn*N满足01naa,且当nk2()*Nk时ECBDMAF,1)(21kkaa,令1()nniiSAa.(Ⅰ)写出)(5AS的所有可能的值;(Ⅱ)求)(nAS的最大值;(Ⅲ)是否存在数列nA,使得2(3)()4nnSA?若存在,求出数列nA;若不存在,说明理由.北京市朝阳区高三年级第二次综合练习数学答案(理工类)2012.5一、选择题:题号12345678答案BBCCBDAD二、填空题:9.110.1311.1212.3,23313.2**32100,020,,160,20,,NNxxxxyxxx1614.16,121nnan三、解答题:15.(本小题满分13分)解:(Ⅰ)由31sin2(cos21)22fxxxmπ1sin(2)62xm.……3分因为点π(,0)12M在函数fx的图象上,所以ππ1sin(2)01262m,解得12m.……5分(Ⅱ)因为cos+cos=2coscBbCaB,所以sincossincosCBBC=2sincosAB,所以sin(+)2sincosBCAB,即sin2sincosAAB.……7分又因为(0,A,所以sin0A,所以1cos2B.……8分又因为(0,B,所以π3B,2π3AC.……10分所以2π03A,ππ7π2666A,所以πsin(2)6A1(,1]2.…12分所以()fA的取值范围是1(,1]2.……13分16.(本小题满分13分)解:(Ⅰ)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,则39325()84PAC.答:取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为584.…4分[](Ⅱ)设“取出的3个球中恰有两个球编号相同”为事件B,则114739281()843CCPBC.答:取出的3个球中恰有两个球编号相同的概率为13.……8分(Ⅲ)X的取值为2,3,4,5.12212222391(2)21CCCCPXC,12212424394(3)21CCCCPXC,12212626393(4)7CCCCPXC,1218391(5)3CCPXC.……11分所以X的分布列为X2345P1214213713X的数学期望143185234521217321EX.……13分17.(本小题满分14分)证明:(Ⅰ)过M作MNBC于N,连结FN,则MN//AB,又14CMAC,所以14MNAB.又EF//AB且14EFAB,所以EF//MN,且EFMN,所以四边形EFNM为平行四边形,所以EM//FN.又FN平面FBC,EM平面FBC,所以//EM平面FBC.……4分(Ⅱ)因为EA平面ABCD,ABAD,故以A为原点,建立如图所示的空间直角坐标系-Axyz.由已知可得(0,0,0),(4,0,0),(4,4,0),(0,4,0),ABCD(0,0,2),(1,0,2)EF.EDCMAFBNxzECBDMAFy显然=(1,0,2),=(0,4,0),=(4,0,-2)AFBCEB.则=0,=0AFBCAFEB,所以,AFBCAFEB.即,AFBCAFEB,故AF平面EBC.(Ⅲ)因为EF//AB,所以EF与AB确定平面EABF,由已知得,=(0,4,0),=(3,0,-2)BCFB,=(4,4,0)-BD.……9分因为EA平面ABCD,所以EABC.由已知可得ABBC且=EAABA,所以BC平面ABF,故BC是平面ABF的一个法向量.设平面DFB的一个法向量是()nx,y,z.由0,0,nnBDFB得440,320,xyxz即32yx,zx,令2x,则(2,2,3)n.所以217cos<17,nnnBCBCBC.由题意知二面角A-FB-D锐角,故二面角A-FB-D的余弦值为21717.……14分18.(本小题满分14分)解:(I)fx的定义域为{|0}xx.22210aafxxxx.根据题意,有12f,所以2230aa,解得1a或32a.……3分(II)22222222()(2)10aaxaxaxaxafxxxxxx.(1)当0a时,因为0x,由()0fx得()(2)0xaxa,解得xa;由()0fx得()(2)0xaxa,解得0xa.所以函数()fx在,a上单调递增,在0,a上单调递减.(2)当0a时,因为0x,由()0fx得()(2)0xaxa,解得2xa;由()0fx得()(2)0xaxa,解得02xa.所以函数()fx在0,2a上单调递减,在2,a上单调递增.……9分(III)由(Ⅱ)知,当(,0)a时,函数()fx的最小值为()ga,且22()(2)ln(2)2ln(2)32agafaaaaaaaa.2()ln(2)3ln(2)22gaaaaa,令()0ga,得21e2a.当a变化时,ga,ga的变化情况如下表:a21(,e)221e221(e,0)2ga+0-ga极大值21e2是()ga在(,0)上的唯一极值点,且是极大值点,从而也是()ga的最大值点.所以22221111(e)eln[2(e)]3(e)2222最大值gag2222131elneee222.所以,当(,0)a时,21()e2ga成立.……14分19.(本小题满分13分)解:(Ⅰ)设动点E的坐标为(,)xy,依题意可知1222yyxx,整理得221(2)2xyx.所以动点E的轨迹C的方程为221(2)2xyx.………5分(II)当直线l的斜率不存在时,满足条件的点P的纵坐标为0.………6分当直线l的斜率存在时,设直线l的方程为(1)ykx.将(1)ykx代入2212xy并整理得,2222(21)4220kxkxk.2880k.设11(,)Mxy,22(,)Nxy,则2122421kxxk,21222221kxxk.设MN的中点为Q,则22221Qkxk,2(1)21QQkykxk,所以2222(,)2121kkQkk.………9分由题意可知0k,又直线MN的垂直平分线的方程为22212()2121kkyxkkk.令0x解得211212Pkykkk..………10分当0k时,因为1222kk,所以120422Py;当0k时,因为1222kk,所以120422Py..………12分综上所述,点P纵坐标的取值范围是22[,]44..………13分20.(本小题满分13分)解:(Ⅰ)由题设,满足条件的数列5A的所有可能情况有:(1)01210,,,,.此时5()=4SA;(2)01010,,,,.此时5()=2SA;(3)01010,,,,.此时5()=0SA;(4)01210,,,,.此时5()=4SA;(5)01010,,,,.此时5()=0SA;(6)01010,,,,.此时5()=2SA;所以,)(5AS的所有可能的值为:4,2,0,2,4.……4分(Ⅱ)由1)(21kkaa,可设11kkkaac,则11kc或11kc(nk2,k*N),因为11nnnaac,所以11221nnnnnnaacacc11221nnacccc.因为01naa,所以1210nccc,且n为奇数,121,,,nccc是由21n个1和21n个1构成的数列.所以112121()()()nnSAcccccc1221(1)(2)2nnncnccc.则当121,,,nccc的前21n项取1,后21n项取1时)(nAS最大,此时)(nAS11(1)(2)(21)22nnnn2(1)4n.证明如下:假设121,,,nccc的前21n项中恰有t项12,,tmmmccc取1,则121,,,nccc的后21n项中恰有t项12,,,tnnnccc取1,其中112nt,112inm,112innn,1,2,,it.所以()nSA1211212211(1)(2)222nnnnnnncnccccc11(1)(2)(21)22nnnn122[()()()]tnmnmnm122[()()()]tnnnnnn221(1)(1)2()44tiiinnnm.所以)(nAS的最大值为2(1)4n.……9分(Ⅲ)由(Ⅱ)可知,如果121,,,nccc的前21n项中恰有t项12,,,tmmmccc取1,121,,,nccc的后21n项中恰有t项12,,,tnnnccc取1,则21(1)()2()4tniiinSAnm,若2(3)()4nnSA,则122()tiiinnm,因为n是奇数,所以2n是奇数,而12()tiiinm是偶数,因此不存在数列nA,使得4)3()(2nASn.……13分展开内容










 2017年高考数学考前回扣教材7《解析几何》
2017年高考数学考前回扣教材7《解析几何》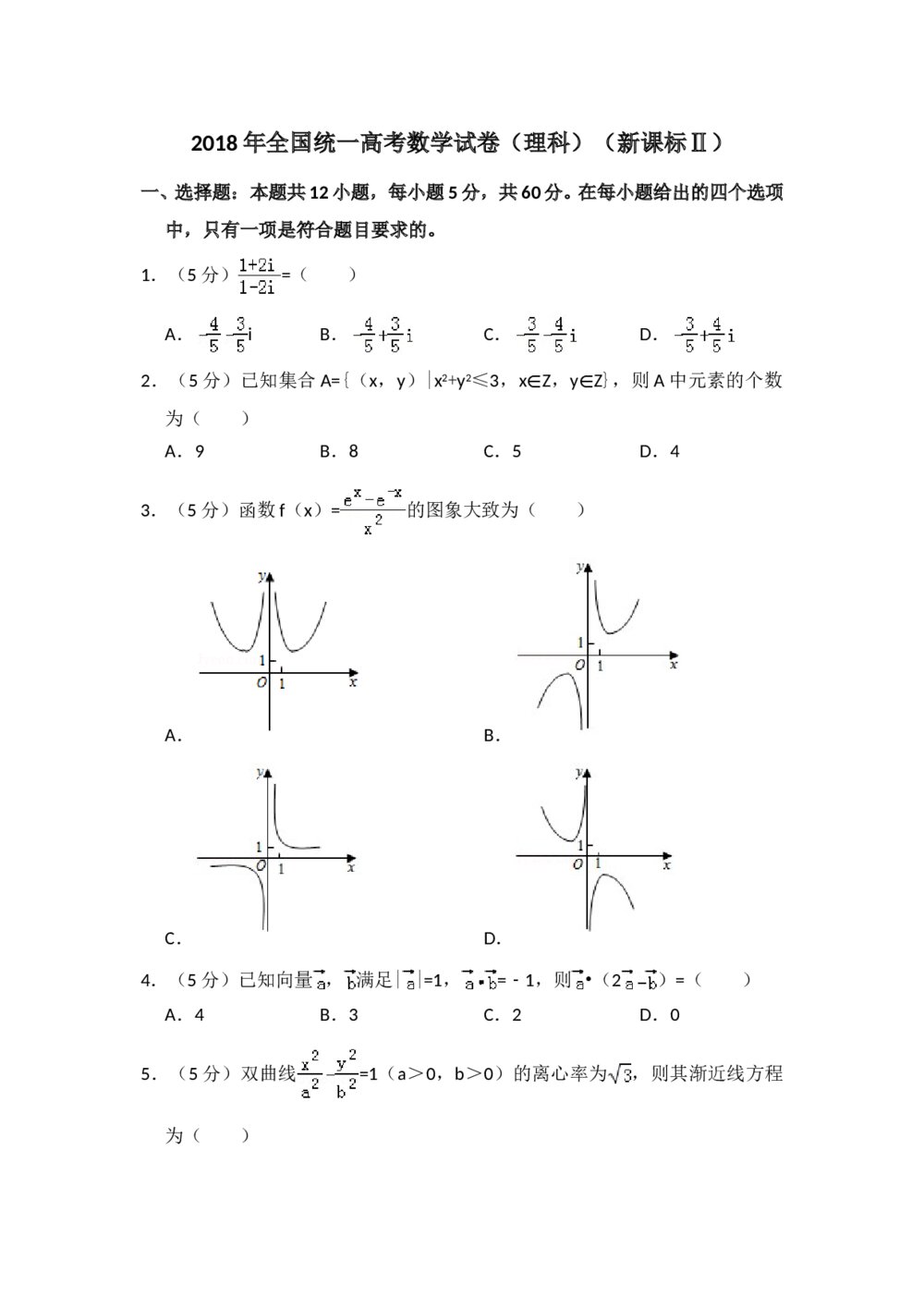 2018年全国统一高考数学试卷(理科)(新课标ⅱ)+参考答案解析
2018年全国统一高考数学试卷(理科)(新课标ⅱ)+参考答案解析 2021年北京市高考数学试题试卷(原卷板)+(参考答案解析)
2021年北京市高考数学试题试卷(原卷板)+(参考答案解析) 九年级数学期末试卷+试卷答案(word版)
九年级数学期末试卷+试卷答案(word版) 2012陕西省高考(文科)数学试卷+答案(文数)word版
2012陕西省高考(文科)数学试卷+答案(文数)word版 2011年高考一轮课时训练(理)6.2等差数列+参考答案(通用版)
2011年高考一轮课时训练(理)6.2等差数列+参考答案(通用版)