









试读已结束,还剩19页未读,您可下载完整版后进行离线阅读
《2013年全国统一高考数学试卷(文科)(新课标ⅰ)+参考答案解析》是由用户上传到老师板报网,本为文库资料,大小为374 KB,总共有29页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 29页
- 374 KB
- VIP模板
- doc
- 数字产品不支持退货
2013年全国统一高考数学试卷(文科)(新课标Ⅰ)一、选择题共12小题.每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项.1.(5分)已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=( )A.{1,4}B.{2,3}C.{9,16}D.{1,2}2.(5分)=( )A.﹣1﹣iB.﹣1+iC.1+iD.1﹣i3.(5分)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )A.B.C.D.4.(5分)已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为( )A.y=B.y=C.y=±xD.y=5.(5分)已知命题p:∀x∈R,2x<3x;命题q:∃x∈R,x3=1x﹣2,则下列命题中为真命题的是( )A.p∧qB.¬p∧qC.p∧¬qD.¬p∧¬q6.(5分)设首项为1,公比为的等比数列{an}的前n项和为Sn,则( )A.Sn=2an1﹣B.Sn=3an2﹣C.Sn=43a﹣nD.Sn=32a﹣n7.(5分)执行程序框图,如果输入的t∈[1﹣,3],则输出的s属于( )A.[3﹣,4]B.[5﹣,2]C.[4﹣,3]D.[2﹣,5]8.(5分)O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为( )A.2B.2C.2D.49.(5分)函数f(x)=(1cosx﹣)sinx在[π﹣,π]的图象大致为( )A.B.C.D.10.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos2A=0,a=7,c=6,则b=( )A.10B.9C.8D.511.(5分)某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π12.(5分)已知函数f(x)=,若|f(x)|≥ax,则a的取值范围是( )A.(﹣∞,0]B.(﹣∞,1]C.[2﹣,1]D.[2﹣,0] 二.填空题:本大题共四小题,每小题5分.13.(5分)已知两个单位向量,的夹角为60°,=t+(1t﹣).若•=0,则t= .14.(5分)设x,y满足约束条件,则z=2xy﹣的最大值为 .15.(5分)已知H是球O的直径AB上一点,AH:HB=1:2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为 .16.(5分)设当x=θ时,函数f(x)=sinx2cosx﹣取得最大值,则cosθ=. 三.解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知等差数列{an}的前n项和Sn满足S3=0,S5=5﹣.(Ⅰ)求{an}的通项公式;(Ⅱ)求数列{}的前n项和.18.(12分)为了比较两种治疗失眠症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:服用A药的20位患者日平均增加的睡眠时间:0.61.22.71.52.81.82.22.33.23.52.52.61.22.71.52.93.03.12.32.4服用B药的20位患者日平均增加的睡眠时间:3.21.71.90.80.92.41.22.61.31.41.60.51.80.62.11.12.51.22.70.5(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?19.(12分)如图,三棱柱ABCA﹣1B1C1中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C;(Ⅱ)若AB=CB=2,A1C=,求三棱柱ABCA﹣1B1C1的体积.20.(12分)已知函数f(x)=ex(ax+b)﹣x24x﹣,曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4.(Ⅰ)求a,b的值;(Ⅱ)讨论f(x)的单调性,并求f(x)的极大值.21.(12分)已知圆M:(x+1)2+y2=1,圆N:(x1﹣)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.请考生在第22、23、24三题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑。22.(10分)(选修41﹣:几何证明选讲)如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.(Ⅰ)证明:DB=DC;(Ⅱ)设圆的半径为1,BC=,延长CE交AB于点F,求△BCF外接圆的半径.23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).24.已知函数f(x)=|2x1﹣|+|2x+a|,g(x)=x+3.(Ⅰ)当a=2﹣时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当x∈[﹣,]时,f(x)≤g(x),求a的取值范围. 2013年全国统一高考数学试卷(文科)(新课标Ⅰ)参考答案与试题解析 一、选择题共12小题.每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项.1.(5分)已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=( )A.{1,4}B.{2,3}C.{9,16}D.{1,2}【考点】1E:交集及其运算.菁优网版权所有【专题】5J:集合.【分析】由集合A中的元素分别平方求出x的值,确定出集合B,找出两集合的公共元素,即可求出交集.【解答】解:根据题意得:x=1,4,9,16,即B={1,4,9,16},∵A={1,2,3,4},∴A∩B={1,4}.故选:A.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键. 2.(5分)=( )A.﹣1﹣iB.﹣1+iC.1+iD.1﹣i【考点】A5:复数的运算.菁优网版权所有【专题】11:计算题.【分析】利用分式的分母平方,复数分母实数化,运算求得结果.【解答】解:====1﹣+i.故选:B.【点评】本题考查复数代数形式的混合运算,复数的乘方运算,考查计算能力. 3.(5分)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )A.B.C.D.【考点】CC:列举法计算基本事件数及事件发生的概率.菁优网版权所有【专题】5I:概率与统计.【分析】本题是一个等可能事件的概率,试验发生包含的事件是从4个不同的数中随机的抽2个,共有C42种结果,满足条件的事件是取出的数之差的绝对值等于2的有两种,得到概率.【解答】解:由题意知本题是一个等可能事件的概率,试验发生包含的事件是从4个不同的数中随机的抽2个,共有C42=6种结果,满足条件的事件是取出的数之差的绝对值等于2,有2种结果,分别是(1,3),(2,4),∴要求的概率是=.故选:B.【点评】本题考查等可能事件的概率,是一个基础题,本题解题的关键是事件数是一个组合数,若都按照排列数来理解也可以做出正确的结果. 4.(5分)已知双曲线C:(a>0,b>0)的离心率为,则C的渐近线方程为( )A.y=B.y=C.y=±xD.y=【考点】KC:双曲线的性质.菁优网版权所有【专题】5D:圆锥曲线的定义、性质与方程.【分析】由离心率和abc的关系可得b2=4a2,而渐近线方程为y=±x,代入可得答案.【解答】解:由双曲线C:(a>0,b>0),则离心率e===,即4b2=a2,故渐近线方程为y=±x=x,故选:D.【点评】本题考查双曲线的简单性质,涉及的渐近线方程,属基础题. 5.(5分)已知命题p:∀x∈R,2x<3x;命题q:∃x∈R,x3=1x﹣2,则下列命题中为真命题的是( )A.p∧qB.¬p∧qC.p∧¬qD.¬p∧¬q【考点】2E:复合命题及其真假.菁优网版权所有【专题】21:阅读型;5L:简易逻辑.【分析】举反例说明命题p为假命题,则¬p为真命题.引入辅助函数f(x)=x3+x21﹣,由函数零点的存在性定理得到该函数有零点,从而得到命题q为真命题,由复合命题的真假得到答案.【解答】解:因为x=1﹣时,21﹣>31﹣,所以命题p:∀x∈R,2x<3x为假命题,则¬p为真命题.令f(x)=x3+x21﹣,因为f(0)=1﹣<0,f(1)=1>0.所以函数f(x)=x3+x21﹣在(0,1)上存在零点,即命题q:∃x∈R,x3=1x﹣2为真命题.则¬p∧q为真命题.故选:B.【点评】本题考查了复合命题的真假,考查了指数函数的性质及函数零点的判断方法,解答的关键是熟记复合命题的真值表,是基础题. 6.(5分)设首项为1,公比为的等比数列{an}的前n项和为Sn,则( )A.Sn=2an1﹣B.Sn=3an2﹣C.Sn=43a﹣nD.Sn=32a﹣n【考点】89:等比数列的前n项和.菁优网版权所有【专题】54:等差数列与等比数列.【分析】由题意可得数列的通项公式,进而可得其求和公式,化简可得要求的关系式.【解答】解:由题意可得an=1×=,∴Sn==3﹣=32﹣=32a﹣n,故选:D.【点评】本题考查等比数列的求和公式和通项公式,涉及指数的运算,属中档题 7.(5分)执行程序框图,如果输入的t∈[1﹣,3],则输出的s属于( )A.[3﹣,4]B.[5﹣,2]C.[4﹣,3]D.[2﹣,5]【考点】3B:分段函数的解析式求法及其图象的作法;EF:程序框图.菁优网版权所有【专题】27:图表型;5K:算法和程序框图.【分析】本题考查的知识点是程序框图,分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算一个分段函数的函数值,由条件为t<1我们可得,分段函数的分类标准,由分支结构中是否两条分支上对应的语句行,我们易得函数的解析式.【解答】解:由判断框中的条件为t<1,可得:函数分为两段,即t<1与t≥1,又由满足条件时函数的解析式为:s=3t;不满足条件时,即t≥1时,函数的解析式为:s=4tt﹣2故分段函数的解析式为:s=,如果输入的t∈[1﹣,3],画出此分段函数在t∈[1﹣,3]时的图象,则输出的s属于[3﹣,4].故选:A.【点评】要求条件结构对应的函数解析式,要分如下几个步骤:①分析流程图的结构,分析条件结构是如何嵌套的,以确定函数所分的段数;②根据判断框中的条件,设置分类标准;③根据判断框的“是”与“否”分支对应的操作,分析函数各段的解析式;④对前面的分类进行总结,写出分段函数的解析式. 8.(5分)O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为( )A.2B.2C.2D.4【考点】K8:抛物线的性质.菁优网版权所有【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.【分析】根据抛物线方程,算出焦点F坐标为().设P(m,n),由抛物线的定义结合|PF|=4,算出m=3,从而得到n=,得到△POF的边OF上的高等于2,最后根据三角形面积公式即可算出△POF的面积.【解答】解:∵抛物线C的方程为y2=4x∴2p=4,可得=,得焦点F()设P(m,n)根据抛物线的定义,得|PF|=m+=4,即m+=4,解得m=3∵点P在抛物线C上,得n2=4×3=24∴n==∵|OF|=∴△POF的面积为S=|OF|×|n|==2故选:C.【点评】本题给出抛物线C:y2=4x上与焦点F的距离为4的点P,求△POF的面积.着重考查了三角形的面积公式、抛物线的标准方程和简单几何性质等知识,属于基础题. 9.(5分)函数f(x)=(1cosx﹣)sinx在[π﹣,π]的图象大致为( )A.B.C.D.【考点】3A:函数的图象与图象的变换.菁优网版权所有【专题】51:函数的性质及应用.【分析】由函数的奇偶性可排除B,再由x∈(0,π)时,f(x)>0,可排除A,求导数可得f′(0)=0,可排除D,进而可得答案.【解答】解:由题意可知:f(﹣x)=(1cosx﹣)sin(﹣x)=f﹣(x),故函数f(x)为奇函数,故可排除B,又因为当x∈(0,π)时,1cosx﹣>0,sinx>0,故f(x)>0,可排除A,又f′(x)=(1cosx﹣)′sinx+(1cosx﹣)(sinx)′=sin2x+cosxcos﹣2x=cosxcos2x﹣,故可得f′(0)=0,可排除D,故选:C.【点评】本题考查三角函数的图象,涉及函数的奇偶性和某点的导数值,属基础题. 10.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos2A=0,a=7,c=6,则b=( )A.10B.9C.8D.5【考点】HR:余弦定理.菁优网版权所有【专题】58:解三角形.【分析】利用二倍角的余弦函数公式化简已知的等式,求出cosA的值,再由a与c的值,利用余弦定理即可求出b的值.【解答】解:∵23cos2A+cos2A=23cos2A+2cos2A1=0﹣,即cos2A=,A为锐角,∴cosA=,又a=7,c=6,根据余弦定理得:a2=b2+c22bc•cosA﹣,即49=b2+36﹣b,解得:b=5或b=﹣(舍去),则b=5.故选:D.【点评】此题考查了余弦定理,二倍角的余弦函数公式,熟练掌握余弦定理是解本题的关键. 11.(5分)某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π【考点】L!:由三视图求面积、体积.菁优网版权所有【专题】16:压轴题;27:图表型.【分析】三视图复原的几何体是一个长方体与半个圆柱的组合体,依据三视图的数据,得出组合体长、宽、高,即可求出几何体的体积.【解答】解:三视图复原的几何体是一个长方体与半个圆柱的组合体,如图,其中长方体长、宽、高分别是:4,2,2,半个圆柱的底面半径为2,母线长为4.∴长方体的体积=4×2×2=16,半个圆柱的体积=×22×π×4=8π所以这个几何体的体积是16+8π;故选:A.【点评】本题考查了几何体的三视图及直观图的画法,三视图与直观图的关系,柱体体积计算公式,空间想象能力 12.(5分)已知函数f(x)=,若|f(x)|≥ax,则a的取值范围是( )A.(﹣∞,0]B.(﹣∞,1]C.[2﹣,1]D.[2﹣,0]【考点】7E:其他不等式的解法.菁优网版权所有【专题】16:压轴题;59:不等式的解法及应用.【分析】由函数图象的变换,结合基本初等函数的图象可作出函数y=|f(x)|的图象,和函数y=ax的图象,由导数求切线斜率可得l的斜率,进而数形结合可得a的范围.【解答】解:由题意可作出函数y=|f(x)|的图象,和函数y=ax的图象,由图象可知:函数y=ax的图象为过原点的直线,当直线介于l和x轴之间符合题意,直线l为曲线的切线,且此时函数y=|f(x)|在第二象限的部分解析式为y=x22x﹣,求其导数可得y=2x2′﹣,因为x≤0,故y′≤2﹣,故直线l的斜率为﹣2,故只需直线y=ax的斜率a介于﹣2与0之间即可,即a∈[2﹣,0]故选:D.【点评】本题考查其它不等式的解法,数形结合是解决问题的关键,属中档题. 二.填空题:本大题共四小题,每小题5分.13.(5分)已知两个单位向量,的夹角为60°,=t+(1t﹣).若•=0,则t= 2 .【考点】9H:平面向量的基本定理;9O:平面向量数量积的性质及其运算.菁优网版权所有【专题】5A:平面向量及应用.【分析】由于•=0,对式子=t+(1t﹣)两边与作数量积可得=0,经过化简即可得出.【解答】解:∵,,∴=0,∴tcos60°+1t=0﹣,∴1=0,解得t=2.故答案为2.【点评】熟练掌握向量的数量积运算是解题的关键. 14.(5分)设x,y满足约束条件,则z=2xy﹣的最大值为 3.【考点】7C:简单线性规划.菁优网版权所有【专题】59:不等式的解法及应用.【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=2xy﹣表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可.【解答】解:不等式组表示的平面区域如图所示,由得A(3,3),z=2xy﹣可转换成y=2xz﹣,z最大时,y值最小,即:当直线z=2xy﹣过点A(3,3)时,在y轴上截距最小,此时z取得最大值3.故答案为:3.【点评】本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题. 15.(5分)已知H是球O的直径AB上一点,AH:HB=1:2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为 .【考点】LG:球的体积和表面积.菁优网版权所有【专题】16:压轴题;5F:空间位置关系与距离.【分析】本题考查的知识点是球的表面积公式,设球的半径为R,根据题意知由与球心距离为R的平面截球所得的截面圆的面积是π,我们易求出截面圆的半径为1,根据球心距、截面圆半径、球半径构成直角三角形,满足勾股定理我们易求出该球的半径,进而求出球的表面积.【解答】解:设球的半径为R,∵AH:HB=1:2,∴平面α与球心的距离为R,∵α截球O所得截面的面积为π,∴d=R时,r=1,故由R2=r2+d2得R2=12+(R)2,∴R2=∴球的表面积S=4πR2=.故答案为:.【点评】若球的截面圆半径为r,球心距为d,球半径为R,则球心距、截面圆半径、球半径构成直角三角形,满足勾股定理,即R2=r2+d2 16.(5分)设当x=θ时,函数f(x)=sinx2cosx﹣取得最大值,则cosθ= ﹣ .【考点】GP:两角和与差的三角函数;H4:正弦函数的定义域和值域.菁优网版权所有【专题】16:压轴题;56:三角函数的求值.【分析】f(x)解析式提取,利用两角和与差的正弦函数公式化为一个角的正弦函数,由x=θ时,函数f(x)取得最大值,得到sinθ2cosθ=﹣,与sin2θ+cos2θ=1联立即可求出cosθ的值.【解答】解:f(x)=sinx2cosx=﹣(sinx﹣cosx)=sin(xα﹣)(其中cosα=,sinα=),∵x=θ时,函数f(x)取得最大值,∴sin(θα﹣)=1,即sinθ2cosθ=﹣,又sin2θ+cos2θ=1,联立得(2cosθ+)2+cos2θ=1,解得cosθ=﹣.故答案为:﹣【点评】此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键. 三.解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知等差数列{an}的前n项和Sn满足S3=0,S5=5﹣.(Ⅰ)求{an}的通项公式;(Ⅱ)求数列{}的前n项和.【考点】84:等差数列的通项公式;8E:数列的求和.菁优网版权所有【专题】54:等差数列与等比数列.【分析】(Ⅰ)设出等差数列{an}的首项和公差,直接由S3=0,S5=5﹣列方程组求出,然后代入等差数列的通项公式整理;(Ⅱ)把(Ⅰ)中求出的通项公式,代入数列{}的通项中进行列项整理,则利用裂项相消可求数列{}的前n项和.【解答】解:(Ⅰ)设数列{an}的首项为a1,公差为d,则.由已知可得,即,解得a1=1,d=1﹣,故{an}的通项公式为an=a1+(n1﹣)d=1+(n1﹣)•(﹣1)=2n﹣;(Ⅱ)由(Ⅰ)知.从而数列{}的前n项和Sn==.【点评】本题考查了等差数列的通项公式,考查了裂项相消法求数列的和,是中档题. 18.(12分)为了比较两种治疗失眠症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:服用A药的20位患者日平均增加的睡眠时间:0.61.22.71.52.81.82.22.33.23.52.52.61.22.71.52.93.03.12.32.4服用B药的20位患者日平均增加的睡眠时间:3.21.71.90.80.92.41.22.61.31.41.60.51.80.62.11.12.51.22.70.5(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?【考点】BA:茎叶图;BB:众数、中位数、平均数.菁优网版权所有【专题】5I:概率与统计.【分析】(Ⅰ)利用平均数的计算公式即可得出,据此即可判断出结论;(Ⅱ)利用已知数据和茎叶图的结构即可完成.【解答】解:(Ⅰ)设A药观测数据的平均数据的平均数为,设B药观测数据的平均数据的平均数为,则=×(0.6+1.2+2.7+1.5+2.8+1.8+2.2+2.3+3.2+3.5+2.5+2.6+1.2+2.7+1.5+2.9+3.0+3.1+2.3+2.4)=2.3.×(3.2+1.7+1.9+0.8+0.9+2.4+1.2+2.6+1.3+1.4+1.6+0.5+1.8+0.6+2.1+1.1+2.5+1.2+2.7+0.5)=1.6.由以上计算结果可知:.由此可看出A药的效果更好.(Ⅱ)根据两组数据得到下面茎叶图:从以上茎叶图可以看出,A药疗效的试验结果有的叶集中在2,3上.而B药疗效的试验结果由的叶集中在0,1上.由此可看出A药的疗效更好.【点评】熟练掌握平均数的计算公式和茎叶图的结果及其功能是解题的关键. 19.(12分)如图,三棱柱ABCA﹣1B1C1中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C;(Ⅱ)若AB=CB=2,A1C=,求三棱柱ABCA﹣1B1C1的体积.【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直.菁优网版权所有【专题】5F:空间位置关系与距离.【分析】(Ⅰ)由题目给出的边的关系,可想到去AB中点O,连结OC,OA1,可通过证明AB⊥平面OA1C得要证的结论;(Ⅱ)在三角形OCA1中,由勾股定理得到OA1⊥OC,再根据OA1⊥AB,得到OA1为三棱柱ABCA﹣1B1C1的高,利用已知给出的边的长度,直接利用棱柱体积公式求体积.【解答】(Ⅰ)证明:如图,取AB的中点O,连结OC,OA1,A1B.因为CA=CB,所以OC⊥AB.由于AB=AA1,,故△AA1B为等边三角形,所以OA1⊥AB.因为OC∩OA1=O,所以AB⊥平面OA1C.又A1C⊂平面OA1C,故AB⊥A1C;(Ⅱ)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,所以.又,则,故OA1⊥OC.因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABCA﹣1B1C1的高.又△ABC的面积,故三棱柱ABCA﹣1B1C1的体积.【点评】题主要考查了直线与平面垂直的性质,考查了棱柱的体积,考查空间想象能力、运算能力和推理论证能力,属于中档题. 20.(12分)已知函数f(x)=ex(ax+b)﹣x24x﹣,曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4.(Ⅰ)求a,b的值;(Ⅱ)讨论f(x)的单调性,并求f(x)的极大值.【考点】6D:利用导数研究函数的极值;6H:利用导数研究曲线上某点切线方程菁优网版权所有【专题】16:压轴题;53:导数的综合应用.【分析】(Ⅰ)求导函数,利用导数的几何意义及曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4,建立方程,即可求得a,b的值;(Ⅱ)利用导数的正负,可得f(x)的单调性,从而可求f(x)的极大值.【解答】解:(Ⅰ)∵f(x)=ex(ax+b)﹣x24x﹣,∴f′(x)=ex(ax+a+b)﹣2x4﹣,∵曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4∴f(0)=4,f′(0)=4∴b=4,a+b=8∴a=4,b=4;(Ⅱ)由(Ⅰ)知,f(x)=4ex(x+1)﹣x24x﹣,f′(x)=4ex(x+2)﹣2x﹣4=4(x+2)(ex﹣),令f′(x)=0,得x=ln2﹣或x=2﹣∴x∈(﹣∞,﹣2)或(﹣ln2,+∞)时,f′(x)>0;x∈(﹣2,﹣ln2)时,f′(x)<0∴f(x)的单调增区间是(﹣∞,﹣2),(﹣ln2,+∞),单调减区间是(﹣2,﹣ln2)当x=2﹣时,函数f(x)取得极大值,极大值为f(﹣2)=4(1e﹣2﹣).【点评】本题考查导数的几何意义,考查函数的单调性与极值,考查学生的计算能力,确定函数的解析式是关键. 21.(12分)已知圆M:(x+1)2+y2=1,圆N:(x1﹣)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.【考点】J3:轨迹方程;J9:直线与圆的位置关系.菁优网版权所有【专题】5B:直线与圆.【分析】(I)设动圆的半径为R,由已知动圆P与圆M外切并与圆N内切,可得|PM|+|PN|=R+1+(3R﹣)=4,而|NM|=2,由椭圆的定义可知:动点P的轨迹是以M,N为焦点,4为长轴长的椭圆,求出即可;(II)设曲线C上任意一点P(x,y),由于|PM|﹣|PN|=2R2﹣≤42=2﹣,所以R≤2,当且仅当⊙P的圆心为(2,0)R=2时,其半径最大,其方程为(x2﹣)2+y2=4.分①l的倾斜角为90°,此时l与y轴重合,可得|AB|.②若l的倾斜角不为90°,由于⊙M的半径1≠R,可知l与x轴不平行,设l与x轴的交点为Q,根据,可得Q(﹣4,0),所以可设l:y=k(x+4),与椭圆的方程联立,得到根与系数的关系利用弦长公式即可得出.【解答】解:(I)由圆M:(x+1)2+y2=1,可知圆心M(﹣1,0);圆N:(x1﹣)2+y2=9,圆心N(1,0),半径3.设动圆的半径为R,∵动圆P与圆M外切并与圆N内切,∴|PM|+|PN|=R+1+(3R﹣)=4,而|NM|=2,由椭圆的定义可知:动点P的轨迹是以M,N为焦点,4为长轴长的椭圆,∴a=2,c=1,b2=a2c﹣2=3.∴曲线C的方程为(x≠2﹣).(II)设曲线C上任意一点P(x,y),由于|PM|﹣|PN|=2R2﹣≤31=2﹣,所以R≤2,当且仅当⊙P的圆心为(2,0)R=2时,其半径最大,其方程为(x2﹣)2+y2=4.①l的倾斜角为90°,则l与y轴重合,可得|AB|=.②若l的倾斜角不为90°,由于⊙M的半径1≠R,可知l与x轴不平行,设l与x轴的交点为Q,则,可得Q(﹣4,0),所以可设l:y=k(x+4),由l于M相切可得:,解得.当时,联立,得到7x2+8x8=0﹣.∴,.∴|AB|===由于对称性可知:当时,也有|AB|=.综上可知:|AB|=或.【点评】本题综合考查了两圆的相切关系、直线与圆相切问题、椭圆的定义及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式等基础知识,需要较强的推理能力和计算能力及其分类讨论的思想方法. 请考生在第22、23、24三题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑。22.(10分)(选修41﹣:几何证明选讲)如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.(Ⅰ)证明:DB=DC;(Ⅱ)设圆的半径为1,BC=,延长CE交AB于点F,求△BCF外接圆的半径.【考点】NC:与圆有关的比例线段.菁优网版权所有【专题】5B:直线与圆.【分析】(I)连接DE交BC于点G,由弦切角定理可得∠ABE=∠BCE,由已知角平分线可得∠ABE=∠CBE,于是得到∠CBE=∠BCE,BE=CE.由已知DB⊥BE,可知DE为⊙O的直径,Rt△DBE≌Rt△DCE,利用三角形全等的性质即可得到DC=DB.(II)由(I)可知:DG是BC的垂直平分线,即可得到BG=.设DE的中点为O,连接BO,可得∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°.得到CF⊥BF.进而得到Rt△BCF的外接圆的半径=.【解答】(I)证明:连接DE交BC于点G.由弦切角定理可得∠ABE=∠BCE,而∠ABE=∠CBE,∴∠CBE=∠BCE,BE=CE.又∵DB⊥BE,∴DE为⊙O的直径,∠DCE=90°.∴△DBE≌△DCE,∴DC=DB.(II)由(I)可知:∠CDE=∠BDE,DB=DC.故DG是BC的垂直平分线,∴BG=.设DE的中点为O,连接BO,则∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°.∴CF⊥BF.∴Rt△BCF的外接圆的半径=.【点评】本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形全等、三角形的外接圆的半径等知识,需要较强的推理能力、分析问题和解决问题的能力. 23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.菁优网版权所有【专题】11:计算题;35:转化思想;4R:转化法;5S:坐标系和参数方程.【分析】(1)曲线C1的参数方程消去参数t,得到普通方程,再由,能求出C1的极坐标方程.(2)曲线C2的极坐标方程化为直角坐标方程,与C1的普通方程联立,求出C1与C2交点的直角坐标,由此能求出C1与C2交点的极坐标.【解答】解:(1)将,消去参数t,化为普通方程(x4﹣)2+(y﹣5)2=25,即C1:x2+y28x10y﹣﹣+16=0,将代入x2+y28x10y﹣﹣+16=0,得ρ28ρcosθ10ρsinθ﹣﹣+16=0.∴C1的极坐标方程为ρ28ρcosθ10ρsinθ﹣﹣+16=0.(2)∵曲线C2的极坐标方程为ρ=2sinθ.∴曲线C2的直角坐标方程为x2+y22y=0﹣,联立,解得或,∴C1与C2交点的极坐标为()和(2,).【点评】本题考查曲线极坐标方程的求法,考查两曲线交点的极坐标的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题. 24.已知函数f(x)=|2x1﹣|+|2x+a|,g(x)=x+3.(Ⅰ)当a=2﹣时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当x∈[﹣,]时,f(x)≤g(x),求a的取值范围.【考点】R5:绝对值不等式的解法.菁优网版权所有【分析】(Ⅰ)当a=2﹣时,求不等式f(x)<g(x)化为|2x1﹣|+|2x2﹣|x﹣3﹣<0.设y=|2x1﹣|+|2x2﹣|x3﹣﹣,画出函数y的图象,数形结合可得结论.(Ⅱ)不等式化即1+a≤x+3,故x≥a2﹣对x∈[﹣,]都成立,分析可得﹣≥a2﹣,由此解得a的取值范围.【解答】解:(Ⅰ)当a=2﹣时,求不等式f(x)<g(x)化为|2x1﹣|+|2x2﹣|x3﹣﹣<0.设y=|2x1﹣|+|2x2﹣|x3﹣﹣,则y=,它的图象如图所示:结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).(Ⅱ)设a>﹣1,且当x∈[﹣,]时,f(x)=1+a,不等式化为1+a≤x+3,故x≥a2﹣对x∈[﹣,]都成立.故﹣≥a2﹣,解得a≤,故a的取值范围为(﹣1,].【点评】本题考查绝对值不等式的解法与绝对值不等式的性质,关键是利用零点分段讨论法分析函数的解析式.










 青岛版六年级数学上册《归类培优测试卷3图形与几何和统计与概率》+答案
青岛版六年级数学上册《归类培优测试卷3图形与几何和统计与概率》+答案 2015年山东省高考数学(理科)模拟冲刺卷(一)+答案
2015年山东省高考数学(理科)模拟冲刺卷(一)+答案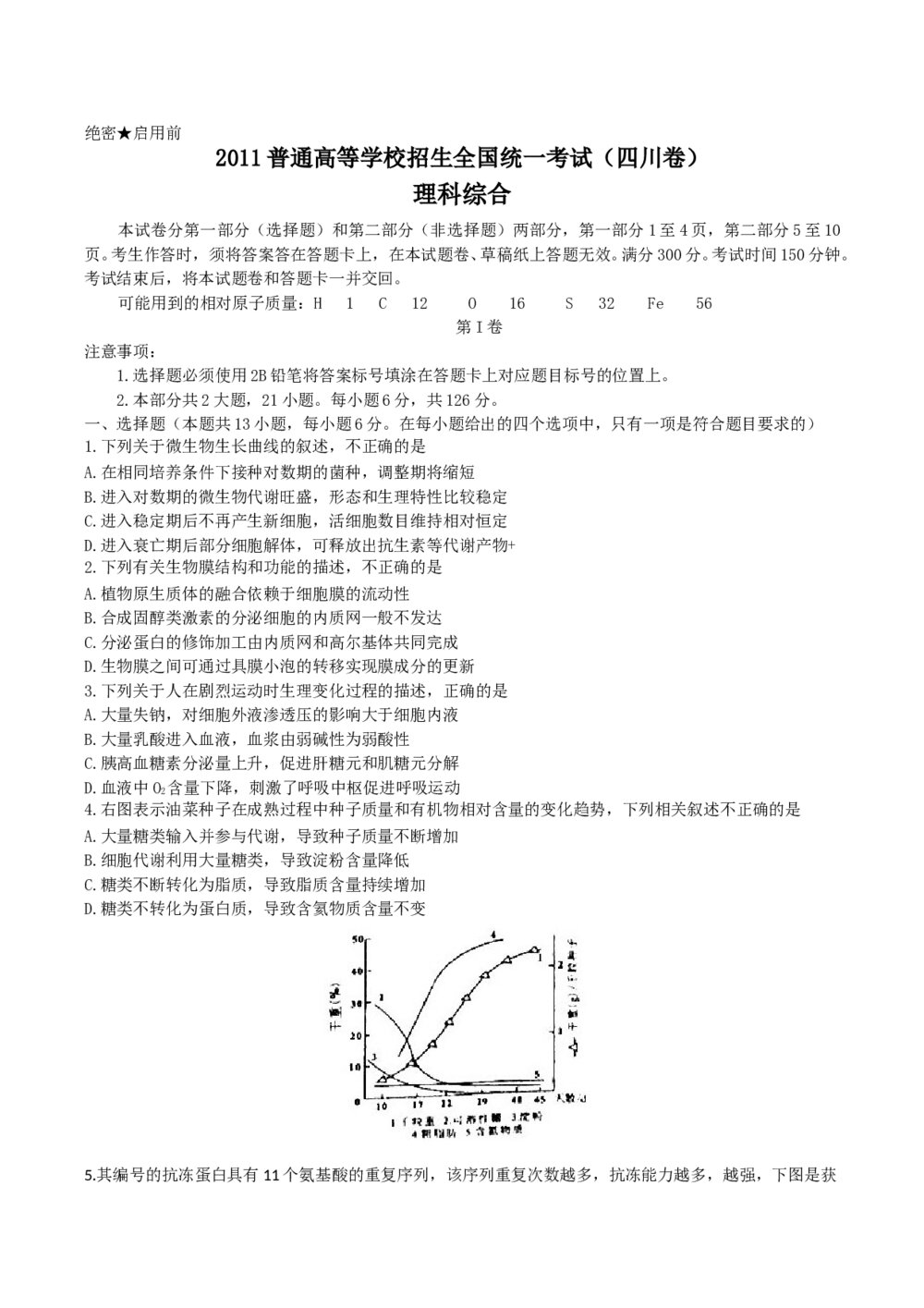 2011年四川高考理科综合试题卷word版
2011年四川高考理科综合试题卷word版 2005年高考理科数学·上海卷试题+参考答案(word版)
2005年高考理科数学·上海卷试题+参考答案(word版) 2013年上海高考数学(理科)真题试卷word版+答案解析
2013年上海高考数学(理科)真题试卷word版+答案解析 六年级上册数学四单元考试卷word版
六年级上册数学四单元考试卷word版