









试读已结束,还剩20页未读,您可下载完整版后进行离线阅读
《2017年全国统一高考数学试卷(文科)(新课标ⅲ)+参考答案解析》是由用户上传到老师板报网,本为文库资料,大小为387.5 KB,总共有30页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 30页
- 387.5 KB
- VIP模板
- doc
- 数字产品不支持退货
2017年全国统一高考数学试卷(文科)(新课标Ⅲ)一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )A.1B.2C.3D.42.(5分)复平面内表示复数z=i(﹣2+i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)已知sinαcosα=﹣,则sin2α=( )A.﹣B.﹣C.D.5.(5分)设x,y满足约束条件则z=xy﹣的取值范围是( )A.[3﹣,0]B.[3﹣,2]C.[0,2]D.[0,3]6.(5分)函数f(x)=sin(x+)+cos(x﹣)的最大值为( )A.B.1C.D.7.(5分)函数y=1+x+的部分图象大致为( )A.B.C.D.8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5B.4C.3D.29.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.C.D.10.(5分)在正方体ABCDA﹣1B1C1D1中,E为棱CD的中点,则( )A.A1E⊥DC1B.A1E⊥BDC.A1E⊥BC1D.A1E⊥AC11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bxay﹣+2ab=0相切,则C的离心率为( )A.B.C.D.12.(5分)已知函数f(x)=x22x﹣+a(ex1﹣+ex﹣+1)有唯一零点,则a=( )A.﹣B.C.D.1 二、填空题13.(5分)已知向量=(﹣2,3),=(3,m),且,则m=.14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a=.15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=,c=3,则A= .16.(5分)设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是 . 三、解答题17.(12分)设数列{an}满足a1+3a2+…+(2n1﹣)an=2n.(1)求{an}的通项公式;(2)求数列{}的前n项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx2﹣与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤﹣﹣2. [选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径. [选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣|x2﹣|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2x﹣+m的解集非空,求m的取值范围. 2017年全国统一高考数学试卷(文科)(新课标Ⅲ)参考答案与试题解析 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )A.1B.2C.3D.4【考点】1E:交集及其运算.菁优网版权所有【专题】11:计算题;37:集合思想;4O:定义法;5J:集合.【分析】利用交集定义先求出A∩B,由此能求出A∩B中元素的个数.【解答】解:∵集合A={1,2,3,4},B={2,4,6,8},∴A∩B={2,4},∴A∩B中元素的个数为2.故选:B.【点评】本题考查交集中元素个数的求法,是基础题,解题时要认真审题,注意交集定义的合理运用. 2.(5分)复平面内表示复数z=i(﹣2+i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限【考点】A4:复数的代数表示法及其几何意义.菁优网版权所有【专题】35:转化思想;5N:数系的扩充和复数.【分析】利用复数的运算法则、几何意义即可得出.【解答】解:z=i(﹣2+i)=2i1﹣﹣对应的点(﹣1,﹣2)位于第三象限.故选:C.【点评】本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题. 3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳【考点】2K:命题的真假判断与应用;B9:频率分布折线图、密度曲线.菁优网版权所有【专题】27:图表型;2A:探究型;5I:概率与统计.【分析】根据已知中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,逐一分析给定四个结论的正误,可得答案.【解答】解:由已有中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据可得:月接待游客量逐月有增有减,故A错误;年接待游客量逐年增加,故B正确;各年的月接待游客量高峰期大致在7,8月,故C正确;各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确;故选:A.【点评】本题考查的知识点是数据的分析,命题的真假判断与应用,难度不大,属于基础题. 4.(5分)已知sinαcosα=﹣,则sin2α=( )A.﹣B.﹣C.D.【考点】GS:二倍角的三角函数.菁优网版权所有【专题】11:计算题;35:转化思想;4O:定义法;56:三角函数的求值.【分析】由条件,两边平方,根据二倍角公式和平方关系即可求出.【解答】解:∵sinαcosα=﹣,∴(sinαcosα﹣)2=12sinαcosα=1sin2α=﹣﹣,∴sin2α=﹣,故选:A.【点评】本题考查了二倍角公式,属于基础题. 5.(5分)设x,y满足约束条件则z=xy﹣的取值范围是( )A.[3﹣,0]B.[3﹣,2]C.[0,2]D.[0,3]【考点】7C:简单线性规划.菁优网版权所有【专题】11:计算题;31:数形结合;35:转化思想;5T:不等式.【分析】画出约束条件的可行域,利用目标函数的最优解求解目标函数的范围即可.【解答】解:x,y满足约束条件的可行域如图:目标函数z=xy﹣,经过可行域的A,B时,目标函数取得最值,由解得A(0,3),由解得B(2,0),目标函数的最大值为:2,最小值为:﹣3,目标函数的取值范围:[3﹣,2].故选:B.【点评】本题考查线性规划的简单应用,目标函数的最优解以及可行域的作法是解题的关键. 6.(5分)函数f(x)=sin(x+)+cos(x﹣)的最大值为( )A.B.1C.D.【考点】HW:三角函数的最值.菁优网版权所有【专题】11:计算题;35:转化思想;49:综合法;57:三角函数的图像与性质【分析】利用诱导公式化简函数的解析式,通过正弦函数的最值求解即可.【解答】解:函数f(x)=sin(x+)+cos(x﹣)=sin(x+)+cos(﹣x+)=sin(x+)+sin(x+)=sin(x+).故选:A.【点评】本题考查诱导公式的应用,三角函数的最值,正弦函数的有界性,考查计算能力. 7.(5分)函数y=1+x+的部分图象大致为( )A.B.C.D.【考点】3A:函数的图象与图象的变换.菁优网版权所有【专题】11:计算题;31:数形结合;35:转化思想;51:函数的性质及应用.【分析】通过函数的解析式,利用函数的奇偶性的性质,函数的图象经过的特殊点判断函数的图象即可.【解答】解:函数y=1+x+,可知:f(x)=x+是奇函数,所以函数的图象关于原点对称,则函数y=1+x+的图象关于(0,1)对称,当x→0+,f(x)>0,排除A、C,当x=π时,y=1+π,排除B.故选:D.【点评】本题考查函数的图象的判断,函数的奇偶性以及特殊点是常用方法. 8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5B.4C.3D.2【考点】EF:程序框图.菁优网版权所有【专题】11:计算题;39:运动思想;49:综合法;5K:算法和程序框图.【分析】通过模拟程序,可得到S的取值情况,进而可得结论.【解答】解:由题可知初始值t=1,M=100,S=0,要使输出S的值小于91,应满足“t≤N”,则进入循环体,从而S=100,M=10﹣,t=2,要使输出S的值小于91,应接着满足“t≤N”,则进入循环体,从而S=90,M=1,t=3,要使输出S的值小于91,应不满足“t≤N”,跳出循环体,此时N的最小值为2,故选:D.【点评】本题考查程序框图,判断出什么时候跳出循环体是解决本题的关键,注意解题方法的积累,属于中档题. 9.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.C.D.【考点】LF:棱柱、棱锥、棱台的体积;LR:球内接多面体.菁优网版权所有【专题】11:计算题;34:方程思想;4O:定义法;5Q:立体几何.【分析】推导出该圆柱底面圆周半径r==,由此能求出该圆柱的体积.【解答】解:∵圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,∴该圆柱底面圆周半径r==,∴该圆柱的体积:V=Sh==.故选:B.【点评】本题考查面圆柱的体积的求法,考查圆柱、球等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想,是中档题. 10.(5分)在正方体ABCDA﹣1B1C1D1中,E为棱CD的中点,则( )A.A1E⊥DC1B.A1E⊥BDC.A1E⊥BC1D.A1E⊥AC【考点】LO:空间中直线与直线之间的位置关系.菁优网版权所有【专题】11:计算题;31:数形结合;41:向量法;5G:空间角.【分析】法一:连B1C,推导出BC1⊥B1C,A1B1⊥BC1,从而BC1⊥平面A1ECB1,由此得到A1E⊥BC1.法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出结果.【解答】解:法一:连B1C,由题意得BC1⊥B1C,∵A1B1⊥平面B1BCC1,且BC1⊂平面B1BCC1,∴A1B1⊥BC1,∵A1B1∩B1C=B1,∴BC1⊥平面A1ECB1,∵A1E⊂平面A1ECB1,∴A1E⊥BC1.故选:C.法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCDA﹣1B1C1D1中棱长为2,则A1(2,0,2),E(0,1,0),B(2,2,0),D(0,0,0),C1(0,2,2),A(2,0,0),C(0,2,0),=(﹣2,1,﹣2),=(0,2,2),=(﹣2,﹣2,0),=(﹣2,0,2),=(﹣2,2,0),∵•=2﹣,=2,=0,=6,∴A1E⊥BC1.故选:C.【点评】本题考查线线垂直的判断,是中档题,解题时要认真审题,注意向量法的合理运用. 11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bxay﹣+2ab=0相切,则C的离心率为( )A.B.C.D.【考点】K4:椭圆的性质.菁优网版权所有【专题】34:方程思想;5B:直线与圆;5D:圆锥曲线的定义、性质与方程.【分析】以线段A1A2为直径的圆与直线bxay﹣+2ab=0相切,可得原点到直线的距离=a,化简即可得出.【解答】解:以线段A1A2为直径的圆与直线bxay﹣+2ab=0相切,∴原点到直线的距离=a,化为:a2=3b2.∴椭圆C的离心率e===.故选:A.【点评】本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题. 12.(5分)已知函数f(x)=x22x﹣+a(ex1﹣+ex﹣+1)有唯一零点,则a=( )A.﹣B.C.D.1【考点】52:函数零点的判定定理.菁优网版权所有【专题】11:计算题;33:函数思想;49:综合法;51:函数的性质及应用.【分析】通过转化可知问题等价于函数y=1﹣(x1﹣)2的图象与y=a(ex1﹣+)的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.【解答】解:因为f(x)=x22x﹣+a(ex1﹣+ex﹣+1)=1﹣+(x1﹣)2+a(ex1﹣+)=0,所以函数f(x)有唯一零点等价于方程1﹣(x1﹣)2=a(ex1﹣+)有唯一解,等价于函数y=1﹣(x1﹣)2的图象与y=a(ex1﹣+)的图象只有一个交点.①当a=0时,f(x)=x22x﹣≥1﹣,此时有两个零点,矛盾;②当a<0时,由于y=1﹣(x1﹣)2在(﹣∞,1)上递增、在(1,+∞)上递减,且y=a(ex1﹣+)在(﹣∞,1)上递增、在(1,+∞)上递减,所以函数y=1﹣(x1﹣)2的图象的最高点为A(1,1),y=a(ex1﹣+)的图象的最高点为B(1,2a),由于2a<0<1,此时函数y=1﹣(x1﹣)2的图象与y=a(ex1﹣+)的图象有两个交点,矛盾;③当a>0时,由于y=1﹣(x1﹣)2在(﹣∞,1)上递增、在(1,+∞)上递减,且y=a(ex1﹣+)在(﹣∞,1)上递减、在(1,+∞)上递增,所以函数y=1﹣(x1﹣)2的图象的最高点为A(1,1),y=a(ex1﹣+)的图象的最低点为B(1,2a),由题可知点A与点B重合时满足条件,即2a=1,即a=,符合条件;综上所述,a=,故选:C.【点评】本题考查函数零点的判定定理,考查函数的单调性,考查运算求解能力考查数形结合能力,考查转化与化归思想,考查分类讨论的思想,注意解题方法的积累,属于难题. 二、填空题13.(5分)已知向量=(﹣2,3),=(3,m),且,则m= 2.【考点】9T:数量积判断两个平面向量的垂直关系.菁优网版权所有【专题】11:计算题;34:方程思想;4O:定义法;5A:平面向量及应用.【分析】利用平面向量数量积坐标运算法则和向量垂直的性质求解.【解答】解:∵向量=(﹣2,3),=(3,m),且,∴=6﹣+3m=0,解得m=2.故答案为:2.【点评】本题考查实数值的求法,是基础题,解题时要认真审题,注意平面向量数量积坐标运算法则和向量垂直的性质的合理运用. 14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a= 5.【考点】KC:双曲线的性质.菁优网版权所有【专题】11:计算题;35:转化思想;5D:圆锥曲线的定义、性质与方程.【分析】利用双曲线方程,求出渐近线方程,求解a即可.【解答】解:双曲线(a>0)的一条渐近线方程为y=x,可得,解得a=5.故答案为:5.【点评】本题考查双曲线的简单性质的应用,考查计算能力. 15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=,c=3,则A= 75° .【考点】HP:正弦定理;HR:余弦定理.菁优网版权所有【专题】11:计算题;35:转化思想;4O:定义法;58:解三角形.【分析】根据正弦定理和三角形的内角和计算即可【解答】解:根据正弦定理可得=,C=60°,b=,c=3,∴sinB==,∵b<c,∴B=45°,∴A=180°BC=180°45°60°=75°﹣﹣﹣﹣,故答案为:75°.【点评】本题考查了三角形的内角和以及正弦定理,属于基础题 16.(5分)设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是 (,+∞) .【考点】3T:函数的值.菁优网版权所有【专题】32:分类讨论;4R:转化法;51:函数的性质及应用.【分析】根据分段函数的表达式,分别讨论x的取值范围,进行求解即可.【解答】解:若x≤0,则x﹣≤﹣,则f(x)+f(x﹣)>1等价为x+1+x﹣+1>1,即2x>﹣,则x>,此时<x≤0,当x>0时,f(x)=2x>1,x﹣>﹣,当x﹣>0即x>时,满足f(x)+f(x﹣)>1恒成立,当0≥x﹣>﹣,即≥x>0时,f(x﹣)=x﹣+1=x+,此时f(x)+f(x﹣)>1恒成立,综上x>,故答案为:(,+∞).【点评】本题主要考查不等式的求解,结合分段函数的不等式,利用分类讨论的数学思想进行求解是解决本题的关键. 三、解答题17.(12分)设数列{an}满足a1+3a2+…+(2n1﹣)an=2n.(1)求{an}的通项公式;(2)求数列{}的前n项和.【考点】8E:数列的求和;8H:数列递推式.菁优网版权所有【专题】34:方程思想;35:转化思想;54:等差数列与等比数列.【分析】(1)利用数列递推关系即可得出.(2)==﹣.利用裂项求和方法即可得出.【解答】解:(1)数列{an}满足a1+3a2+…+(2n1﹣)an=2n.n≥2时,a1+3a2+…+(2n3﹣)an1﹣=2(n1﹣).∴(2n1﹣)an=2.∴an=.当n=1时,a1=2,上式也成立.∴an=.(2)==﹣.∴数列{}的前n项和=++…+=1﹣=.【点评】本题考查了数列递推关系、裂项求和方法,考查了推理能力与计算能力属于中档题. 18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.【考点】CB:古典概型及其概率计算公式;CH:离散型随机变量的期望与方差.菁优网版权所有【专题】11:计算题;35:转化思想;49:综合法;5I:概率与统计.【分析】(1)由前三年六月份各天的最高气温数据,求出最高气温位于区间[20,25)和最高气温低于20的天数,由此能求出六月份这种酸奶一天的需求量不超过300瓶的概率.(2)当温度大于等于25°C时,需求量为500,求出Y=900元;当温度在[20,25)°C时,需求量为300,求出Y=300元;当温度低于20°C时,需求量为200,求出Y=100﹣元,从而当温度大于等于20时,Y>0,由此能估计估计Y大于零的概率.【解答】解:(1)由前三年六月份各天的最高气温数据,得到最高气温位于区间[20,25)和最高气温低于20的天数为2+16+36=54,根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶,如果最高气温位于区间[20,25),需求量为300瓶,如果最高气温低于20,需求量为200瓶,∴六月份这种酸奶一天的需求量不超过300瓶的概率p==.(2)当温度大于等于25°C时,需求量为500,Y=450×2=900元,当温度在[20,25)°C时,需求量为300,Y=300×2﹣(450300﹣)×2=300元,当温度低于20°C时,需求量为200,Y=400﹣(450200﹣)×2=100﹣元,当温度大于等于20时,Y>0,由前三年六月份各天的最高气温数据,得当温度大于等于20°C的天数有:90﹣(2+16)=72,∴估计Y大于零的概率P=.【点评】本题考查概率的求法,考查利润的所有可能取值的求法,考查函数、古典概型等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题. 19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直.菁优网版权所有【专题】11:计算题;31:数形结合;41:向量法;5F:空间位置关系与距离.【分析】(1)取AC中点O,连结DO、BO,推导出DO⊥AC,BO⊥AC,从而AC⊥平面BDO,由此能证明AC⊥BD.(2)法一:连结OE,设AD=CD=,则OC=OA=1,由余弦定理求出BE=1,由BE=ED,四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,S△DCE=S△BCE,由此能求出四面体ABCE与四面体ACDE的体积比.法二:设AD=CD=,则AC=AB=BC=BD=2,AO=CO=DO=1,BO=,推导出BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,由AE⊥EC,求出DE=BE,由此能求出四面体ABCE与四面体ACDE的体积比.【解答】证明:(1)取AC中点O,连结DO、BO,∵△ABC是正三角形,AD=CD,∴DO⊥AC,BO⊥AC,∵DO∩BO=O,∴AC⊥平面BDO,∵BD⊂平面BDO,∴AC⊥BD.解:(2)法一:连结OE,由(1)知AC⊥平面OBD,∵OE⊂平面OBD,∴OE⊥AC,设AD=CD=,则OC=OA=1,EC=EA,∵AE⊥CE,AC=2,∴EC2+EA2=AC2,∴EC=EA==CD,∴E是线段AC垂直平分线上的点,∴EC=EA=CD=,由余弦定理得:cos∠CBD==,即,解得BE=1或BE=2,∵BE<<BD=2,∴BE=1,∴BE=ED,∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,∵BE=ED,∴S△DCE=S△BCE,∴四面体ABCE与四面体ACDE的体积比为1.法二:设AD=CD=,则AC=AB=BC=BD=2,AO=CO=DO=1,∴BO==,∴BO2+DO2=BD2,∴BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,则C(﹣1,0,0),D(0,0,1),B(0,,0),A(1,0,0),设E(a,b,c),,(0≤λ≤1),则(a,b,c1﹣)=λ(0,,﹣1),解得E(0,,1λ﹣),∴=(1,),=(﹣1,),∵AE⊥EC,∴=1﹣+3λ2+(1λ﹣)2=0,由λ∈[0,1],解得,∴DE=BE,∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,∵DE=BE,∴S△DCE=S△BCE,∴四面体ABCE与四面体ACDE的体积比为1.【点评】本题考查线线垂直的证明,考查两个四面体的体积之比的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题. 20.(12分)在直角坐标系xOy中,曲线y=x2+mx2﹣与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.【考点】KJ:圆与圆锥曲线的综合.菁优网版权所有【专题】34:方程思想;43:待定系数法;5B:直线与圆.【分析】(1)设曲线y=x2+mx2﹣与x轴交于A(x1,0),B(x2,0),运用韦达定理,再假设AC⊥BC,运用直线的斜率之积为﹣1,即可判断是否存在这样的情况;(2)设过A、B、C三点的圆的方程为x2+y2+Dx+Ey+F=0(D2+E24F﹣>0),由题意可得D=m,F=2﹣,代入(0,1),可得E=1,再令x=0,即可得到圆在y轴的交点,进而得到弦长为定值.【解答】解:(1)曲线y=x2+mx2﹣与x轴交于A、B两点,可设A(x1,0),B(x2,0),由韦达定理可得x1x2=2﹣,若AC⊥BC,则kAC•kBC=1﹣,即有•=1﹣,即为x1x2=1﹣这与x1x2=2﹣矛盾,故不出现AC⊥BC的情况;(2)证明:设过A、B、C三点的圆的方程为x2+y2+Dx+Ey+F=0(D2+E24F﹣>0),由题意可得y=0时,x2+Dx+F=0与x2+mx2=0﹣等价,可得D=m,F=2﹣,圆的方程即为x2+y2+mx+Ey2=0﹣,由圆过C(0,1),可得0+1+0+E2=0﹣,可得E=1,则圆的方程即为x2+y2+mx+y2=0﹣,另解:设过A、B、C三点的圆在y轴上的交点为H(0,d),则由相交弦定理可得|OA|•|OB|=|OC|•|OH|,即有2=|OH|,再令x=0,可得y2+y2=0﹣,解得y=1或﹣2.即有圆与y轴的交点为(0,1),(0,﹣2),则过A、B、C三点的圆在y轴上截得的弦长为定值3.【点评】本题考查直线与圆的方程的求法,注意运用韦达定理和直线的斜率公式以及待定系数法,考查方程思想和化简整理的运算能力,属于中档题. 21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤﹣﹣2.【考点】6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.菁优网版权所有【专题】11:计算题;32:分类讨论;48:分析法;53:导数的综合应用.【分析】(1)题干求导可知f′(x)=(x>0),分a=0、a>0、a<0三种情况讨论f′(x)与0的大小关系可得结论;(2)通过(1)可知f(x)max=f(﹣)=1ln2﹣﹣﹣+ln(﹣),进而转化可知问题转化为证明:当t>0时﹣t+lnt≤1﹣+ln2.进而令g(t)=﹣t+lnt,利用导数求出y=g(t)的最大值即可.【解答】(1)解:因为f(x)=lnx+ax2+(2a+1)x,求导f′(x)=+2ax+(2a+1)==,(x>0),①当a=0时,f′(x)=+1>0恒成立,此时y=f(x)在(0,+∞)上单调递增;②当a>0,由于x>0,所以(2ax+1)(x+1)>0恒成立,此时y=f(x)在(0,+∞)上单调递增;③当a<0时,令f′(x)=0,解得:x=﹣.因为当x∈(0,﹣)f′(x)>0、当x∈(﹣,+∞)f′(x)<0,所以y=f(x)在(0,﹣)上单调递增、在(﹣,+∞)上单调递减.综上可知:当a≥0时f(x)在(0,+∞)上单调递增,当a<0时,f(x)在(0,﹣)上单调递增、在(﹣,+∞)上单调递减;(2)证明:由(1)可知:当a<0时f(x)在(0,﹣)上单调递增、在(﹣,+∞)上单调递减,所以当x=﹣时函数y=f(x)取最大值f(x)max=f(﹣)=1ln2﹣﹣﹣+ln(﹣).从而要证f(x)≤﹣﹣2,即证f(﹣)≤﹣﹣2,即证﹣1ln2﹣﹣+ln(﹣)≤﹣﹣2,即证﹣(﹣)+ln(﹣)≤﹣1+ln2.令t=﹣,则t>0,问题转化为证明:﹣t+lnt≤1﹣+ln2.…(*)令g(t)=﹣t+lnt,则g′(t)=﹣+,令g′(t)=0可知t=2,则当0<t<2时g′(t)>0,当t>2时g′(t)<0,所以y=g(t)在(0,2)上单调递增、在(2,+∞)上单调递减,即g(t)≤g(2)=﹣×2+ln2=1﹣+ln2,即(*)式成立,所以当a<0时,f(x)≤﹣﹣2成立.【点评】本题考查利用导数研究函数的单调性,考查分类讨论的思想,考查转化能力,考查运算求解能力,注意解题方法的积累,属于中档题. [选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径.【考点】QH:参数方程化成普通方程.菁优网版权所有【专题】34:方程思想;4Q:参数法;4R:转化法;5S:坐标系和参数方程.【分析】解:(1)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x2﹣)①与x=2﹣+ky②;联立①②,消去k可得C的普通方程为x2y﹣2=4;(2)将l3的极坐标方程为ρ(cosθ+sinθ)﹣=0化为普通方程:x+y﹣=0,再与曲线C的方程联立,可得,即可求得l3与C的交点M的极径为ρ=.【解答】解:(1)∵直线l1的参数方程为,(t为参数),∴消掉参数t得:直线l1的普通方程为:y=k(x2﹣)①;又直线l2的参数方程为,(m为参数),同理可得,直线l2的普通方程为:x=2﹣+ky②;联立①②,消去k得:x2y﹣2=4,即C的普通方程为x2y﹣2=4(x≠2且y≠0);(2)∵l3的极坐标方程为ρ(cosθ+sinθ)﹣=0,∴其普通方程为:x+y﹣=0,联立得:,∴ρ2=x2+y2=+=5.∴l3与C的交点M的极径为ρ=.【点评】本题考查参数方程与极坐标方程化普通方程,考查函数与方程思想与等价转化思想的运用,属于中档题. [选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣|x2﹣|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2x﹣+m的解集非空,求m的取值范围.【考点】R4:绝对值三角不等式;R5:绝对值不等式的解法.菁优网版权所有【专题】32:分类讨论;33:函数思想;4C:分类法;4R:转化法;51:函数的性质及应用;5T:不等式.【分析】(1)由于f(x)=|x+1|﹣|x2﹣|=,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;(2)依题意可得m≤[f(x)﹣x2+x]max,设g(x)=f(x)﹣x2+x,分x≤1、﹣1<x<2、x≥2三类讨论,可求得g(x)max=,从而可得m的取值范围.【解答】解:(1)∵f(x)=|x+1|﹣|x2﹣|=,f(x)≥1,∴当﹣1≤x≤2时,2x1﹣≥1,解得1≤x≤2;当x>2时,3≥1恒成立,故x>2;综上,不等式f(x)≥1的解集为{x|x≥1}.(2)原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,即m≤[f(x)﹣x2+x]max,设g(x)=f(x)﹣x2+x.由(1)知,g(x)=,当x≤1﹣时,g(x)=x﹣2+x3﹣,其开口向下,对称轴方程为x=>﹣1,∴g(x)≤g(﹣1)=113=5﹣﹣﹣﹣;当﹣1<x<2时,g(x)=x﹣2+3x1﹣,其开口向下,对称轴方程为x=∈(﹣1,2),∴g(x)≤g()=﹣+1=﹣;当x≥2时,g(x)=x﹣2+x+3,其开口向下,对称轴方程为x=<2,∴g(x)≤g(2)=4﹣+2+3=1;综上,g(x)max=,∴m的取值范围为(﹣∞,].【点评】本题考查绝对值不等式的解法,去掉绝对值符号是解决问题的关键,突出考查分类讨论思想与等价转化思想、函数与方程思想的综合运用,属于难题.










 2021年上海市夏季高考数学试卷(数学上海试卷)
2021年上海市夏季高考数学试卷(数学上海试卷) 一年级上册数学期末试卷word
一年级上册数学期末试卷word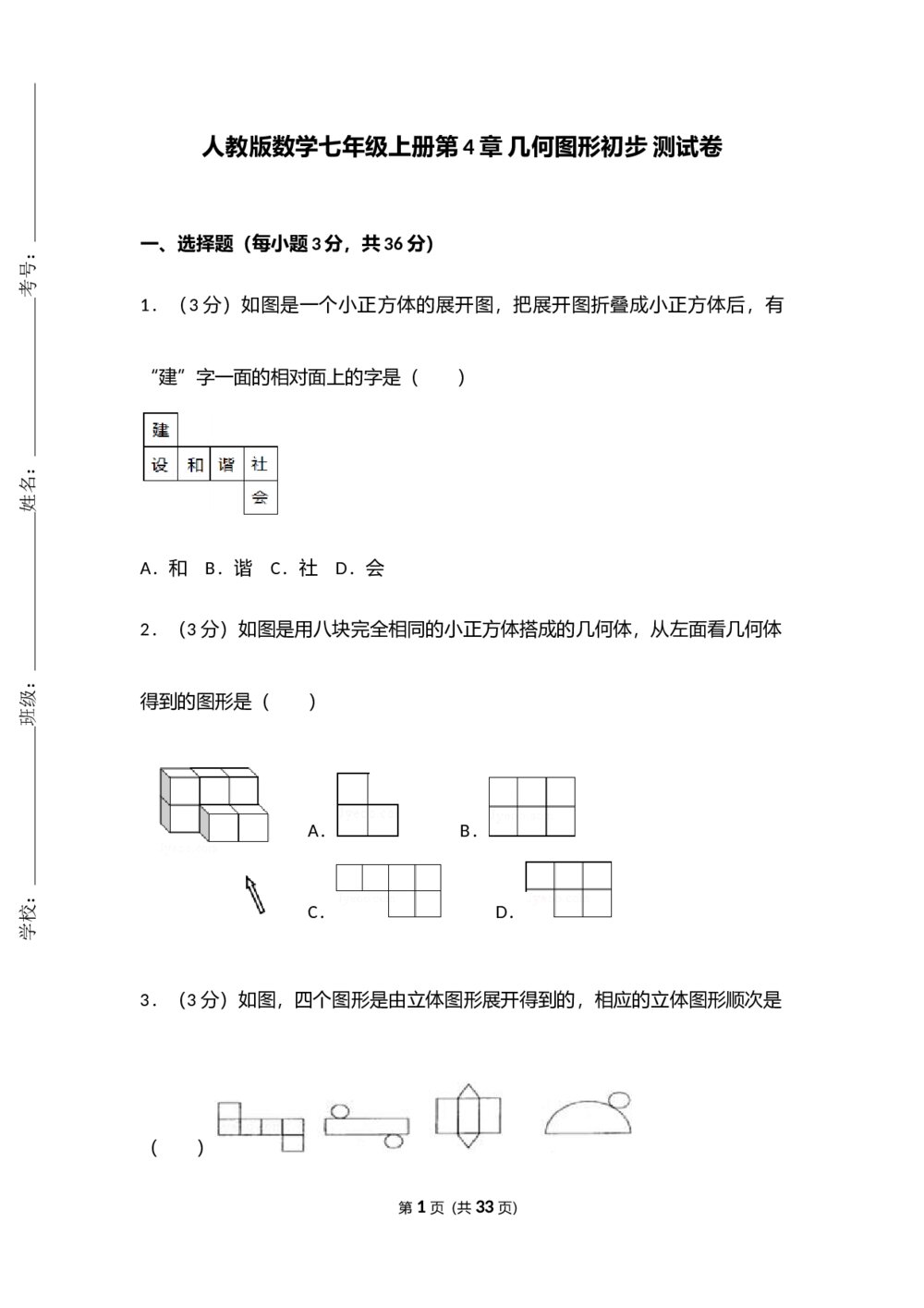 人教版七年级数学上册《第4章 几何图形初步》测试卷(Word版+含参考答案)
人教版七年级数学上册《第4章 几何图形初步》测试卷(Word版+含参考答案) 高考试题(湖南卷)--数学文科+(答案解析版)
高考试题(湖南卷)--数学文科+(答案解析版) 2020年高考真题数学试卷(理科)(新课标Ⅱ)(原卷版))+(答案解析)
2020年高考真题数学试卷(理科)(新课标Ⅱ)(原卷版))+(答案解析) 2015龙岩市高中毕业班质检数学(文科)试题+答案
2015龙岩市高中毕业班质检数学(文科)试题+答案